多項式フィッティングのワナ

Tag

# 解説

preferred

今回は新しい試みとして、かわいい柴犬の画像によっていろいろなことをごまかすことにチャレンジしています。なお、画像はflickrからCCライセンスのものをお借りしております。画像をクリックするともっと大きいのが見れるよ。

さて、本題に移りましょう。今日のテーマは多項式フィッティングです。より正確には、多項式フィッティングに関して、私がいくつかの落とし穴にはまった記録です。

多項式フィッティングというと、観測されたデータから項の係数を決める問題です。

もう少し具体的に書くと、

\(f(x) = w_0 + w_1 x + w_2 x^2 + w_3 x^3 \ldots\)

の\(w_0, w_1, \ldots\)の具体的な値をどう決めれば得られたデータに近い曲線が得られるか、というような問題です。ただし、観測したデータには必ずノイズが乗るものなので、誤差が0になるような曲線を作ればそれでよし、という問題ではありません。

そこで、\(f(x)\)と測定値の差の二乗を最小化する \(w_0, w_1, \ldots\) を求めることを目標とします。数式で書くと\(\sum_i \{y_i – f(x_i)\}^2\)を最小化するような \(w_0, w_1, \ldots\) を求めることになります。

\(\sum_i \{y_i – f(x_i)\}^2\)を\(w_0, w_1, \ldots\) で微分したものをそれぞれ0とすると、\(|\textbf{w}|\) 個の数の方程式ができます。\(\textbf{x}_i\) を並べたものを\(\textbf{X}\)とし、\(y_i\)を並べたものを\(\textbf{y}\)とした時、方程式は以下のように書けます。

\(\textbf{X}^{\top} \textbf{X} \textbf{w}^{\top} = \textbf{X}^{\top} \textbf{y}^{\top}\)

さて、問題は\(f(x)\)の重みを学習することですから、最小二乗法を使わずとも、Support Vector Regressionなどで何とかなりそうな気がします。という訳で、実際にFOBOSでSupport Vector Regressionの目的関数を最小化するコードを書いてみましたが、これがまず失敗その1です。まったくうまくいきませんでした。

この原因は、入力ベクトルの値の幅がとても大きなことです。例えば、x=2の時、x^2の項は4になりますが、x^16の項は2^16 = 65536が入力になるわけです。FOBOSのパラメーター更新では勾配を使いますが、x^2の項とx^16の項では勾配の値が違いすぎます。要するに、低次の項の影響が小さくなりすぎてしまいます。

これではサポートベクターマシンはうまく動作しませんので、入力をスケーリングして、いい感じに入力値の値が同じぐらいの範囲になるようにしなければなりません。しかしスケーリングはめんどくさい。という訳で、サポートベクター回帰のコードは捨てました。

余談ですが、スケーリングなどの入力データの正規化については、Quoraのこのトピックがとても参考になります。

という訳で、まじめな最小二乗法にトライしてみました。

def phi(x):
    r = []
    for i in range(0, N+1):
        r.append(x ** i)
    return r

def est(xv, yv):
    a = []
    for x in xv:
        a.append(phi(x))
    a = np.matrix(a)
    b = np.array(yv)

    A = a.T * a

    B = a.T * np.matrix(b).T
    w = np.linalg.solve(A, B)
    return w

xv, yvは多項式のデータが入ったものです。\(y = x^2\)だとしたら、xv = [0,1,2,3,4,5], yv=[0, 1, 4,9, 16, 25]みたいなイメージです。（実際にはyvにはノイズを載せます。）

さて、このestにたどり着くまでに、実際には私はまた間違いを犯しました。np.linalg.solveは重そうな気がして、逆行列を明示的に求め、

def est_wrong(xv, yv):
    a = []
    for x in xv:
        a.append(phi(x))
    a = np.matrix(a)
    b = np.array(yv)

    A = a.T * a

    B = a.T * np.matrix(b).T
    w = A.I * B
    return w

のようなコードを書いたのですが、これはうまくいきません。逆行列を求める時点でうまくいっていないらしく、訳のわからない結果が出ます。

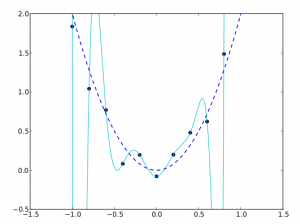
さて、話を本筋に戻しましょう。\(y = 2 x^2 \)からサンプリングしたデータにノイズを載せたものに対してestを実行した結果のスクリーンショットを以下に載せます。近似する曲線としては、\(y = w_0 + \ldots + w_{16} x^{16}\)を使いました。青い点線が理想的な曲線で、水色の曲線が多項式フィッティングの結果です。

予想通りの挙動ではあるのですが、与えられたデータ点を通ることを重視しすぎており、もとの曲線を復元することには失敗してしまっています。これは、データ点の数よりも高い自由度を曲線に与えてしまったことが原因です。自由度が高い場合、二乗誤差は0にすることができるのですが、その結果は多くの場合、人間の求めるフィッティング結果とは大きくかけ離れてしまいます。

そこで、正則化項というものを加えます。正則化はパラメーターのそれぞれの値が0から遠ざかる事にかけるペナルティで、例えばL2正則化という種類の正則化は、以下の式で書けます。

\(||\textbf{w}||_2 = \sum_i w_i^2\)

正則化項を加えると、最小化すべき目的関数は次のようになります。\(\sum_i \{y_i – f(x_i)\}^2 + ||\textbf{w}||_2\)

正則化をかけた最小二乗法はリッジ回帰と言い、以下のような関数でその推定を行うことができます。

def est_with_l2(xv, yv):
    lmd = 1.0e-4
    a = []
    for x in xv:
        a.append(phi(x))

    a = np.matrix(a)
    b = np.array(yv)

    identity = np.diag([lmd for x in range(0, a.shape[1])])

    A = (a.T * a + identity)
    B = a.T * np.matrix(b).T
    w = np.linalg.solve(A, B)
    return w

単位行列の作り方の辺りにいかにもpython初心者な感がにじみだしていますがお許しください。

estとest_with_l2を比べてみると、単位行列をlmd倍したものをAという行列（数式側のnotationだと\(\textbf{X}^T \textbf{X}\)に相当します）に足しているだけです。

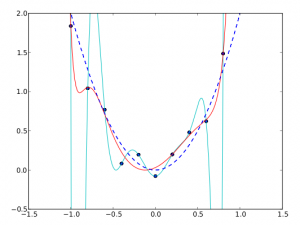
さて、正則化をかけたらいっきにぐっとよくなることを期待して実験をしたのですが、それなりに動くものの、そこまで激的な効果は得られませんでした。以下にその結果を載せます。赤の曲線が正則化項を付け加えた場合の結果です。