Blog
2022.05.30
Development of Universal Neural Network for Materials Discovery
So Takamoto
Material Science Team, Researcher/Engineering Manager

(So Takamoto, PFN Researcher) This blog post is a commentary article on the paper published on Nature Communications on May 30, 2022, titled ”Towards Universal Neural Network Potential for Material Discovery Applicable to Arbitrary Combination of 45 Elements” [1]. The original paper is open access and can be viewed at: https://www.nature.com/articles/s41467-022-30687-9
The key technology described in this paper, called PFP, is used as a core technology in Matlantis™, a general-purpose atomistic simulation software provided by Preferred Computational Chemistry, a joint venture established by Preferred Networks (PFN) and ENEOS Corporation. This research was conducted as the joint research between PFN and ENEOS Corporation.
Summary
- A fast atomistic simulation technology capable of handling unknown structures was desired for materials discovery.
- We developed a deep learning based atomistic simulation technology, PFP, by constructing a new dataset targeting a general-purpose usage and designing our own neural network architecture using PFN’s supercomputer.
- PFP was applied to a variety of real-world applications, including materials discovery, and was shown to have quantitatively good performance.
Background
Materials Discovery and Atomistic simulation
Materials development is closely related to the development of science and technology. Technological developments, such as the use of alloys and plastics, nitrogen fixation, and advances in semiconductor, etc., have often been integral to materials development. This relationship is also considered to be the same for upcoming technologies such as carbon-neutral technologies and renewable energies, and materials development continues to be a technological driver of social development.
The various materials in our world, including ourselves, are made up of a collection of atoms consisting of at most 100 different elements. The origin of the various properties of matter can often be traced back to atomic level behavior. Therefore, there have been active attempts to explain the material properties from the atomic level. In recent years, especially with the development of computers, materials development using physical simulations has been widely conducted. Because the theoretical number of possible material candidates is extremely large and it is believed that only a small fraction of them have been discovered so far by mankind, the ability to discover materials in computers has the potential to become a very attractive tool in future society.
A longstanding issue in aiming to describe the world by physical laws and simulations has been the construction of low-cost and versatile approximate models. Because of the extremely unrealistic computation time required to calculate quantum mechanics directly without approximation, which describes phenomena at the atomic level, simulation techniques have been proposed that introduce various approximations, collectively known as quantum chemical calculations. Density functional theory (DFT) is one of the quantum chemical calculation methods that have succeeded in achieving both cost and accuracy. However, real-world phenomena of interest often require times of at least the order of nanoseconds and scales of nanometers or larger, and simulations require as many as 1 million steps or 1,000 atoms in a single calculation. In these cases, there is still a gap of many orders of magnitude between the scale that can be calculated and the scale that one wishes to reproduce.
Neural Network Potential
For this reason, computational models have been considered that bypass quantum chemical calculations and directly estimate the results. In particular, computational models that estimate energy surfaces with the aim of reproducing the dynamics of atomic structures are called potentials (interatomic potentials, force fields), and many empirical potentials applicable to individual materials have been considered. In recent years, with the development of deep learning, neural network potentials (NNP), in which potentials are modeled by neural networks, have attracted attention and are being actively researched and developed as both a field of deep learning and a field of materials informatics.
NNP has a number of unique features compared to other NN application areas. For example, the input data is a graph of indefinite size embedded in a 3-dimensional space, and the 3-dimensional positional relationships between neighboring nodes are of interest. The target value is energy and NNP can be regarded as a scalar value regression problem. However, the derivative of the output is also used during inference (the derivative of energy with respect to coordinates, corresponding to the force acting on the atoms). In addition, the inference model is usually used directly by a physical simulator, not by a human, and the simulator frequently performs input modifications such as changing atomic positions slightly and uses the inference model over and over again. Therefore, it is desirable for the simulator to satisfy various physical constraints that are prerequisites for the simulator to operate, e.g., the energy is invariant with operations such as rotation and translation or it is not discrete. A deep learning architecture for NNP has been proposed that satisfies these conditions, and significant improvements in accuracy have been reported.
Materials simulation using NNPs has recently moved beyond the basic research stage and is attracting attention in a wide range of areas for applications. In 2020, Facebook AI Research and Carnegie Mellon University have launched the Open Catalyst Project which aims to use AI to model and discover new catalysts for use in renewable energy storage. [2] The topic of the Gordon Bell Prize in 2020, commonly referred to as the Nobel Prize of Supercomputing, was also related to the massively parallel computation of NNP. [3]
Challenge
However, even with these innovations, a major challenge still remains in materials discovery. It is the generalizability in dealing with unknown materials.
In the past, potentials have usually been developed as reproducing a specific material or a specific phenomenon. This was because it was believed that potentials had to be developed targeting a specific atomic structure to ensure sufficient accuracy.
This has been true for NNP as well. All previously proposed datasets were generated based on known structures. Relatedly, as new datasets have emerged, it has been an iterative process of coming up with effective NNP architectures for them. To compare this to self-driving cars, one can think of the analogy of having a dataset for each specific city or street and developing a self-driving car AI for that city or street. This was a reasonable way to think about creating an accurate inference model with a limited dataset.
However, the task of materials discovery requires potentials to perform well with unknown or hypothetical materials. For example, when considering a new hypothetical material, one must consider whether such a material can exist in reality and whether it will react chemically as expected. In other words, being able to handle known materials is not sufficient. It is said that there are 10 to the 60th power of candidates in the world of materials even if limiting to the form of functional molecules, and the number of combinations far exceeds that when it comes to complex structures to reproduce phenomena. Therefore, it is unrealistic to create a dataset that covers all structures. In the previous example of self-driving cars, this can be compared to the desire to be able to drive in an unfamiliar place because the city is spread out without limit.
Then, is it not possible to create a universal potential? Again considering the problem to be solved, in the world of atoms, the characters are the elements, of which there are a finite number of varieties. Moreover, their interactions are not unpredictable, but rather well described by a single equation, the Schrödinger equation. In addition, looking at recent NN research, we can find several positive examples. For example, in the field of natural language processing, general-purpose language models have emerged and have attracted a great deal of attention due to their high performance. Thus, in some areas, the acquisition of some kind of universality is actually coming to fruition.
This led us to believe that if a suitable dataset, NNP architecture, and sufficient computational resources are available, it would not necessarily be impossible to obtain a “universal NNP” with an internal representation of general atomic interactions. So we set our sights on this ambitious task, identified the problems to be solved, and proceeded to develop the elemental technologies.
Methods
Both the dataset and the architecture are important for NN development and we have been developing both of them. We called PFP for the obtained NNP.
The dataset is constructed to include as many different patterns as possible by actively collecting unstable structures. The dataset is not limited to a database of known materials, but rather is actively constructed to include hypothetical structures, for example, by setting all combinations of elements to a certain atomic structure. This is a very different policy from conventional datasets that collect known stable atomic structures. Specifically, we try to include structures in which elements are irregularly substituted in various crystalline and molecular structures, disordered structures in which various different elements are present simultaneously, and structures in which temperature and density are varied. The number of element types covered is 45 at the time of paper submission.
Building such a novel data set from scratch required considerable computational resources. The target values are obtained by DFT calculations. As mentioned above, DFT calculations are computationally expensive. However, in addition to keeping the computation target to an appropriate size, we created a dataset of a certain size by using more than 164 years worth of GPUs in the PFN clusters (MN-1 and MN-2) in total.
In the actual development process, through the development of the NNP architecture and its application to actual simulations, we are repeatedly providing feedback on the dataset construction procedure to ensure that it is as universal as possible. This makes it an ambitious effort in which the more advanced the dataset becomes as the research progresses, the more challenging the development becomes. Shinagawa, a PFN engineer, took the lead in this effort. (Note that we have continued to build the dataset since the paper submission, and at this point, the dataset has exceeded 1000 years worth of GPUs.)
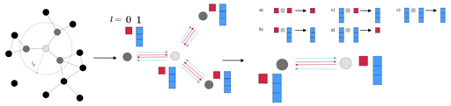
The NNP architecture must also be designed to handle such a disordered structure without failure. The architecture is based on TeaNet [4], an original graph neural network (GNN) devised by PFN researcher Takamoto, with additional improvements. This architecture combines GNN with physical models that have been incorporated into empirical potentials, and is a model that flows second-order tensor quantities in a graph. It allows the model to have the physical requirement that the phenomena remain the same for rigid body rotation, rigid body movement, etc., while capturing local positional information.
Dataset and architecture development are truly two sides of deep learning, and the development of both techniques increased what we could do. During the course of development, it became possible to use the NNP obtained through training to perform atomistic simulations and obtain additional datasets from them.
A subset of the dataset created in this way is available as the High-temperature multi-element dataset (HME21) (https://doi.org/10.6084/m9.figshare.19658538). As mentioned earlier, this study constructed a dataset with a very messy atomic arrangement for universality, which is considered more challenging than existing datasets for NNP.
As a stand-alone performance evaluation of the NNP architecture, we also include benchmark results of the NNP architecture using HME21 dataset in the paper. The benchmarks are based on the original TeaNet. It can be seen that it achieves high performance compared to other NNP architectures.
The publish of HME21 dataset has three main purposes: First, to provide additional information on how to create a dataset for universal NNPs as described in the paper; second, to provide a benchmark dataset to demonstrate the performance of the PFP architecture; and third, to be used as a dataset in future NNP development. We hope that through the HME21 dataset and other products of this research, the academic area related to universal NNPs will be further developed.
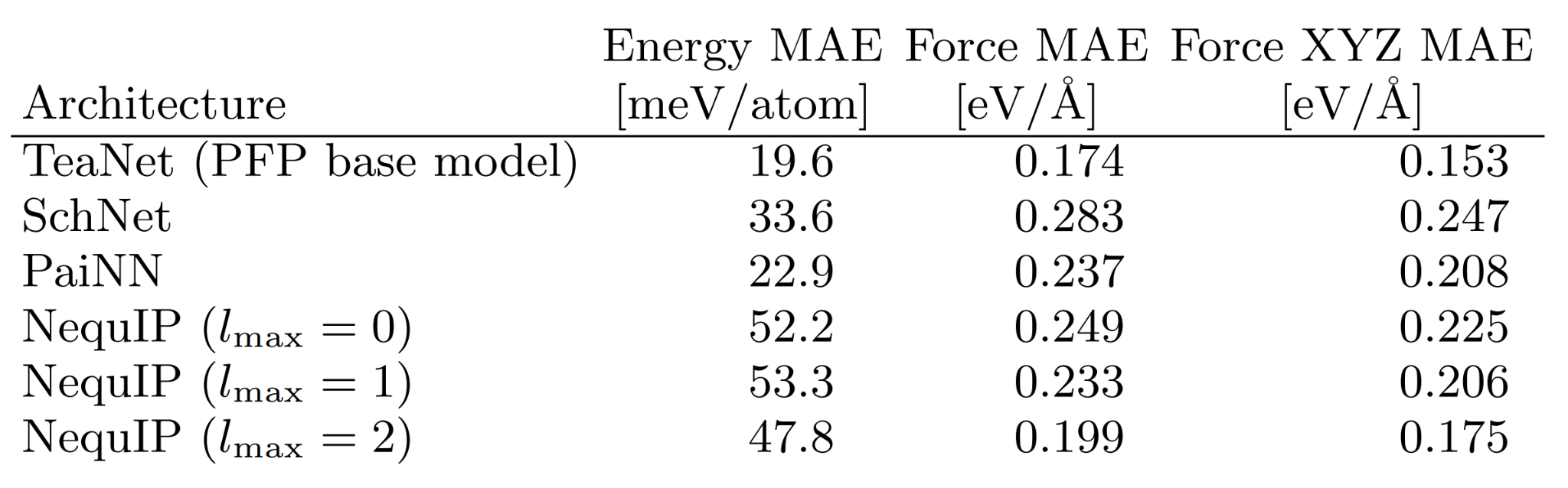
Benchmark performance of NNP for the force and energy prediction for the HME21 dataset. Excerpt from [1].
Results: Material Simulations using PFP
We applied PFP to real examples of material simulation. As noted in the background, since our goal is materials discovery, it is not enough to simply look at the fit to the dataset; we need to investigate whether the performance is good for real-world problems.
In this paper, we used four atomistic simulation examples that are very different from each other in terms of materials and target phenomena: i) lithium diffusion in lithium-ion battery material, ii) molecular adsorption in metal-organic frameworks, iii) Cu-Au alloy order-disorder transition, and iv) materials discovery for a Fischer-Tropsch catalyst. As you can see from the author contribution section in the paper, many members of the project are involved in material simulations using PFP. Although not included in the paper, many other applications have been attempted in addition to these four examples. Some examples are also available on the Matlantis web page for those interested: https://matlantis.com/cases
In the following, the four examples are presented individually. However, since an in-depth explanation of each example would be quite lengthy, we will leave a detailed discussion of the calculation methods and results to the paper. We would like to give a brief introduction to the materials used in each example and the technical features of the simulations.
Lithium Diffusion in Lithium-ion Battery Material
The importance of lithium-ion batteries is increasing day by day, especially in electric vehicles and portable devices. One of the important properties of lithium-ion batteries is the charge-discharge rate. The ease of diffusion of lithium atoms in a material is related to this, and a property called activation energy is noteworthy.
The target in this study is the task of reproducing the behavior of interstitial atoms in bulk crystals. In particular, since the diffusion phenomenon is governed by the highest energy point in the middle of the path (saddle point), we must be able to correctly reproduce such an energetically unstable structure. The nudged elastic band (NEB) method and auxiliary molecular dynamics (MD) calculations are used.
In this application, activation energies are investigated for three different diffusion paths. All of them perform well and reproduce the results of the DFT calculations of previous studies.
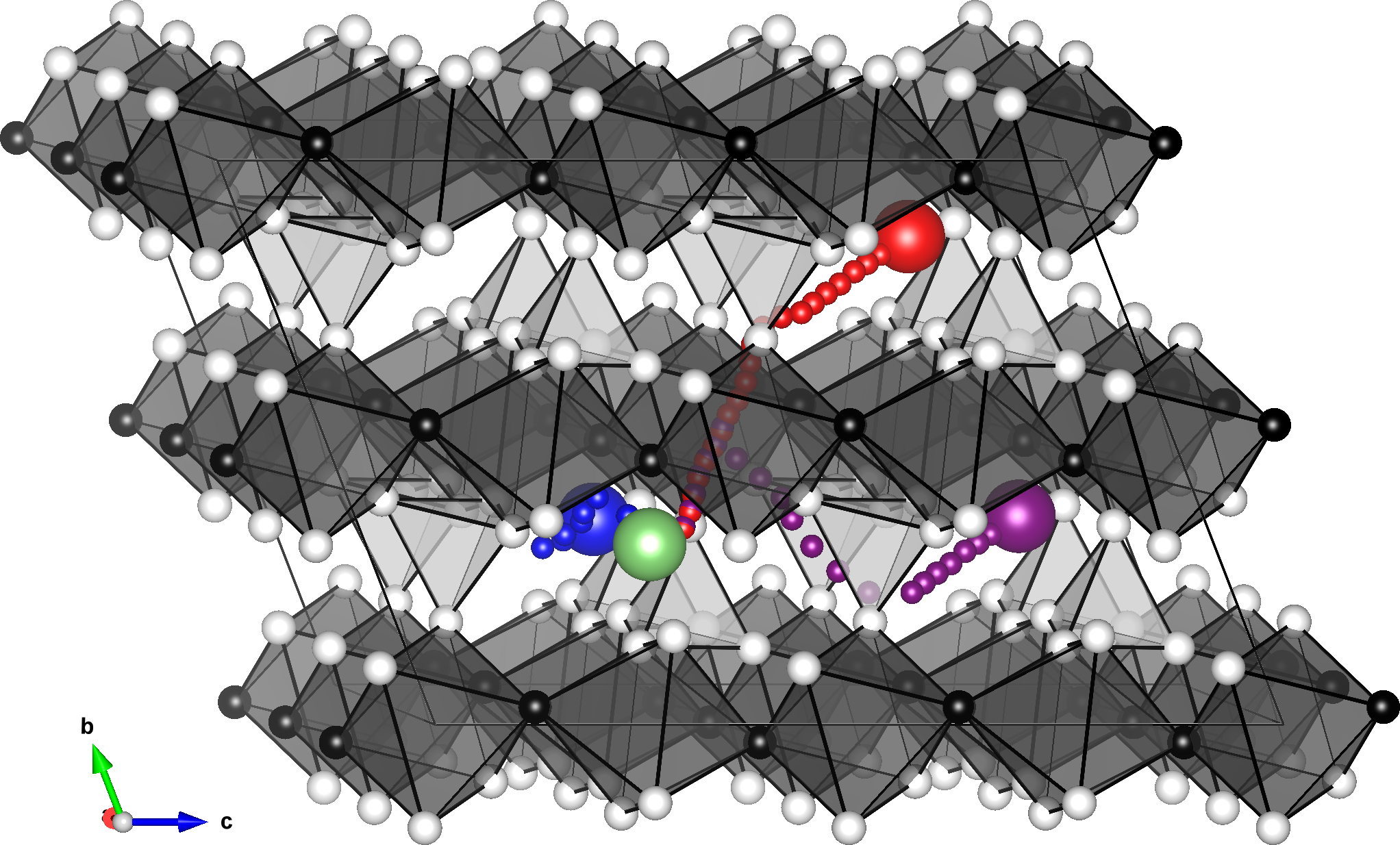
Lithium diffusion paths. Excerpt from [1].
Molecular Adsorption in Metal-organic Frameworks
Metal-organic frameworks (MOFs) are a type of nanoporous materials with extremely high surface area. The pore structure can be artificially controlled by using various molecules. For some metal atoms, active unsaturated sites can be the locations for the adsorption of various small molecules and may act as metal centers for catalytic reactions.
The targets in this study are the reproduction of MOF structures and adsorption energies of water molecules. Because MOFs are complex chemical structures containing both organic and inorganic parts, it is necessary to reproduce structures containing diverse elements with high accuracy, which makes it difficult to utilize conventional potentials. We also investigate the adsorption energy of water molecules on the adsorption sites of metals. The calculations also incorporate an additional van der Waals interaction correction, the D3 correction, into the comparison of the results of the calculations.
In this application, eight different MOF structures and five different adsorption energies are evaluated. All of them have been estimated with average errors within a few percent.
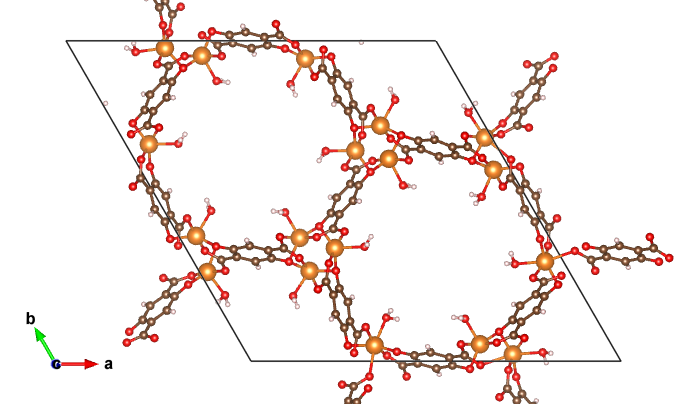
MOF structure illustration. Excerpt from [1].
Cu-Au Alloy Order-disorder Transition
Cu-Au alloys are materials that have been studied as catalysts for CO and alcohol oxidation. Cu-Au alloys are known to be fully miscible over a wide composition range and exhibit an order-disorder transition. Local microscopic structures and atomic arrangements are essential for the performance of the catalyst and is an important factor in elucidating the phenomena.
The target in this study is to reproduce the phase transition between ordered and disordered structures in alloys. In addition to the need to reproduce metallic bonding to reproduce the alloy itself, it is necessary to be able to accurately reproduce the change in energy due to the disorder in the configuration. The Metropolis Monte Carlo method is used in this study.
In this application, the temperature of the phase transition is investigated for three compositions, Cu3Au, CuAu, and CuAu3, and the same behavior is calculated as in the experiment, with the temperature of the phase transition being highest for CuAu.
Materials Discovery for a Fischer-Tropsch Catalyst
Fischer-Tropsch (FT) reaction is a catalytic synthesis of hydrocarbons from hydrogen and carbon monoxide. This reaction is gaining attention as a technology to create an alternative to petroleum from sustainable energy sources. In this study, we also conducted a practical case of materials discovery to find promising additive elements.
The targets in this study are the methanation reaction on the cobalt surface and the dissociation process of carbon monoxide. This is a phenomenon involving many elements, such as metal surfaces, organic materials, chemical reaction processes, and the effects of surface adsorption. In this study, 20 elementary reactions are compared with previous DFT studies. In addition, we have explored catalytic structures by substituting elements and benchmarked whether PFP can be used for materials discovery.
In this application, the activation energies were reproduced with good accuracy, with the mean absolute error of less than 0.1 eV. In addition, it was suggested that the addition of vanadium is promising, and a search of the literature revealed that there are in fact experimental reports showing that the addition of vanadium has positive effects.
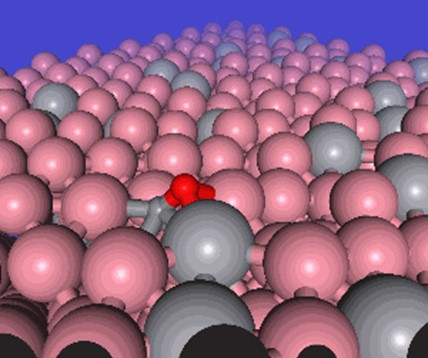
CO adsorbed configuration of a Co surface with V promoters. Excerpt from [1].
Discussions, Other Topics
- In all of the above examples, not only did the simulations work, but they produced results that can be quantitatively discussed. It is particularly impressive that we were able to reproduce them even though we did not explicitly include these materials in the dataset construction phase, and that all four of these examples could be reproduced using a single model.
- The examples presented here are examples where DFT calculations or other measurements have been performed in previous studies for quantitative comparison of the results. It is noteworthy that the PFP-based calculations are fast, whereas the previous studies required a large amount of computational resources to simulate the systems. The ability to perform large-scale calculations is expected to increase the degree of freedom in simulations and enable a wide range of materials discovery. It will also allow researchers to rapidly repeat hypothesis testing through interactive research.
- As an example of a comparison of computation time, a system of 3000 atoms of platinum was used as an example: a single structure required an estimated 2 months to compute with DFT calculation, whereas with PFP, the computation was completed in 0.3 seconds. This is equivalent to a speedup of the order of 10 million times by PFP.
- Although not covered in this blog post, other topics related to NN training are also included in the paper. For example, NNPs are trained on multiple datasets that are not exactly consistent with each other, depending on how they are approximated. Here, we see interesting behavior in terms of generalization performance, such as elements that are only included in dataset A working in general in the inference to dataset B.
Future
- We develop Matlantis, a software-as-a-service for materials discovery that uses PFP as the core technology. Matlantis provides an environment where users can perform atomistic simulations using PFP.
- After the paper submission we continued our research and development efforts. Since the model discussed in the paper, PFP has undergone two major updates in Matlantis, and the size of the dataset based on DFT calculations now exceeds 22 million structures with over 1,000 years worth of GPU use, continuing to further improve accuracy and expand coverage. Increasing computational speed and scale for broader materials discovery are also important issues.
- Efforts to discover specific materials using PFP are also underway. We are also continuing our research into the integration of computational materials science and deep learning outside of NNP. There are important engineering issues on both the small and large side of the scale compared to molecular dynamics, and we are investigating the application of machine learning techniques either separately from NNP or in combination with NNP. If you are interested in any of these activities, please contact us.
- On a related note, we are also developing techniques on the scale of molecular dynamics. The availability of universal NNP is like having a map on which to explore the ocean of materials. While this is certainly a useful technology on its own, we believe that the horizon of materials exploration will be further expanded by using this map to refine the technology for a bird’s-eye view of the vast world of materials. The integration of machine learning and physical simulation seems likely to continue.
- Last but not least, PFN is looking for new members to work with us in the field of materials science; there are many ways to get involved in various aspects from Matlantis service development to elemental technology development and materials discovery, so please contact us if you are interested.
Case Study
- Matlantis Case Study: High-speed atomistic simulator revolutionizes catalyst development
References
[1] So Takamoto, Chikashi Shinagawa, Daisuke Motoki, Kosuke Nakago, Wenwen Li, Iori Kurata, Taku Watanabe, Yoshihiro Yayama, Hiroki Iriguchi, Yusuke Asano, Tasuku Onodera, Takafumi Ishii, Takao Kudo, Hideki Ono, Ryohto Sawada, Ryuichiro Ishitani, Marc Ong, Taiki Yamaguchi, Toshiki Kataoka, Akihide Hayashi, Nontawat Charoenphakdee, and Takeshi Ibuka “Towards universal neural network potential for material discovery applicable to arbitrary combination of 45 elements” Nature Communications, 13, 2991 (2022). https://doi.org/10.1038/s41467-022-30687-9 CC-BY 4.0 (http://creativecommons.org/licenses/by/4.0/)
[2] Open Catalyst Project. https://opencatalystproject.org/
[3] https://www.acm.org/media-center/2020/november/gordon-bell-prize-2020
[4] So Takamoto, Satoshi Izumi, Ju Li “TeaNet: Universal neural network interatomic potential inspired by iterative electronic relaxations” Computational Materials Science, 207, 111280, DOI: 10.1016/j.commatsci.2022.111280 (2022).