Blog
This is a guest blog from a part time engineer, Masaki Kozuki (@crcrpar).
This post requires some familiarity with Optuna and targets those who are rather interested in software for Machine Learning and Deep Learning than ML and DL technologies and/or algorithms themselves. Also, I hope some of you feel like giving Optuna a try, or contributing to Optuna after you read this.
If you’re new to Optuna, here’s the quickstart on colab, v1 release announce post! 🙂
TL; DR
- Sampler and Pruner of Optuna are loosely connected for modularity.
- Optuna has experimentally supported Hyperband [4] now from v1.1.0, one of the most popular and competitive hyperparameter optimization (HPO) algorithms.
- Challenges in implementing Hyperband in Optuna is discussed in this post.
- We resolved the challenges in a simple and beautiful manner.
- We can use competitive hyperparameter optimization of Hyperband with ease. Feel free to try it now! Benchmark results are shown later.
In the first section, I briefly introduce the structure/modules of Optuna. Then I’ll illustrate how pruning algorithms work with a naive algorithm. After that, Successive Halving, a popular HPO algorithm is introduced and its weak points are discussed. Last, Hyperband is introduced and how we implemented is described.
Under the Hood of Optuna
If you are already familiar with Optuna, feel free to move on to the next section.
Optuna finds the best hyperparameter configuration from a number of possible hyperparameters. Under the hood, there are five major components in Optuna:
A Study object is responsible for finding the set of hyperparameters that achieves the best value of the user-defined objective function. One set of hyperparameters and values of the objective function obtained by this set are monitored by one Trial. Trial reports those values and its ID (Trial.number) to Storage of Study. Sampler is in charge of the sampling processes of hyperparameters. Pruner stops unpromising Trials by comparing its intermediate values with those of previous Trials. Note that Pruner is not always enabled. It works only when you report the intermediate values through Trial.report within your objective function.
How Pruning Algorithms Work
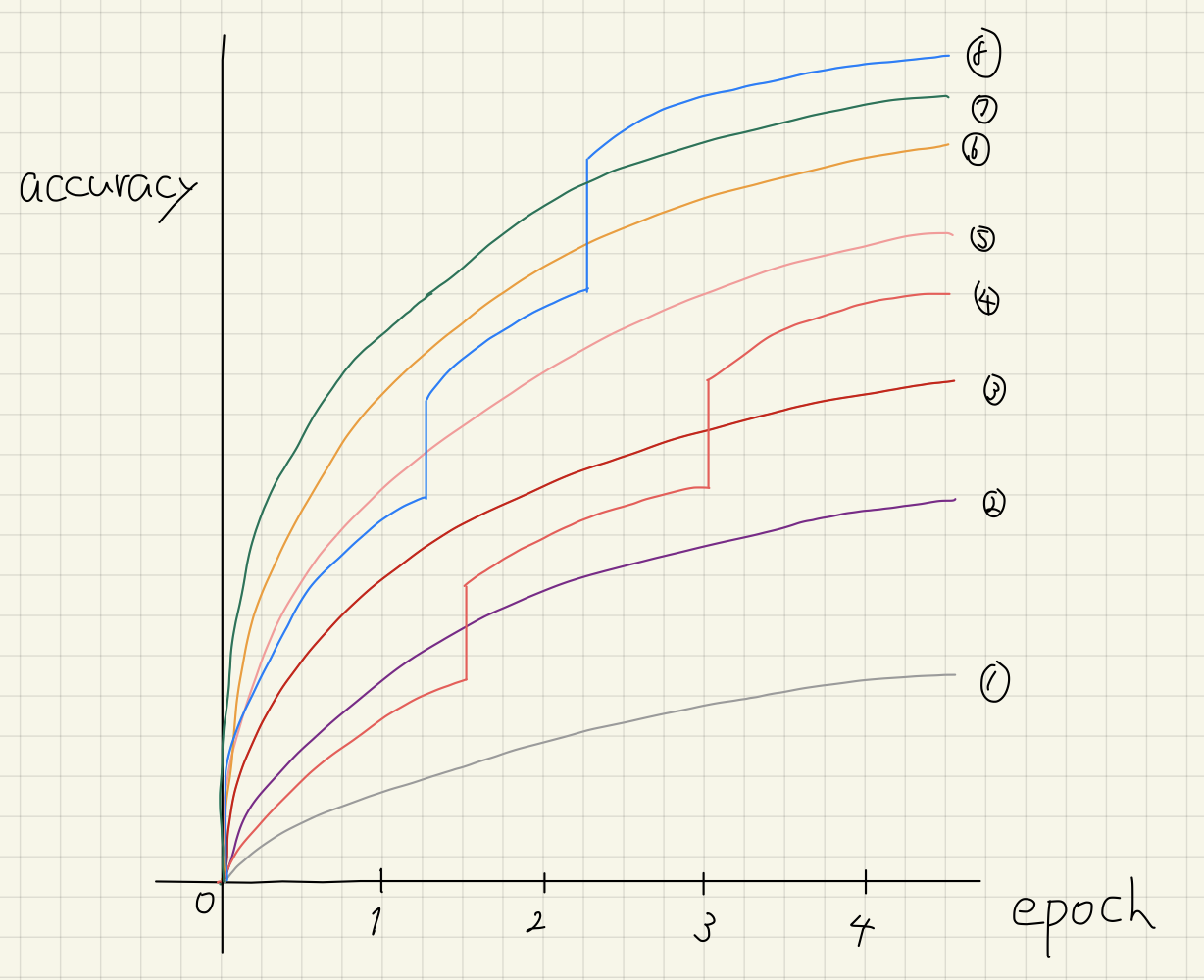
Before diving into Hyperband, let us go through an example of a basic pruning algorithm to show how it works and the best hyperparameter configuration might be overlooked. Every epoch, we cut off the worst half of the running configurations. Assume there are eight hyperparameter configurations and learning curves of their complete training are as follows. Note that these curves are NOT available before hyperparameter optimization.
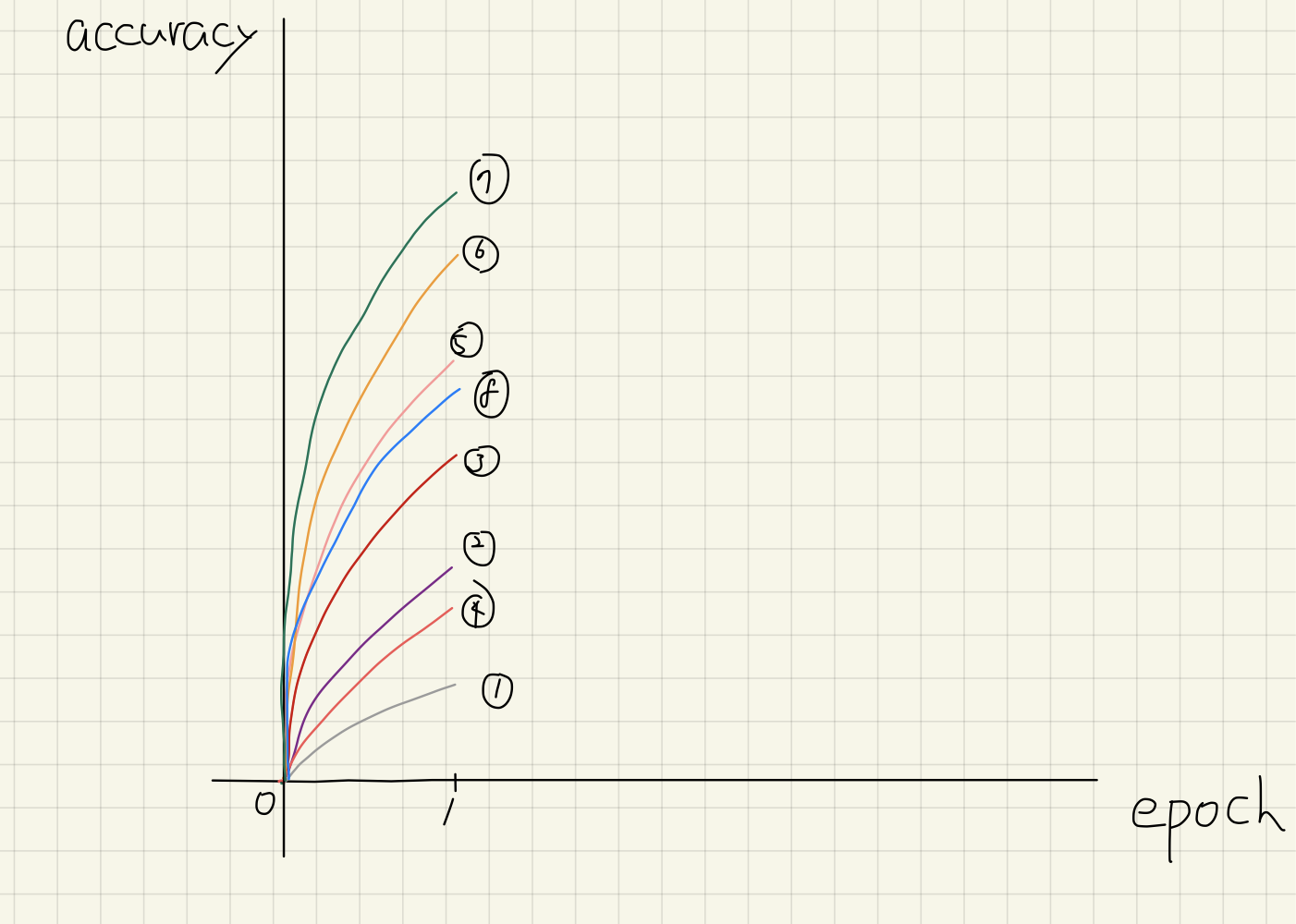
First, we run 8 configurations for one epoch to collect the validation accuracy of them.
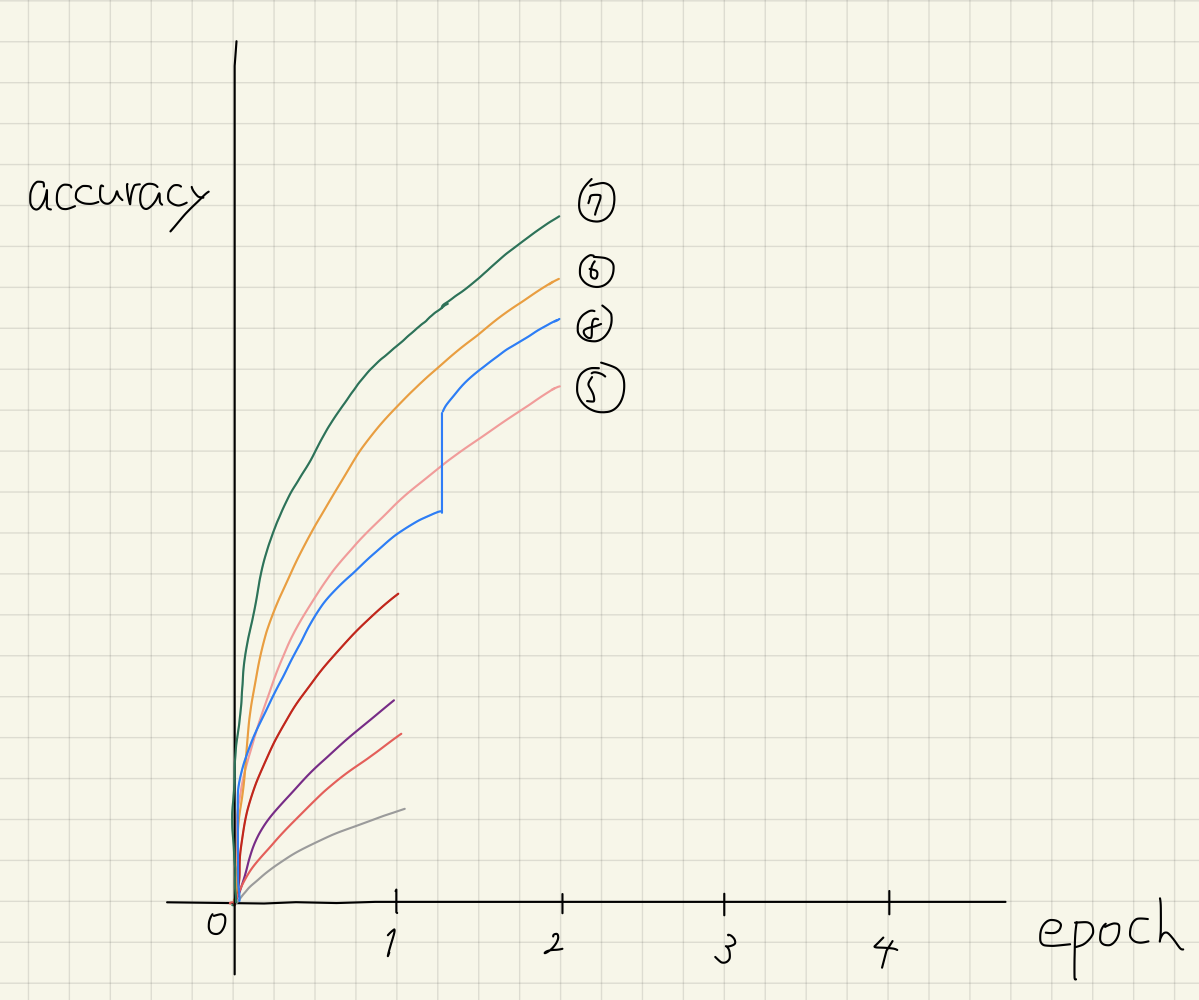
Here, the bottom four configurations, i.e., 1, 4, 2, and 3 are stopped. We repeat this procedure until there is only one configuration. So, we run the remaining four configurations for another epoch.
As of epoch 2, 5 and 8 are pruned. The algorithm fails to detect that 8 is the ultimate best configuration at this moment.
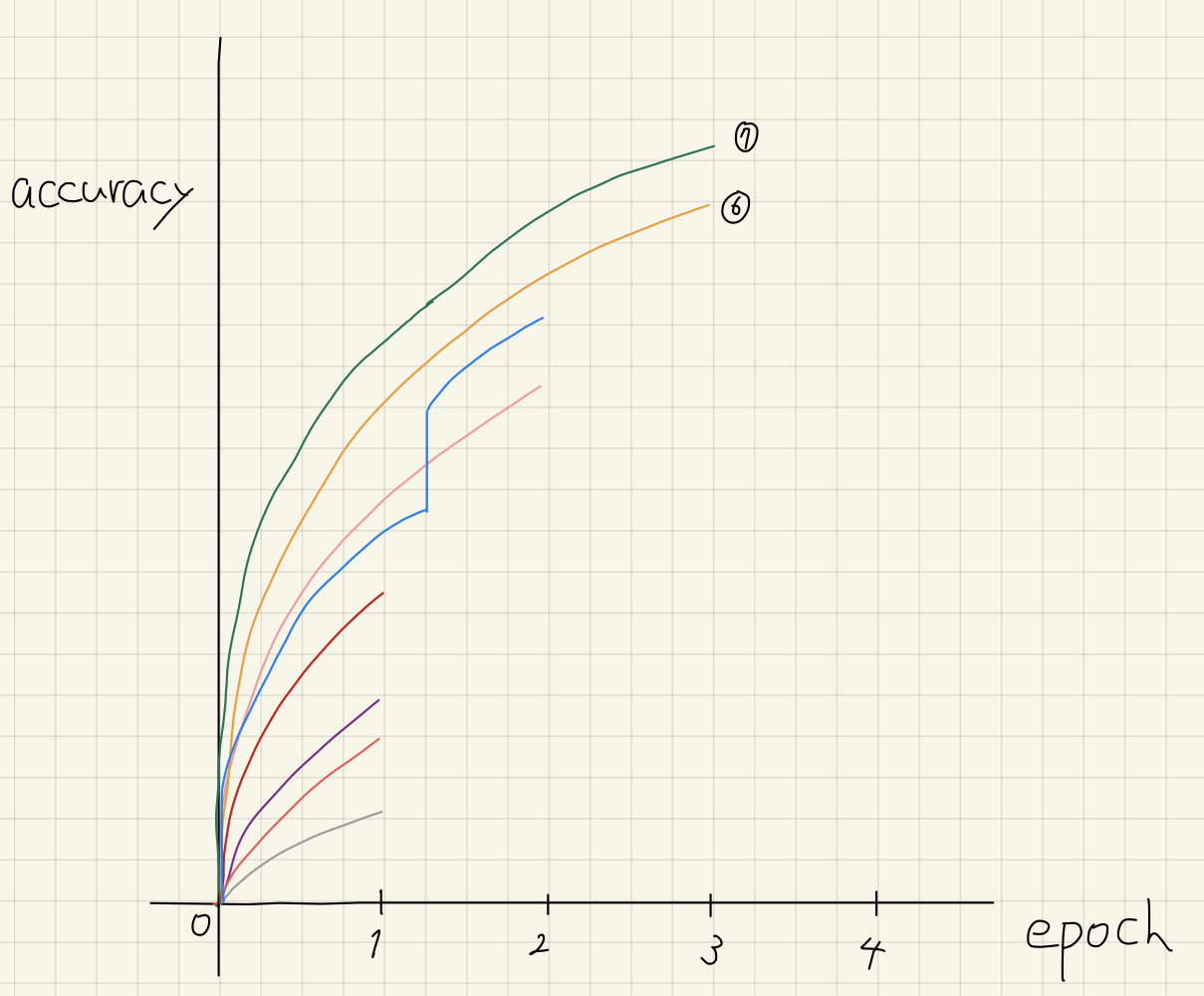
After 3 epochs of training, configuration 7 is better than 6. 7 will be trained fully.
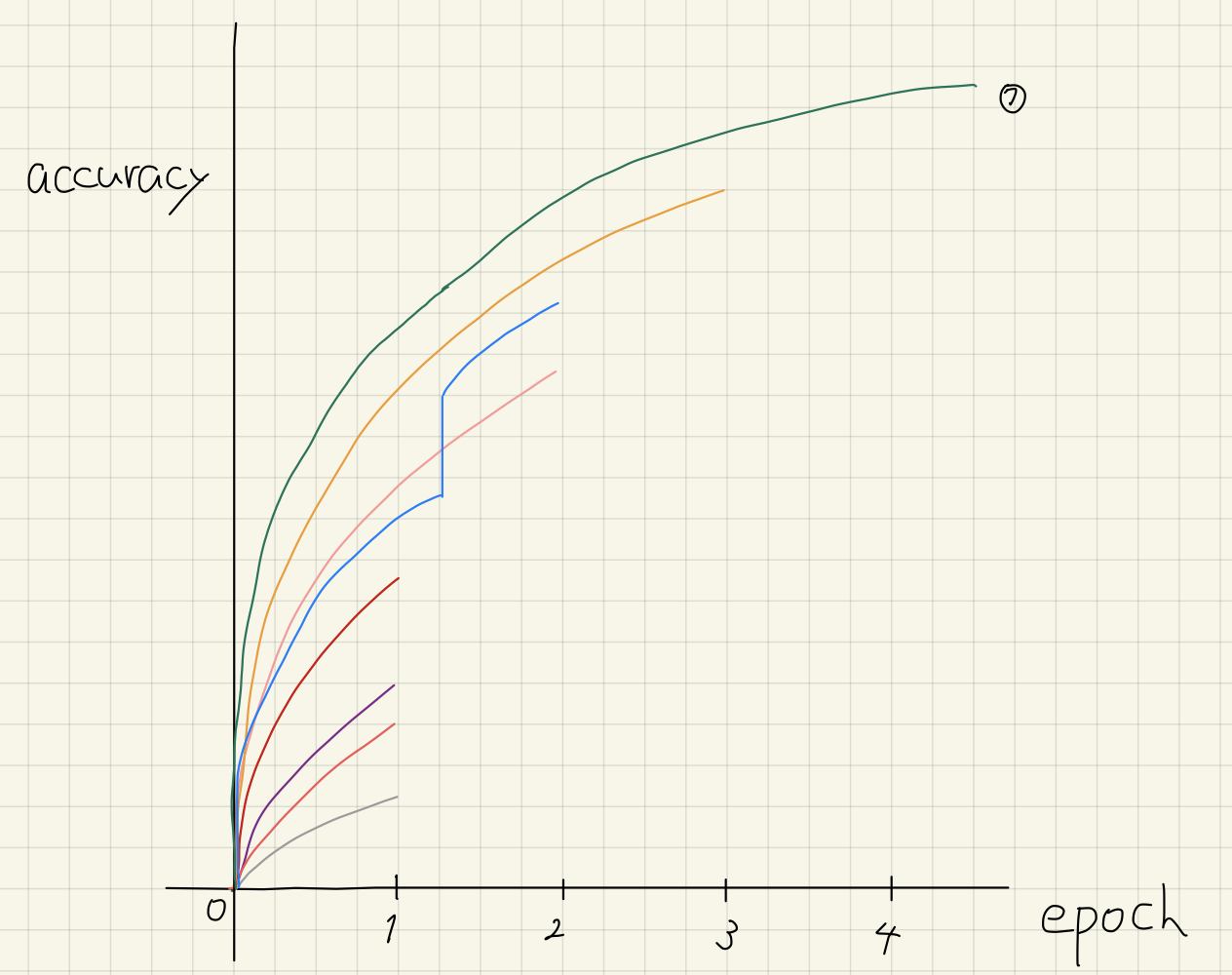
As you might notice, pruning algorithms might stop the best configuration prematurely, however, there is no way to prevent this as we cannot predict learning curves 100% accurately with any algorithms.
Optuna’s Pruning Algorithms So Far
Optuna has provided basically two pruning algorithms: median stopping rule [1] and (asynchronous) Successive Halving (SHA) [2][3] named MedianPruner and SuccessiveHalvingPruner, respectively. Median stopping rule “prunes if the trial’s best intermediate result is worse than median of intermediate results of previous trials at the same step” (quote from Optuna documentation). SHA introduces the concept of budget (hereafter, denote it as B) that is equivalent to the computational resources of HPO experiment. The design principle is that allocating more resources, e.g., epochs, to promising trials by reducing the number of trials to half, i.e., stopping unpromising ones. In this situation, the intervals grow exponentially by the user-defined ratio (e.g. 3). However, as its focus is on faster configuration evaluation rather than hyperparameter configuration selection of Bayesian Optimization, Successive Halving has a hyperparameter for itself related to the number of trials to examine (hereafter, denote it as n). This means that SHA has a tradeoff between n and B. When it requires more resources to differentiate better configurations from worse ones, i.e. learning curves can change drastically in their training, it’d be better to set n small to reduce the wrong judgment. Contrary, if learning curves change monotonically, i.e., their order does not change during the training, we have to set n larger to expand the probability of finding better hyperparameters.
For further details, please refer to the original papers and the post by the authors.
What is Hyperband
As mentioned briefly, Successive Halving has hyperparameters and they are in the relationship of trade-off. This trade-off, called “n versus B/n” in the Hyperband paper, affects the final result of HPO. Of course, all the trials can be correctly sorted and selected if the final results are available. But, pruning tries to stop unpromising trials as quickly as possible and how learning curves are shaped is totally different. Also, to judge which trial is better than the other with enough confidence, there should be enough gap between the two trials. If there is some prior knowledge about the tendency of learning curves are available a priori, we can choose appropriate n. However, what makes things complex and challenging is that the characteristic of learning curves is up to the task.
To address this trade-off, Hyperband runs multiple Successive Halving instances with different n values and each instance is responsible for a portion/subset of the trials, called brackets.
Implementing Hyperband in Optuna
In this section, first I’ll show you the most naive implementation and discuss weak points of it. Then, necessary characteristics of Hyperband implementation, difficulties in realizing those features, and how we resolved them are explained.
The Naive Implementation and What it sacrifices
The simplest implementation of Hyperband with Optuna is that using multiple Studys as follows.
def main():
best_trials = []
for bracket_config in all_bracket_configs:
sampler = ...
pruner = SuccessiveHalvingPruner(**bracket_config)
study = optuna.create_study(sampler=sampler, pruner=pruner)
study.optimize(objective, ...)
best_trials.append(study.best_trial)
best_trial = min(best_trials, key=lambda trial: trial.value)
...
This is solid as it’ll be easier to implement the algorithm described in the paper truly but only if you don’t care how to resume this optimization workflow (optuna.load_study), how to manage storage, and/or how to execute this implementation in a distributed environment correctly. Since distributed execution is one major feature of Optuna, it is not desirable to give up it partially just by adding a new feature however it’s impactful.
Challenges to Keep the Current Design and How We Resolved
So we decided to implement Hyperband in the same manner as the other pruners. In this way, there were three challenges:
- how to choose a bracket for a new trial
- how to compute budgets of brackets
- how to collect trials of one single bracket in pruning/sampling phases
In each section, the design decisions we made follow the description of challenges.
Challenge 1 & 2: Design of Hyperband
By definition, budget is a thing related to time, not the number of trials. So, for each bracket to consume approximately the same budget, it’s necessary to give a reasonable number of trials to brackets. Also, as Optuna allows users to run study.optimize infinitely long and stop by ctrl+c, both n_trials and timeout can be None, leading to null budget information. Thus, we decided to introduce randomness in bracket selection and bracket budget computation algorithms. This is because no algorithm can satisfy all the requirements of Hyperband and the constraints of Optuna. This design choice made the implementation a bit different from the algorithm described in the paper, however, the performance is solid in the benchmark. Also, budget computation is a bit modified but the trends of budget values follow the paper. It’s worth mention that in spite of this naive allocation, it defeats the other pruning algorithms in benchmarks executed with sile/kurobako.
Challenge 3: How to Collect Appropriate Trials
As to the implementation of trial collection in pruning/sampling, the most arguable thing. Optuna has kept pruning module and sampling module loosely coupled and this has contributed to the modularity of Optuna (This means that Study module is responsible for a bunch of tasks). So, without any modification, brackets and samplers will take into consideration the history of all the trials including ones that are monitored by the other brackets. Therefore, we needed to implement some filtering logic while keeping samplers and pruners loosely-connected as possible. We had two ideas of how to resolve.
One is adding bracket index to trials.use_attr and setting the list of trials of the same bracket as its attribute for samplers to get access to the list of trials. The required changes can be found in optuna/optuna#785. As you can see, the number of changed files is 22. This is not reasonable from the perspective of maintainability. Also, most of the changes are really ad-hoc while they are required only by HyperbandPruner.
The other is wrap a study object, especially get_trials that filters out trials based on the current trial’s bracket index as done in optuna/optuna#809. This can be implemented in a way that we can encapsulate the required ad-hoc changes inside hyperband implementations, i.e. HyperbandPruner class. How? We have implemented a wrapper class of Study whose get_trials method effectively filters out irrelevant trials before returning the list of trials. This design made it simple to make TPESampler compatible with Hyperband. Since TPESampler uses the history of HPO, it has to track which bracket monitors which configurations. This seems to require a bunch of changes, but as you can see in https://github.com/optuna/optuna/pull/828, the changes are compact.
Benchmark Results
Takeaway: the current implementation works well and easy to use.
The task is chosen from HPOBench [5].
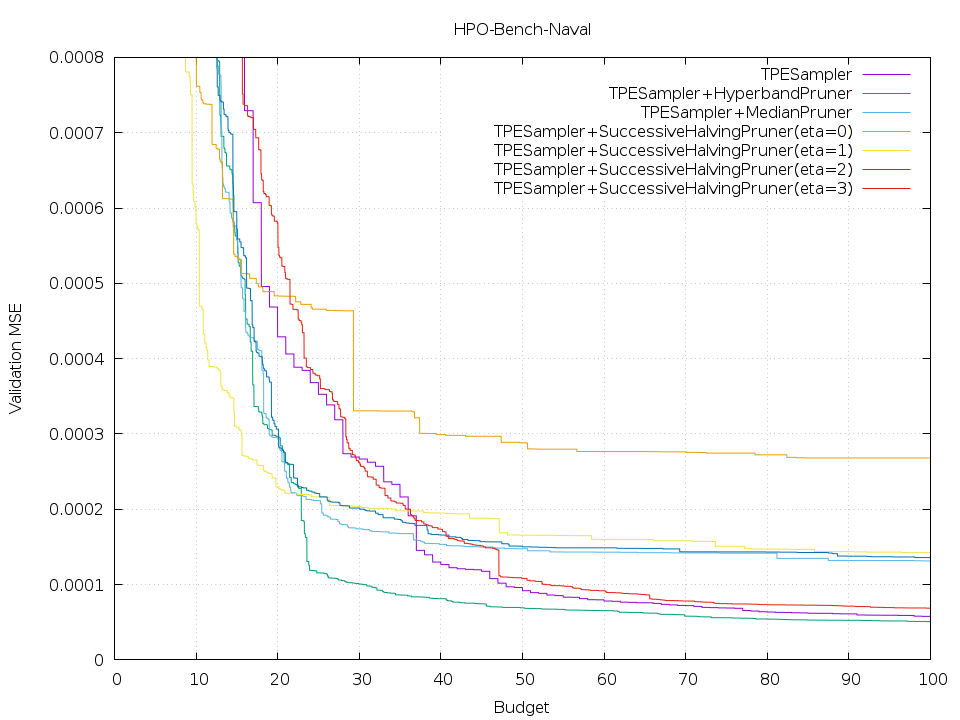
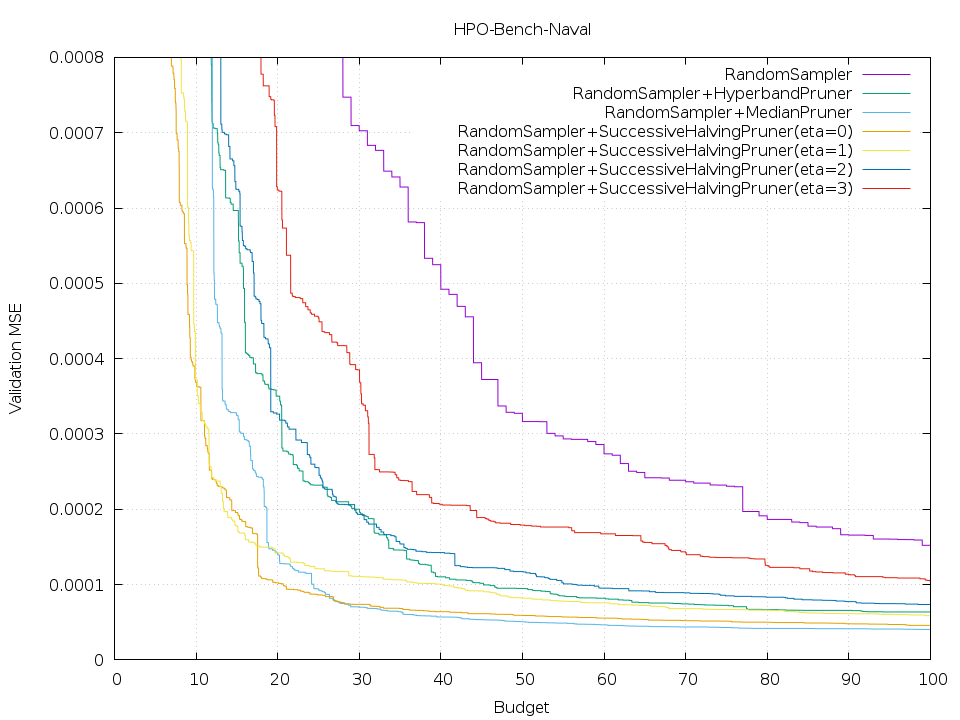
First of all, to show the benefit of Hyperband, we ran the experiment of TPESampler and different pruners. In the below figure, deep green represents the HyperbandPruner and it achieves the best performance. Intuitively, Hyperband mitigates the burden of finding the best eta value of SuccessiveHalving. Naturally, some Successive Halving instances would beat Hyperband if they use good hyperparameters. Though, it’s not true in this benchmark. We attribute this to the nature of TPESampler: it sometimes gets stuck at saddle points while HyperbandPruner virtually four TPESamplers leading to the avoidance of those local optima. It might be worth mentioning that the task is different from that of the Hyperband paper.
RandomSampler
As mentioned beforehand, SuccessiveHalvingPruners with different eta, a parameter that affects n, values show different characteristics. More specifically, the case of eta=0 is terrible while the others show achieve better and similar scores. This is “n versus B/n tradeoff.” Also, you can see that Hyperband is not the best but it looks competitive considering that we don’t need to run different Successive Halving experiments.
Conclusion
In this post, I briefed Optuna and how I implemented Hyperband. The current implementation works really well including that sometimes well configured Successive Halving is better, however, it’s experimental and there’s room to improve how to select a bracket for a Trial and how to compute budgets for SuccessiveHalvingPruners run by HyperbandPruner. Optuna team, really welcome any comments, feedback, and thoughts! Feel free to comment, join Gitter, and enjoy Optuna!
Cited Works
[1] Google Vizier: A Service for Black-Box Optimization, https://research.google.com/pubs/archive/46180.pdf
[2] [1502.07943] Non-stochastic Best Arm Identification and Hyperparameter Optimization
[3] [1810.05934] Massively Parallel Hyperparameter Tuning
[4] Hyperband: A Novel Bandit-Based Approach to Hyperparameter Optimization
[5] [1905.04970] Tabular Benchmarks for Joint Architecture and Hyperparameter Optimization
Tag







