MN-Core向けのBLASの実装

本記事は、2023年度PFN夏季インターンシップで勤務された野崎愛さんによる寄稿です。

はじめに

こんにちは。2023年度夏季インターンシップに参加させていただきました野崎愛です。
今回のインターンではMN-Core向けのBLASの実装に取り組みました。

背景: MN-Coreの概要とアーキテクチャ上の特徴

深層学習を軸とした研究開発には大きな計算資源が必要です。
PFNでは深層学習ワークロードに特化したアクセラレータであるMN-Core(https://www.preferred.jp/ja/projects/mn-core/)を神戸大学と共同開発しています。

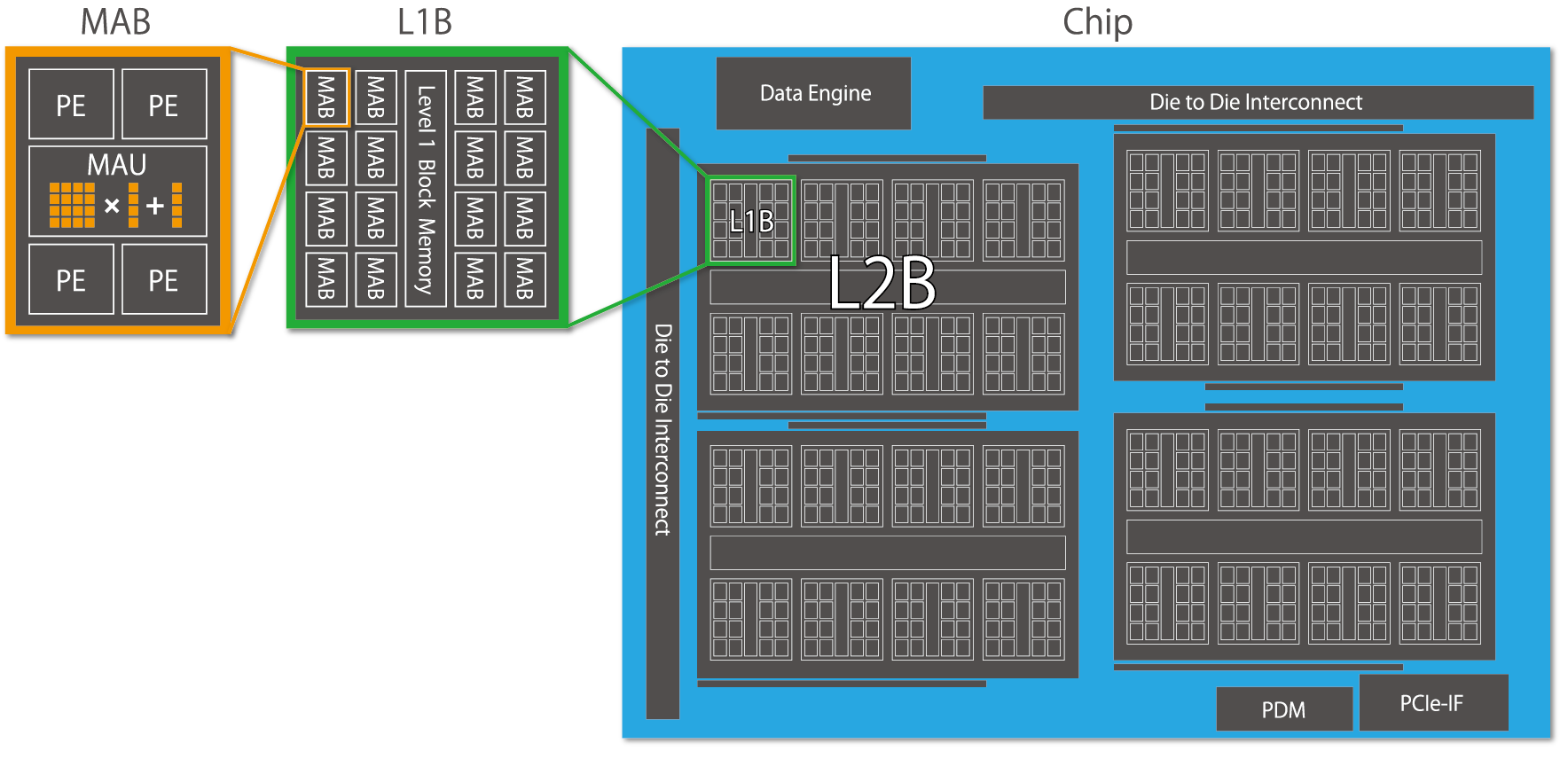
MN-Coreは以下のようなアーキテクチャ上の特徴を持っています。

• 主に演算は整数演算を行うProcessing Element (PE) と行列積和演算・ベクトル積和演算を行うMatrix Arithmetic Unit (MAU) により実行される。1つのMAUは4つのPEに共有されている。
• 階層的な構造により多数の演算器を束ねる。ボード内にChip・L2B・L1B・MAB・PE / MAUの階層を持ち、各階層間は縮約/放送などの集団通信を行うことができる。
• 単一の命令で複数の計算ユニットを動作させるSingle Instruction Multiple Data (SIMD) モデルである。その中でも条件分岐が無く、特に並列性を重視している完全SIMDモデルを採用している。
• 各PEはローカルにSRAMを持つ。一般的なプロセッサではハードウエアが制御するキャッシュをソフトウェアで陽に記述する。

このようなアーキテクチャをとることでMN-Coreは非常に多くの演算器を集積し、高い理論性能・電力効率を実現しています。

詳細や過去のインターンについては以下を参照ください。

• K. Namura et al., “MN-Core – A Highly Efficient and Scalable Approach to Deep Learning,” 2021 Symposium on VLSI Circuits, Kyoto, Japan, 2021, pp. 1-2, doi: 10.23919/VLSICircuits52068.2021.9492395.
• PFNの深層学習用スーパーコンピュータMN-3、39.38GFlops/Wの電力効率を記録しGreen500ランキングで3度目の世界1位を獲得
• MN-Core 向けの FFT の実装
• JAX から MN-Core を利用する
• MN-Coreコンパイラに向けた最適化ヒントの自動生成

背景: BLAS 

 図1 BLASルーチンのリスト。[1]より

Basic Linear Algebra Subprograms (BLAS) は線形代数演算のデファクトスタンダードなAPI群です。図1のように基本的なベクタ・行列演算がroutineとして定義されています。計算の特性に応じた3つのLevelから構成され、Level 1にはベクタ同士の演算、Level 2にはベクタ/行列演算、Level 3には行列同士の演算が定義されています。

BLASは1970年代に提案された歴史あるAPI群ですが、現在もなおBLASを実装する意義はあります。例えばBLASは機械学習や気象予報のコアな部分で呼び出されており、富岳はじめ各スパコンで実装されています。また、Linear Algebra PACKage (LAPACK) ではBLASを組み合わせてより高度な問題である連立一次方程式や固有値問題の解法を実装しています。身近な例ではPythonのNumPyやR、GaussianでもBLASをインターフェースとして用いています。

BLASはAPIの定義であり、実装が複数存在することも特徴です。例えばOSSのOpenBLAS、ATLAS、NVIDIA GPU向けのcuBLASやIntel MKLなどが代表的です。NumPyではBLASの実装としてOpenBLASやIntel MKLを選択できます。

>>> numpy.show_config()
blas_opt_info:
    libraries = ['openblas', 'openblas']
    library_dirs = ['/opt/homebrew/opt/openblas/lib']
    language = c
    define_macros = [('HAVE_CBLAS', None)]

モチベーション

MN-Coreは深層学習アクセラレータとして知られていますが、行列演算器を持つアーキテクチャ・Green500の実績などからHPCや科学技術計算の適性を持つと言えます。今回のインターンでは線形代数演算の標準的なAPIであるBLASを実装することで、科学計算の分野に対するスタンダードなインターフェースとベンチマークを与えることをモチベーションとしています。

MN-Coreの性能を活かすためにソフトウェアに求められること

MN-Coreを高効率に利用するためには、アーキテクチャを活かす適切なプログラムを与えることが非常に重要です。ここではプログラムに求められることとして2点取り上げます。

まず1点目に、大量に存在するMAU(行列積和・ベクトル積和演算器)を効率的に利用することです。MAUは1サイクルで倍精度4×4の行列と4次元のベクトルのFused Multiply-Add (FMA) を行います。このMAUがボードあたり2048個存在し、SIMDとして動作します。プログラムから並列性を抽出し、大量のMAUに偏りなくデータを供給し続けることが必要です。　
　またベクトル演算を集約して行列演算を抽出することも効果的です。MAUをベクトル積和演算モードで用いると、仮に常にMAUが動いているようなプログラムであっても、ピーク性能の1/4が性能の上限になってしまいます。
　他には、MN-Coreに限った話ではありませんが、Read After Write (RAW) にも気を付ける必要があります。これはMN-Coreの場合だとSRAMのポート数の制限により、Write命令発行の後、書き込みが完了するまでReadが実行できず生じるハザードです。nopが挟まってしまい、nopの数に応じて性能が1/2, 1/3, …と下がってしまいます。BLASは出力データを入力データと同じメモリに書き戻すinplaceなroutineが多くあるため、一旦よりポートの多い（が容量の小さい）レジスタファイルに書き出すなどで対処します。

2点目はデータ移動を減らすことです。先述した通りMN-Coreは階層的な構造を取っており、異なるブロックに存在するデータにアクセスするには追加の命令が必要となり、コストが非常に大きくなってしまいます。BLASでは行全体や列全体をなめる処理が入るため、行列の分割レイアウトを工夫し、Reductionを利用して、最小限のデータのやりとりで収まるように設計する必要があります。インターン中はデータレイアウトのことばかり考えていました。

実装

実装はMN-Coreコンパイラを用いて行いました。MN-Coreコンパイラは入力としてONNXを受け取り、MN-Coreの機械語を出力します。コンパイラは抽象度の異なるL1IR –  L3IRから構成されており、これらのIRを組み合わせてBLASの各routineを実装しました。コンパイラの詳細はMN-Coreコンパイラを用いた深層学習ワークロードの高速化を参照ください。

実装例として、Level2のGeneral Matrix Vector Multiply (GEMV, y = αAx + βy) を取り上げます。まずはデータのレイアウトを考えます。例えば入力データを図2のように分配するとします。オレンジ色の枠が各PEに割り当てられる領域です。Aの縦軸(長さm) に対して処理は完全に並列です。対して横軸(長さn)に対しては横軸全体で積の結果を足し合わせるというReductionの処理が入ってきます。問題サイズを大きくするには横軸の分割も必要であるため、Reductionのオーバーヘッドの少ない階層で分割することにします。ここでは数個に分割しましたが、実際には8192個あるPEに分割します。このようにデータをどう分割するかをレイアウトとしてコンパイラに指示しておきます。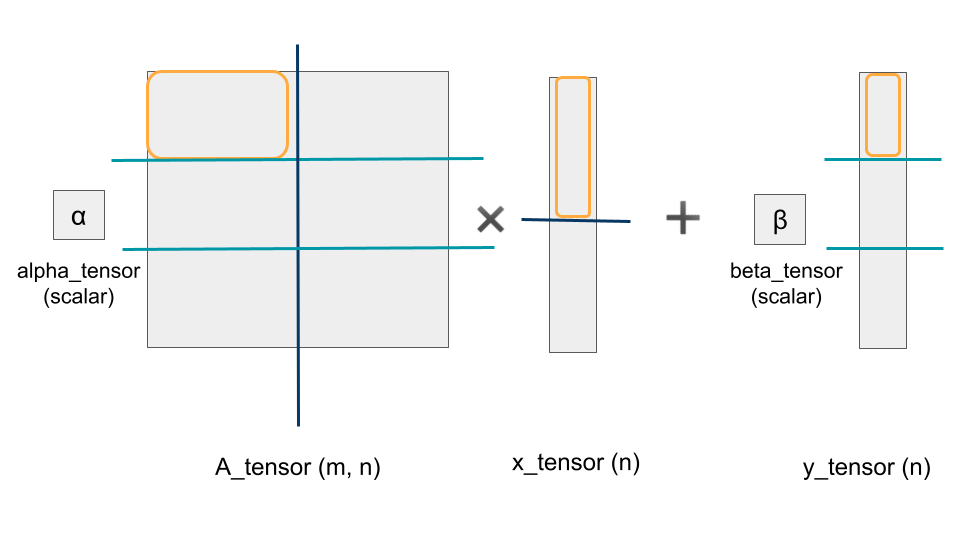図2 GEMVのデータレイアウト例

続いて各PE毎の処理を記述します。図3にGEMVの処理を出力する関数を示します。Elementwiseの処理もReductionの処理もある程度の抽象度を持って記述できます。

図3 MN-Coreコンパイラを用いた、GEMVの処理を出力する関数

評価

いくつかのBLAS routineの性能評価を紹介します。

性能の評価指標としてはFLOPSを用いています。これは1秒間の間に何回浮動小数点演算を行ったかを示す数値で、高いほど良い結果であると言えます。得られたFLOPSと、MN-Coreのピーク性能を比較します。ピーク性能はMN-Coreの全てのMAUがフル稼働した場合に得られるFLOPSです。図4には4つのroutineを取り上げ、横軸に問題サイズ、縦軸にピーク性能に対するefficiencyを示しています。値が1に近いほど演算器をフル稼働できていると読み取れます。

実験の条件としては、各入力データがPE近くのSRAMに乗っている状態を想定しています。ホストからデバイスの転送、デバイス内のDRAMからSRAMへの転送時間は計測対象に含めていません。これはMN-CoreはSRAMを大きくして再利用性を高めており、再計算を利用してDRAMアクセスを最小にする設計思想であるためです。また、各routineは倍精度で実行しています。

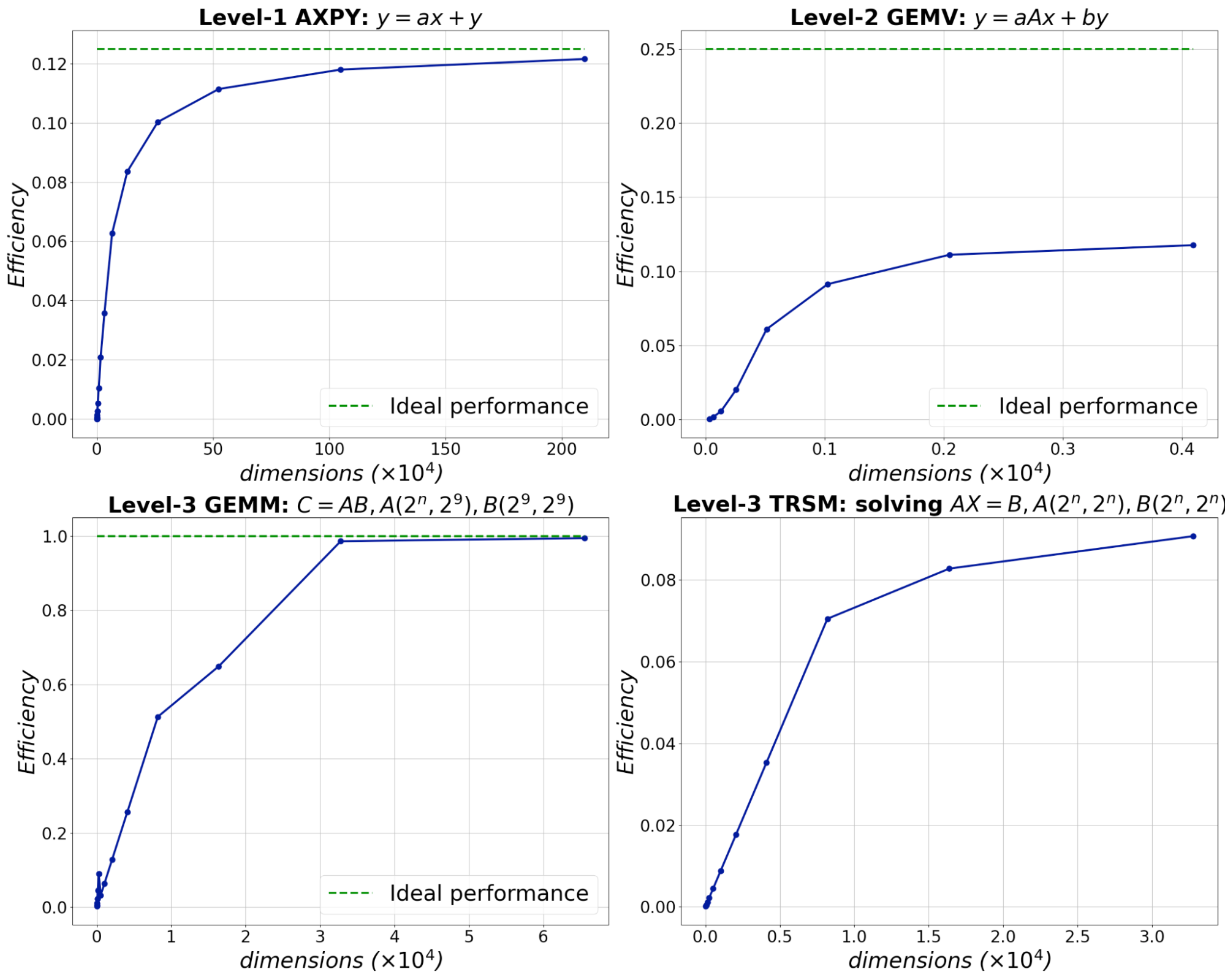
図4 DAXPY, DGEMV, DGEMM, DTRSM実装の問題サイズに対するefficiency

　ピーク性能と比較するとLevel1 AXPYは1/8, Level 3のGEMMはほぼ1/1の性能で収束しており、これらは各routineに対する上限値が出ていると考察しています。Level1のroutineはベクトルのinplaceな書き戻しに律速されています。Level 2は行列演算器に対してベクトルを与えて計算しているため1/4で律速されています。Level 3 GEMMは適切なサイズの問題ではほぼ常に行列演算器が稼働し、ほとんどピークに近い性能が得られています。このGEMMの実装は既にMN-Coreコンパイラに実装されていたもので、実際に社内の学習のワークロードでも80-90%のピークに対する効率が出ていることが確認されています。
　ただ上限値が出ていないroutineもありました。例えばLevel 2 のGEMVは積と和がバランスしておらず、FMAが使えていません。Level3のTRSMという三角行列の係数行列に対する行列方程式を求めるroutineは、そもそもTRSMが前進・後退代入の逐次的な演算である・上手く行列演算に落とし込めていない・重複してデータを持たせているといった理由があります。また全Levelに共通することとして、問題サイズが小さい場合は、SIMDで意味のない計算が走っていることになり、理想的な性能は実現されません。実際の運用ではバッチ化[2] するなどの対応が考えられます。
　図5には残りのいくつかの倍精度routineについて、問題サイズに対するefficiencyを示します。

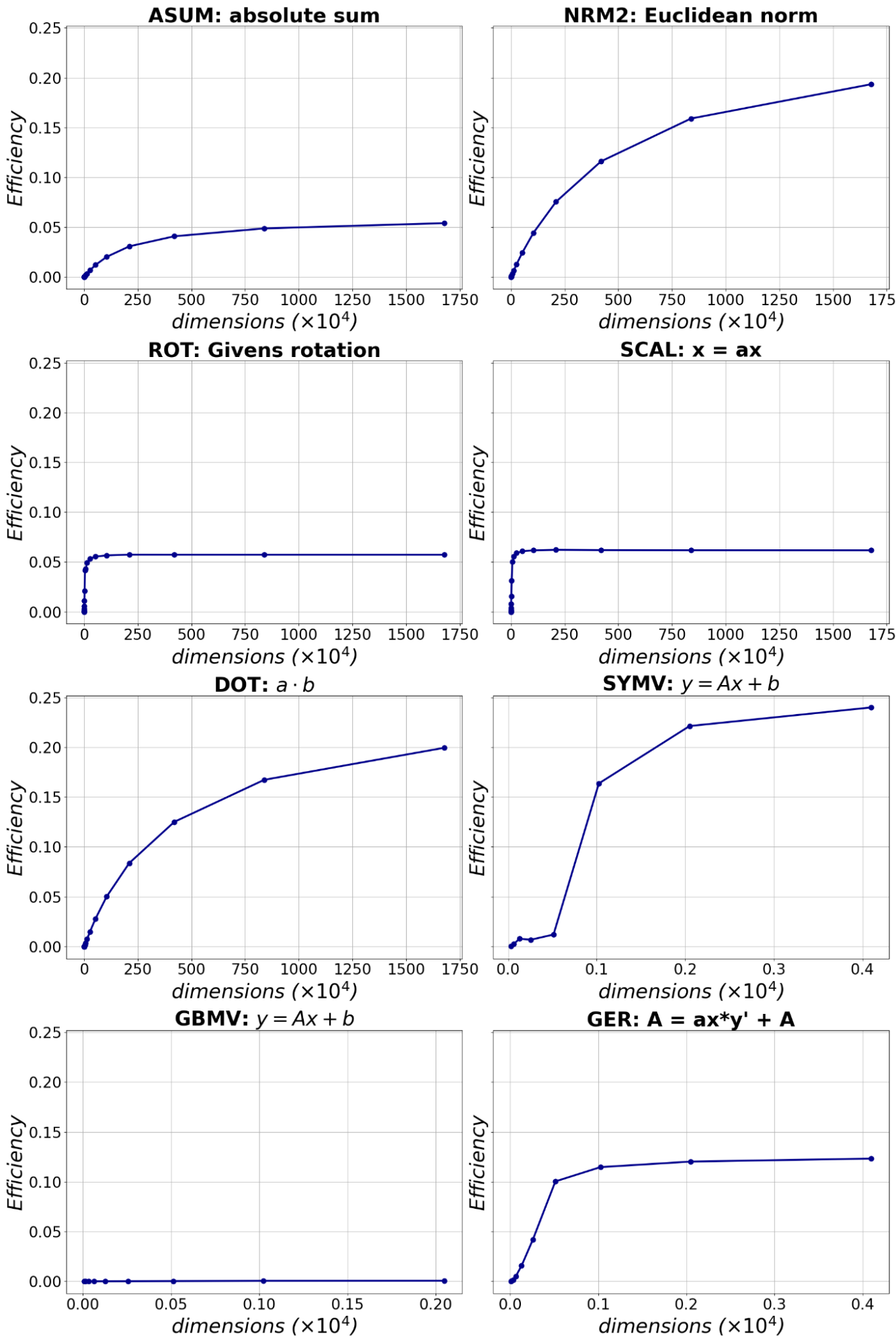
図5 その他の倍精度routine実装の問題サイズに対するefficiency

まとめ

今回のインターンではMN-Core向けにBLASを実装しました。
ハードウエアを活かすプログラムとは何なのか、命令列レベルで考えてプログラムを書くということを学び、非常に楽しいインターンでした。
最後になりましたが、メンター・サブメンターをしていただいた井町さん・樋口さん・河田さん、そしてコンパイラチームの皆さんには沢山のことを教えていただき、大変お世話になりました。この場を借りて御礼申し上げます。

参考文献

[1] Netlib: BLAS(Basic Linear Algebra Subprograms)
[2] Batched Conv