Blog
本記事は、2022年度PFN夏季インターンシップで勤務された諸戸雄治さんによる寄稿です。
2023年4月21日 追記
本成果を第188回ハイパフォーマンスコンピューティング研究発表会にて発表いたしました。原稿は http://id.nii.ac.jp/1001/00225069/ に収録されています。
はじめに
2022年度夏季インターンに参加させていただいた、諸戸雄治です。
学部時代は HPC 系研究室に、現在はコンピューターグラフィックス系の研究室に所属し、CGで使われるアルゴリズムの計算量改善や、AVX や CUDA を用いた高性能な実装の開発などに取り組んでいます。また私の執筆した離散フーリエ変換(DFT)についての記事は「離散フーリエ変換」や「DFT」と検索すると上位にヒットする人気記事となっています。
今回のインターンでは、PFNの所有するスーパーコンピュータ MN-3 に搭載されているアクセラレータ MN-Core™で動作する、高速フーリエ変換(FFT) の実装に取り組みました。
MN-Core の概要とFFT
深層学習を軸とする研究開発には計算資源を多く要します。そこで PFN はこの計算を得意とするアクセラレータ MN-Core を神戸大学と共同開発し、実際にスーパーコンピュータMN-3に搭載して運用しています。MN-3は極めて高い省電力性能を持ち、スーパーコンピュータの省電力性能ランキングGreen500で世界1位を3度獲得しています。
MN-Coreは深層学習ワークロードに特化したアクセラレータです。アーキテクチャとして以下の特徴を持っています。
- 単一の命令で複数の計算ユニットを動作させるSIMD(Single Instruction Multiple Data)モデルの、その中でも条件分岐が無く特に並列性を重視している完全SIMDモデルを採用している
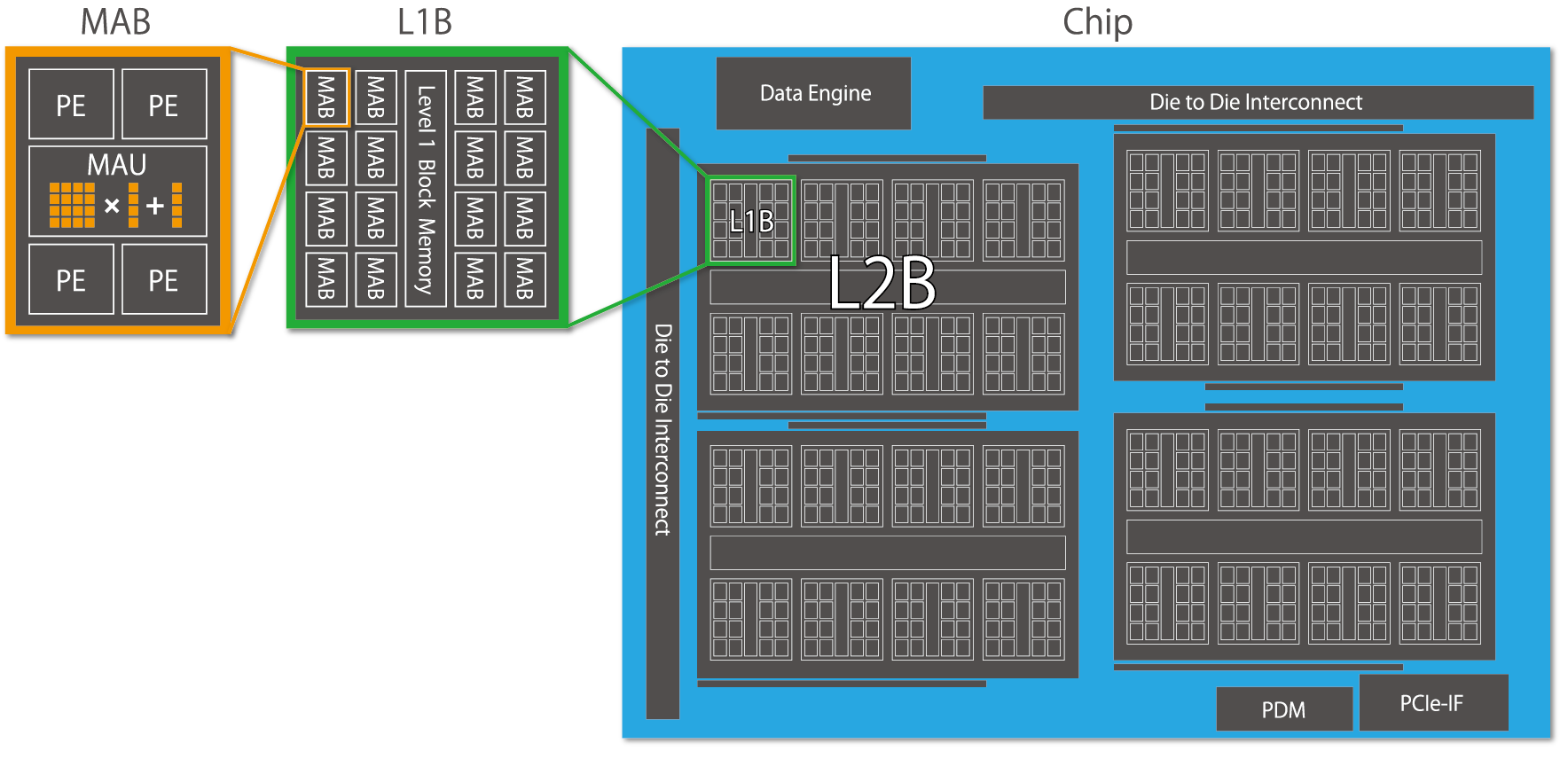
- 1 Package (Board) の中に Chip, L2B, L1B, MAB, PE と階層的な構造を持っており、同じ命令を演算器間で同期して超並列計算とデータ移動を行う
- チップ内に SRAM、基板に DRAM が搭載されており、一般的なプロセッサではハードウェアが自動的におこなう様なキャッシュは存在せず、データ移動の制御をソフトウェアで陽に記述する
- ハードウェア制約の許す限りで単一の命令内に複数種類の処理を指示でき、それらが同時に実行されるモデルを採用している
- 主に演算は、1MABあたり4個ある PE による整数演算器と、MABあたり1個のMAU(行列演算ユニット)での浮動小数点・行列積演算器で行う。特に高いピーク演算性能を持つ行列積演算ユニットを効率的に使用できるかが重要
これらのアーキテクチャ上の特徴を活かすことで、MN-Coreは演算器の配置において極めて高い集積性を実現し、他のプロセッサを超えた計算性能・電力効率を実現しています。

離散フーリエ変換 (DFT)
離散フーリエ変換とは、長さ \(n\) の複素数配列 \(X\) を入力に、以下の手順で長さ \(n\) の複素数配列 \(F\) を出力する計算です。
\[
F[a] = \sum_{b=0}^{n-1}X[b]e^{-2i\pi ab/n}
\]
ここで \(e\) はネイピア数であり、\(i\)は虚数単位です。入力として複素数配列を要求しますが、虚部が0である実数配列を入力として構いません。
この計算で得られる \(F\) によって、\(X\) の周波数成分を抽出することができます。具体的には、1周期の長さが \(n\) の正弦波が強さ \(p\) で \(X\) に含まれていた場合\(F[1] = p\) と、1周期の長さが \(n/4\) の強さ \(q\) の正弦波の場合 \(F[4] = q\) と得ることができます。詳しい原理についてはこちらの記事 [1] をご覧ください。
この計算は数式通りに計算すると、長さ \(n\) のデータに対して \(O(n^2)\) の時間がかかってしまいますが、これを \(O(n \log n)\) の時間で計算する手法が高速フーリエ変換(FFT) です。
音声信号処理の場合、0.1秒など短時間の間に含まれる特定の周波数成分のみを抜き出したり、100Hz以下の低周波のみを抽出したいなどのローパスフィルタなどの用途があります。
画像処理の場合は入力が2次元配列となりますが、水平方向と垂直方向でそれぞれ独立に離散フーリエ変換を行うことで周波数成分の抽出を行うことができます。
これらの用途の場合、複数の独立したデータ列を一度に離散フーリエ変換する必要があります。例えば10秒の音声を0.1秒単位で解析しようとした場合は100個の独立したデータに処理をする必要があり、256×256 ピクセルの画像の場合は、長さ256の独立した256本のデータを処理することになります。かくして信号解析では複数のデータ列を同時に処理する必要があり、CUDA の公式 FFT ライブラリ cuFFT などでは長さ n の他に、同時に計算するバッチ数も指定して処理させることができます。
この様に離散フーリエ変換は、音声や画像データに含まれる高周波や低周波などの周波数成分の抽出に使用することができます。また周波数成分の解析の他にも、実領域では時間のかかる計算をフーリエ領域を介して計算をすることで、効率的な計算が可能になるものもあります。例えば畳み込み定理を利用することで、長さがそれぞれ n と m のベクトルの畳み込みが、実領域でそのまま計算すると \(O(nm)\) の時間がかかるところ、フーリエ空間では \(O(n+m)\) で計算可能なことが知られています。この場合、計算量としては FFT にかかる \(O((n+m)\log (n+m))\) で畳み込みが計算可能なります。
更に、MN-Core は ONNX により表現された計算グラフであれば、演算が対応していれば計算可能なため、深層学習以外の用途でも使用可能です。今年のインターンでは前川隼輝さんが、NumPy ライクなライブラリである JAX から MN-Core を利用するためのコンパイラ及び周辺ライブラリの開発に取り組みました。これによりJAX から MN-Core を利用できるようになり、深層学習以外のワークロードを比較的容易に MN-Core 上で試せるようになりました。例えば物理シミュレーション分野では3次元の離散フーリエ変換が必要な場面もあり、FFT が GPU による計算のボトルネックになることがあることから、MN-Core の極めて高い省電力性能が利用可能になることが望まれています。
高速フーリエ変換 (FFT)
単純に離散フーリエ変換を行うと \(O(n^2)\) の時間がかかってしまいますが、DFT の係数として用いる \(e^{-2i\pi ab/n}\) の規則性と、\(e^{2i\pi} = 1\) という性質を用いることで、\(O(n \log n)\) の時間でDFTを計算することができます。特に \(n\) を素因数分解したとき、小さな素数のみからなる場合、効率的に計算可能です。今回は \(n\) が2のべき乗であるとして実装しました。
下記のシグナルフローグラフは、\(n=16\) の場合の高速フーリエ変換の過程を示したものです。
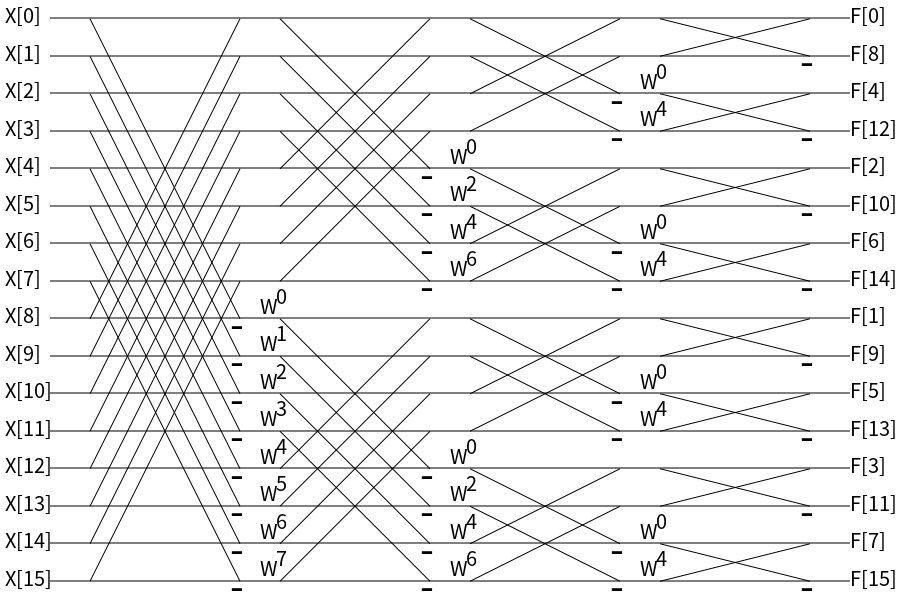
図中の \(w\) は、 \(w = e^{-2i\pi/n} = \cos(-2i\pi/n)+i\sin(-2i\pi/n)\) とします。左の \(X\) が入力であり、右に向かって演算を行い、右端の\(F\) が出力です。 2線が合流するところは加算を、合流地点に「-」が書かれているものは減算を意味します。線上に \(w\) が書かれている場所は値を \(w\) 倍します。
以下の図は、わかりやすくある2線を抜粋して簡略化して記したものです。この図が蝶の姿に似ていると言う理由から、バタフライ演算と呼ばれています。
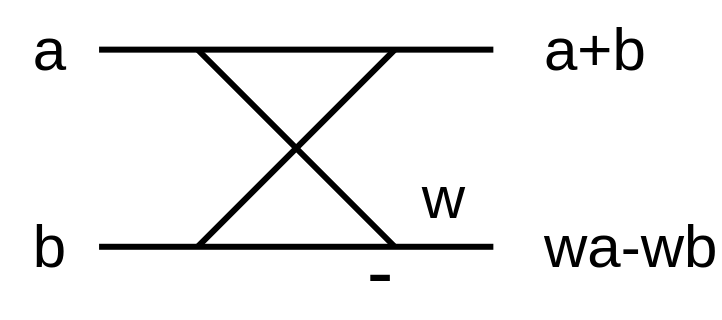
FFT はこのバタフライ演算を規則的に組み合わせることで、\(O(n \log n)\) の時間で計算を実現させています。
注意として、最後の出力配列の添字に着目すると順番が変わってしまっています。これは2進数で見たときにビットの上下が反転した順序になっています。つまり、2進数は 0から順に 0000, 0001, 0010, 0011, 0100, … と表現されますが、ビットの上下を反転させた 0000, 1000, 0100, 1100, 0010, … という順序になっており、Cooley-Tukey 型 In-place FFT で実装した場合に発生します。基本的にこのままでは不都合なので、最後に並び順を修正するか、Stockham 型 self-sorting FFT で実装することで回避可能です。
行列積計算ユニットとFFT
今回のインターンでは MN-Core の MAB レベルでの並列化で解く FFT を実装しました。つまり、1本あたりのFFTを、4つのPEと1つの行列演算ユニットで適切なデータ移動・演算をさせて解きます。
想定する FFT される配列の長さ \(n\) は 16〜8192 程度(特に 64〜512 あたり)、そして大量のバッチ数のデータを同時に処理するとします。例えば 512 枚の 3チャンネル 64×64 の画像を同時に FFT をする場合、\(n=64\), バッチ数\(b=64\times 3 \times 512 = 98304\) となります。1 Board で処理する場合、1 Board あたり 2048 個の MAB があるので、このとき 1 MAB あたり 48 バッチ担当する事になります。
16個のMABで連携し L1B レベルで1つの問題を解くことも考えられ、この場合 1つの MAB の SRAM に載らないほど大きなサイズ(\(=n\))の問題を解くことが可能になります。しかし MAB 間のデータ通信帯域の制約の関係から PE 間通信ほど自由が効かないため、各 MAB で独立した問題を解くことにします。今回のインターンでは各 MAB 独立状態で \(n=1024\) まで、\(nb=4096\) までの問題を解くことができました。
冒頭の概要でも触れたとおり、MN-Core の特色は高性能な行列演算であり、倍精度であれば4×4 の行列積の形に演算を変形することが目標になります。ここで、行列×行列積のまま考えるのは問題が難しくコーナーケースも増えるため、4バッチを同時に計算することにして実装しました。説明では 4×4行列 と 1×4 ベクトルの積として説明します。
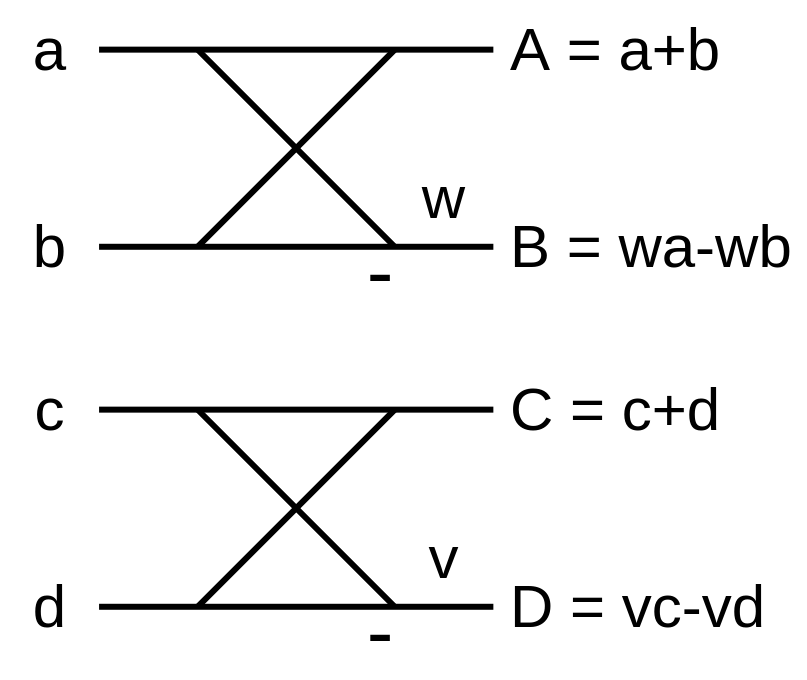
上のような 2つのバタフライ演算を同時に行列・ベクトル積演算として表現すると、以下のようになります。
\[
\begin{pmatrix}
A\cr B\cr C\cr D
\end{pmatrix} = \begin{pmatrix}
1 & 1 & 0 & 0 \cr
w & -w & 0 & 0 \cr
0 & 0 & 1 & 1 \cr
0 & 0 & v & -v \cr
\end{pmatrix} \begin{pmatrix}
a\cr b\cr c\cr d
\end{pmatrix}
\]
4×4行列のうち、半分が 0 なので明らかに非効率そうです。更に、入出力や行列は複素数なので実虚それぞれで計算する必要があり、2組のバタフライ演算を計算するのに4回の行列演算が必要になります。
\(a, b, c, d\) の2組4要素ではなく、\(a,b\)の1組2要素だけに注目し、\(a\) の実部を\(a_r\)、虚部を\(a_i\)として行列演算させることを考えると、以下のようになります。
\[
\begin{pmatrix}
A_r\cr A_i\cr B_r\cr B_i
\end{pmatrix} = \begin{pmatrix}
1 & 0 & 1 & 0 \cr
0 & 1 & 0 & 1 \cr
w_r & -w_i & -w_r & w_i \cr
w_i & w_r & -w_i & -w_r \cr
\end{pmatrix} \begin{pmatrix}
a_r\cr a_i\cr b_r\cr b_i
\end{pmatrix}
\]
比較的密な行列になりました。一気に実部虚部の計算が可能なため、1回で1組2要素のバタフライ演算が完成します。しかし、MN-Core では \(A_r, A_i, B_r, B_i\) と要素を読み書きするのは追加コストがかかってしまうため、効率的な実装が難しくなってしまう難点があります。
さて、ここまで紹介してきたものは 基数 2 のバタフライ演算と呼ばれるものですが、2段4要素を一度に考える基数 4 のバタフライ演算 [2] を考えます。
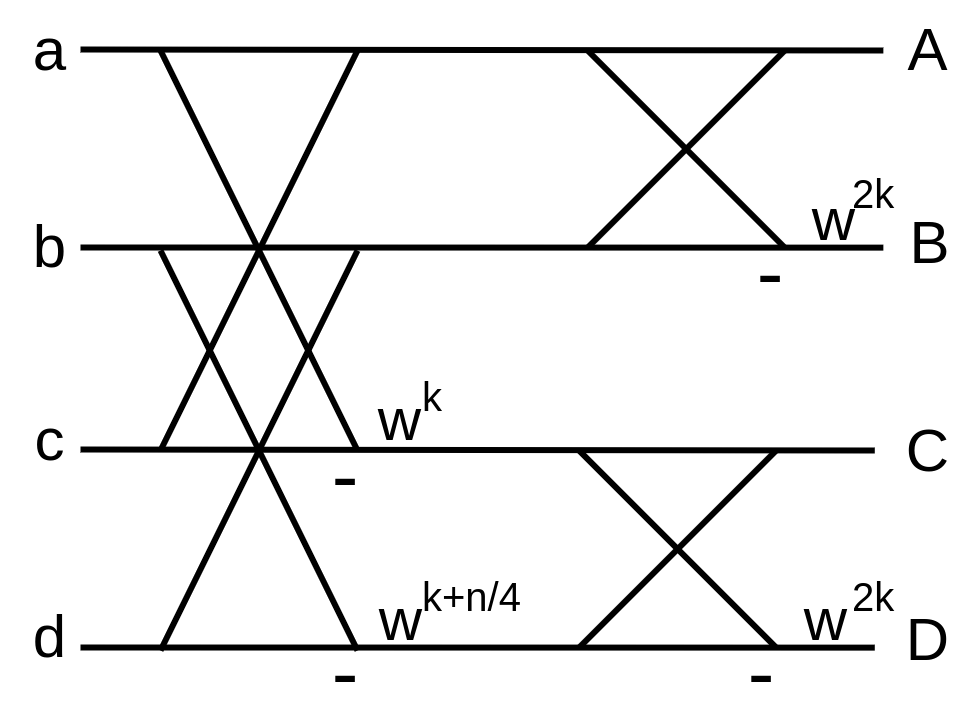
行列演算を用いない一般的なアーキテクチャでは、\(w^{n/4} = i\) という性質を利用して変形することで乗算回数を 3/4 に減らせ、また必要なメモリの Load/Store 数も減らせることが知られています。AtCoder 社が提供する競プロ用アルゴリズムライブラリ AC Library の FFT の実装でもこの基数4 の FFT が採用されており、基数 2 より高効率であると報告されています。
しかし今回の行列演算では、Add も FMA も同コストであるので、単純に 2 段同時に計算できるというメリットだけに着目します。その場合、以下のような行列計算になります。
\[
\begin{pmatrix}
A\cr B\cr C\cr D
\end{pmatrix} = \begin{pmatrix}
w^0 & w^0 & w^0 & w^0 \cr
w^{2k} & -w^{2k} & w^{2k} & -w^{2k} \cr
w^{k} & w^{k+n/4} & -w^{k} & -w^{k+n/4} \cr
w^{3k} & -w^{3k+n/4} & -w^{3k} & w^{3k+n/4}
\end{pmatrix} \begin{pmatrix}
a\cr b\cr c\cr d
\end{pmatrix}
\]
密な行列になりました。\(w^0 = 1\) であり、またこの虚部は0であることを考えると改善の余地がある気もしますが、今まで一番密な行列でしょう。この場合も実虚でそれぞれ演算が必要になるので、2組2段のバタフライ演算を4回の行列演算で計算することになります。先程の1組1段のバタフライ演算を1回の行列演算で行う方法と比べると効率は同じですが、2組2段の方はデータのLoad/Storeの相性も良く、更に行列の内容を計算する回数が減るため、効率的にバタフライ演算が可能になります。
基数 4 の FFT の場合、\(n\) が 4のべき乗のみの対応になりますが、\(n=4^k \times 2\) の場合は最後に基数2のFFT を行うことで2べきの\(n\)に対応可能です。このときの最後の基数2のFFTでは行列の値が複素数ではなく実数になるため、実部と虚部で独立して計算できます。
評価
今回実装した FFT の性能を評価するために、いくつかの実験を行いました。
まず GPU との比較として、\(n=256\) に固定して CUDA の公式 FFT ライブラリ cuFFT と比較実験を行いました。GPU は NVIDIA Tesla V100 を使用しました。cuFFT は倍精度・単精度両方に対応しているので両方の実験を行いました。MN-Core 側は 1 Board あたり 32768 バッチまで同時に計算可能です。GPU のバッチ数は MN-Core と同じ 32768 バッチのときの値と、単位時間あたりに処理できたバッチ数(Throughput)が最も良かった 1,048,576 バッチのときの値で評価します。実行時間と Throughput の結果は以下の通りです。
\[
\begin{array}{l|rrr}
&\text{Batch/Board}&\text{Time(ms)}&\text{Throughput(Batch/ms)}\\
\hline
\text{MN-Core (倍精度)} & 32,768 & 0.049 & 668,735 \\
\text{V100 (倍精度) } & 32,768 & 0.350 & 93,623 \\
\text{V100 (倍精度) } & 1,048,576 & 10.439 & 100,447 \\
\text{V100 (単精度) } & 32,768 & 0.184 & 178,087 \\
\text{V100 (単精度) } & 1,048,576 & 5.227 & 200,608 \\
\end{array}
\]
V100 の倍精度と比較して、6〜7 倍以上の Throughput が達成できました。また、今回のインターンで実装した FFT は倍精度のみですが、単精度で良い場合でも V100 の単精度と比較し 3 倍以上の性能が達成できました。
V100 の結果について考察すると、倍精度 1,048,576バッチのときを考えると 256(N) x 1Mi (Batch) x 2 (実部, 虚部) x 8Byte (double) x 2(往復) = 8GiB のデータのやり取りが行われ、V100 のメモリバンド帯域幅900GB/sでは約9msかかることから、メモリバンド幅律速であることが考えられます。FFT の計算量は \(O(n \log n)\) と比較的軽い計算であり、一般にメモリバンド幅律速になりやすい計算と言えます。MN-Core の結果に関しても、\(n=256\) に対して 1 Board に対して 32,768 を超えたバッチ数を処理させたい場合、SRAM に載らなくなるので DRAM と通信する必要があり、メモリバンド幅律速になることが予想されます。これを回避・軽減するためには、FFTの前後の演算が同じか近くのバッチのデータのみで計算できるものであれば FFT と演算を Fusion、つまり DRAM 転送が不要なバッチレベルで演算を進める事によりメモリバンド幅律速を軽減できるかもしれません。
次に、MN-Core で実行する際に行列演算ユニットをどれほど稼働できたかについて議論します。MN-Core は1命令で複数レベルの演算器を同時に可動させることができ、どれほど行列演算ユニットを休まずに働かせられたかが重要になります。今回は FFT の長さ \(n\) と、1MAB あたりのバッチ数 \(b\) を変化させて、全命令のうちバタフライ演算で使用した行列演算命令数の割合を求めました。結果は以下の通りです。
\[
\begin{array}{cc|ccc}
n & b &\text{行列演算命令数} &\text{全命令数} &\text{行列演算器稼働率(%)} \\
\hline
256 & 16 & 4096 & 5060 & 80.95 \\
256 & 8 & 2048 & 2756 & 74.31 \\
256 & 4 & 1024 & 1604 & 63.84 \\
512 & 4 & 2304 & 3396 & 67.84 \\
1024 & 4 & 5120 & 7240 & 70.72 \\
512 & 8 & 4608 & 5988 & 76.95 \\
\end{array}
\]
今回の実装の都合上、\(nb \le 4096, b\ge 4\) と言う制約が発生しています。 \(n\)を固定して \(b\) に注目すると \(b\) が大きいほど、\(b\)を固定して \(n\) に注目すると \(n\) が大きいほど効率が良いことが分かりました。これはデータ量が大きいほど、処理の初期化や行列に入れる係数の計算などバタフライ演算以外に必要な計算が占める割合が減るからです。\(nb\) を固定したときに注目すると、\(n\) が小さい方が効率が良いことも分かります。これは \(n\) が大きくなるよりも \(b\) が大きくなる方が、行列の値を使いまわししやすい影響が大きいからです。
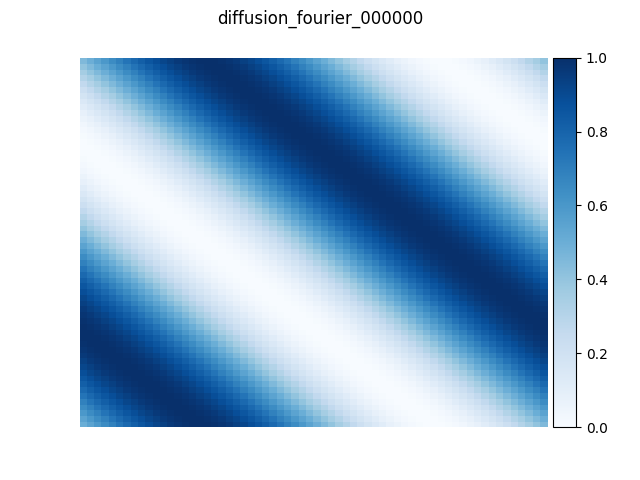
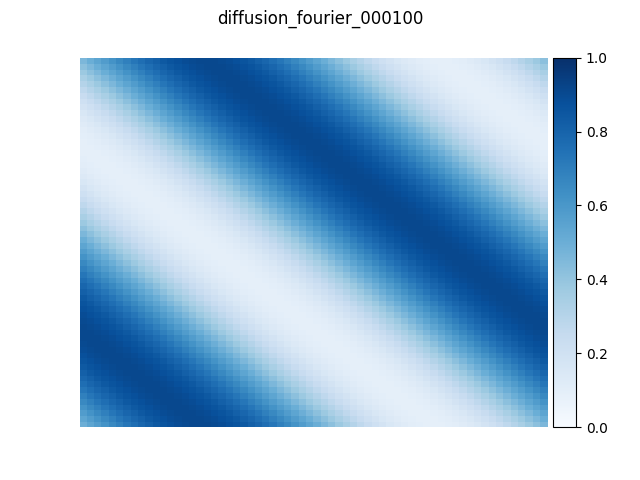
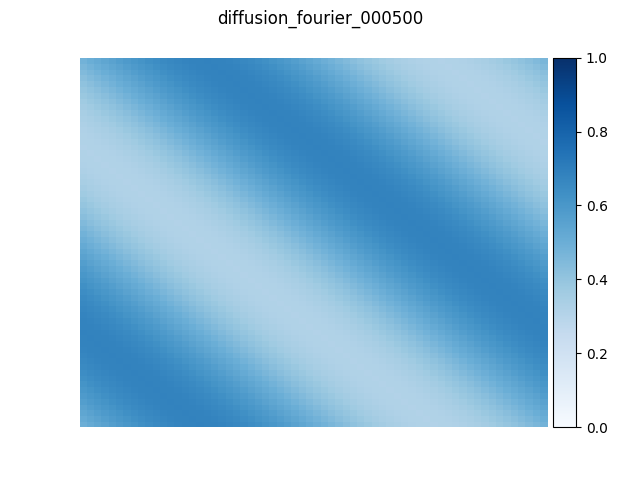
最後に、実際に Python 上から MN-Core による FFT を利用する例を紹介します。周期境界条件の2次元拡散方程式の近似解を、空間微分近似に擬スペクトル法を用いて求めました。数値計算コードはPyTorchで書かれており、過去の記事「MN-Coreコンパイラを用いた深層学習ワークロードの高速化」で紹介したコンパイラスタックでMN-Coreプログラムにコンパイルしています。以下の図は 64×64 格子サイズで、初期状態、100、500、2000時間ステップ経過した状態をMN-Coreで実行した結果です。値が一様に広がっていく様子が確認でき、解が徐々に収束していく様子が分かります。
 |
 |
 |
 |
今後の課題
今回実装した FFT は \(16 \le n \le 1024\) の範囲で対応していますが、1024 を超えたサイズの FFT も音声信号処理などで必要になることがあるので対応が待たれます。現在 MAB 内で計算が完結する範囲までしか対応していませんが、L1B に含まれる 16 個の MAB を連携・通信させることで \(n \le 16,384\) まで対応可能な見込みです。\(n = 2048\) のとき、\(2048 = 4^5 \times 2\) であり 1 複素数要素あたり \(5+1 = 6\) 段のバタフライ演算、つまり\(5\times4 + 1\times2 = 22\) 回の行列演算が必要になることから、上手く実装すれば MAB 間の通信速度に大きく足を引っ張られずに実装可能だと考えています。
また今回は倍精度の MN-Core 用 FFT しか実装しませんでしたが、単精度であれば理想的には4倍の速度が出るはずなので、単精度用の実装も今後の課題です。
まとめ
今回のインターンでは MN-Core 向けの FFT を実装しました。普段書いている CUDA などの並列プログラミングの知見が活かせたほか、性能に重点を置いて設計された MN-Core の思想に触れられて非常に刺激的でした。また行列演算ユニットが用意されたアーキテクチャは近年の CUDA でも Tensor コアがありますが、今回のインターンで行列演算ユニットの理解も深めることができ、大変有意義なインターンでした。2ヶ月弱のインターンでは MN-Core プログラミングを把握し始め、思想を徐々に理解し始めたところで終了となってしまいましたが、メンターの井町さんをはじめコンパイラチームの皆さんには本当にお世話になりました。この場を借りて御礼申し上げます。
参考文献
Area




