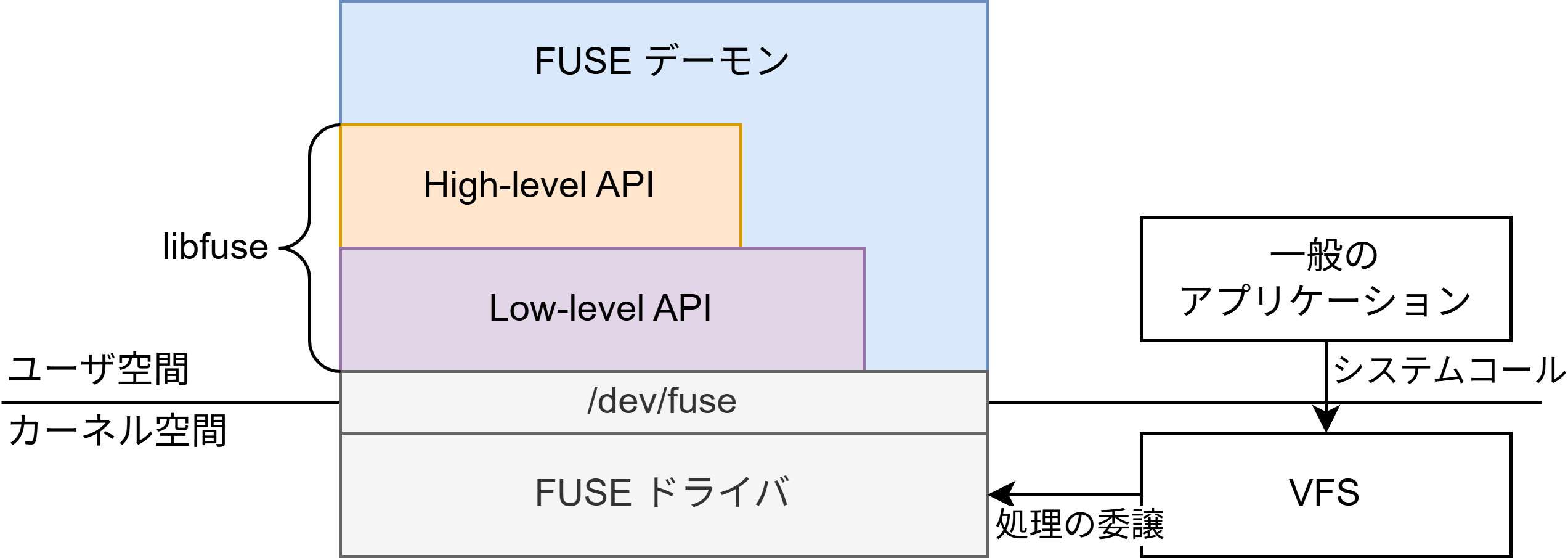
Blog
2024.10.25
Blowin’ in the Wild: バラバラに撮影された画像からの4D Gaussian Splattingの開発
Area
Sosuke Kobayashi
Researcher
はじめに
PFN2024 夏季インターンに参加させて頂きました、慶應義塾大学 理工学研究科修士1年の香山楷と申します。 大学ではコンピュータビジョン系の研究室に所属しており、普段は生物の網膜を模した新しいビジョンセンサであるイベントカメラを用いた研究を行っています。
この度は7週間研究開発インターンとして、”Blowin’ in the Wild[1]”と題しまして「動画撮影をせずとも風を感じられる4D再構成」の研究に取り組みました。本ブログではその内容について紹介させて頂きます。
まずはこちらの成果物(gif)をご覧になり、風を感じてください。

We implemented looping 4D Gaussian splatting from monocular images (not video). English slide is available here!
モチベーション
近年、三次元再構成分野が目覚ましい発展を遂げています。NeRF [Mildenhall et al. 2020]や3D Gaussian Splatting [Kerbl et al. 2023]をはじめとする微分可能レンダリングに基づく輝度場表現の登場は、今までにない写実的な3Dシーンを画像から復元可能とし、産学両方に多大な影響を与えました。
そうした3D再構成手法の進歩に伴い、より発展的なタスクである4D再構成(動的シーンの3D再構成)に取り組む研究や応用事例も熱を帯びてきています。近年の4D再構成研究の動向についてはサーベイペーパー [Yunus et al. 2024]にまとめられているほか、PFNでもスポーツなどの4D再構成やバーチャルプロダクションの背景への3D再構成活用など様々な開発が行われています。

しかし従来の4D再構成フローにおいては、撮影時に複数台のカメラをセッティングする必要があり煩雑で、かつそれぞれのカメラで動画データを記録するため扱うデータ量が膨大となる、といった課題があります。
そこで、今回のインターンでは風に揺れる被写体を1台のカメラで散発的に撮影した不規則な時間の画像から、バーチャルプロダクションの背景として使いやすいループする動きが付いた3D空間を再構成することを目標に研究開発を行いました。
このような問題設定においては、以下に挙げるような要件をクリアするシステムが求められます。
- 被写体が動く、3D再構成するにあたって理想的でない画像(”in-the-wild”画像)が入力される
-> 入力する画像ごとの被写体の動きや変形を考慮する必要がある - 動画ではなく、不規則的に撮影された画像が入力される
-> 動画と異なり密で連続的な時間情報を用いることができないため、オプティカルフローなどによる動きの定義ができない(既存の4D再構成手法の適用が難しい) - 動きがループするシーンを出力する
-> バーチャルプロダクションの背景としての利用に耐えうる、切れ目のわからない自然な動きを表現する工夫が必要
1台のカメラで4D再構成を行う単眼手法自体はこれまでにも提案されていますが、密で規則的な撮影データを用いず、かつループするシーンを出力するという問題設定は、知る限りではまだ取り組まれていない新規のものになります[2]。 以下に、これらの問題を解くために行った工夫とその評価実験を紹介します。
In-the-Wild手法に基づく4D Gaussian Splatting
今回は3D空間表現として、冒頭でも触れた3D Gaussian Splatting (3DGS)を用いました。これはシーンを3Dガウシアンの集合として表現する手法で、比較的少ない計算量で写実的な3D再構成が可能です。 個々のガウシアンは位置や回転・色などの学習可能パラメータを持っており、再構成したい物体を撮影した複数の観測画像と、ガウシアンで表現したシーンのレンダリング結果が近づくようにパラメータ更新を行うことで、シーンを学習します。
一般的な3DGSの訓練時の入力としては動きがなく、かつ照明環境等も変化しない静的な画像が要求されますが、被写体の照明環境が変化するようなin-the-wild画像を扱うための3DGS手法も提案されています。WildGaussian [Kulhanek et al. 2024]では、通常の3DGSに学習可能なパラメータとして入力画像ごとのembeddings、ガウシアンごとのembeddingsとMLPを追加し、レンダリング時に画像ごとの各ガウシアンの色の変化量を推定します。それにより、昼間の画像や夜間の画像など照明環境が異なる入力に対しても、照明環境をパラメータとして操作可能なシーンを再構成可能となることが報告されています。
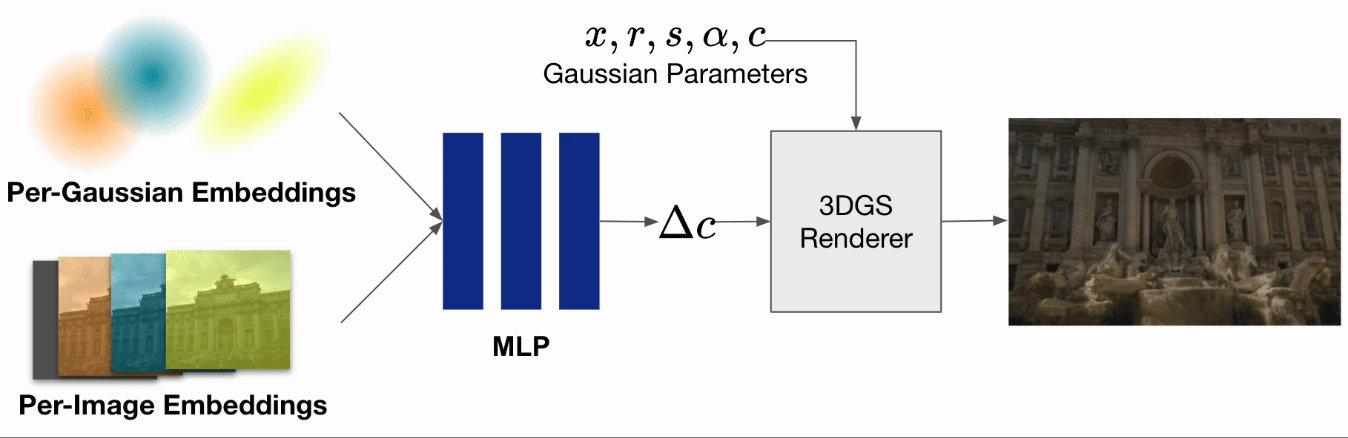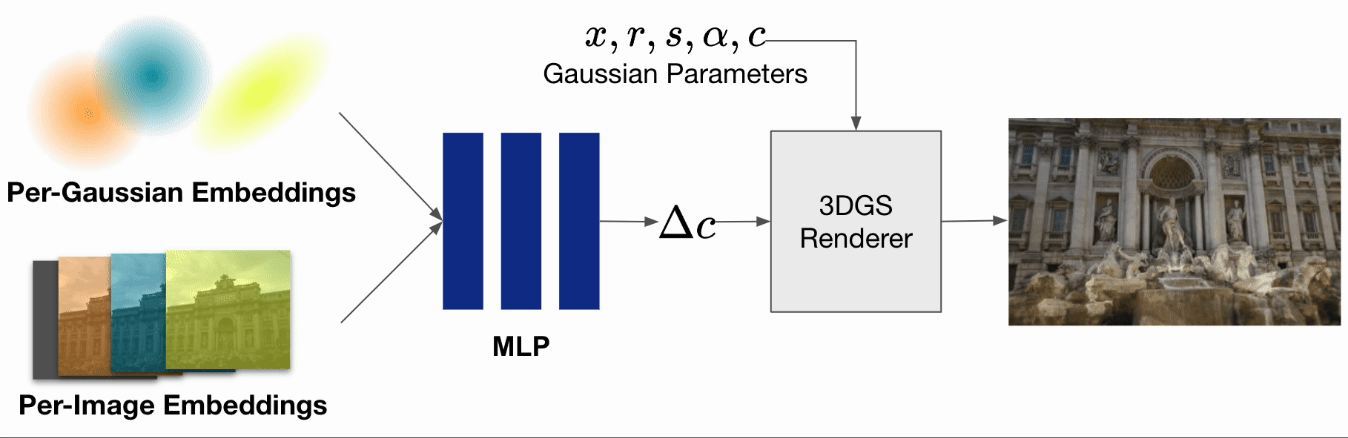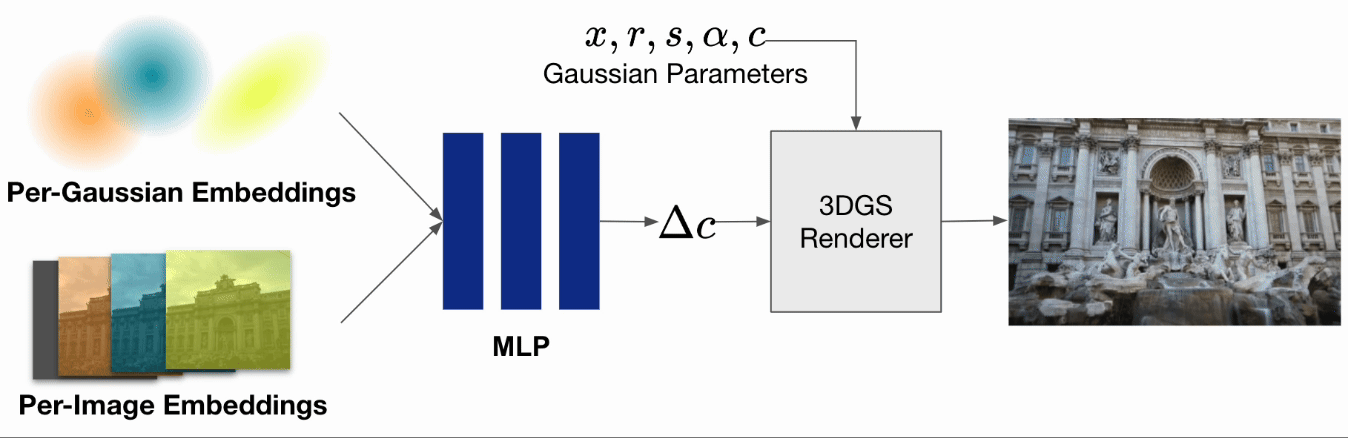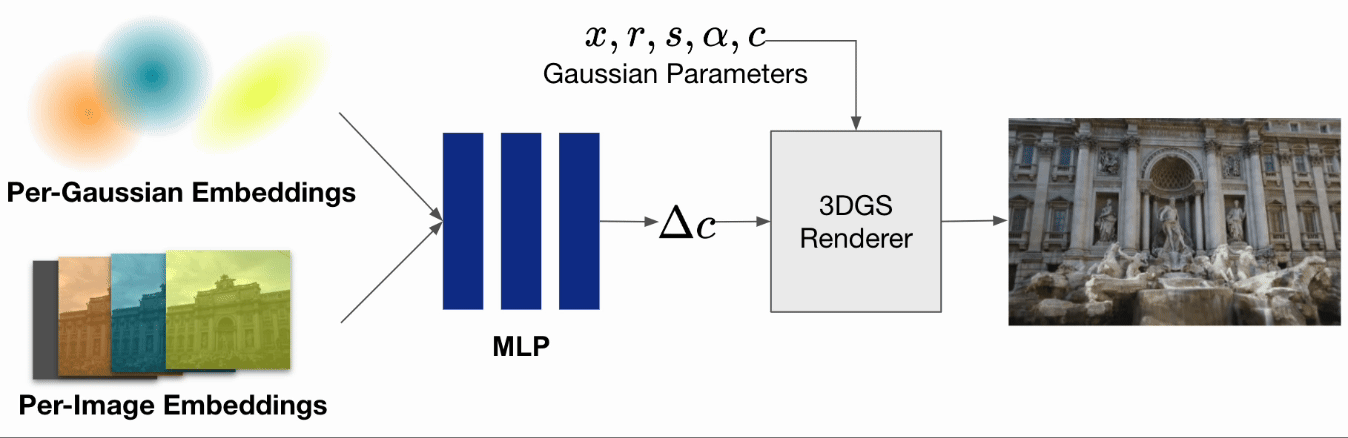
WildGaussianでは建造物を様々な時間に撮影した画像を対象にしていました。 一方で今回の問題設定では、昼や夜など照明環境が大きく変わることはない代わりに、各画像ごとにシーン内の被写体が移動・変形している可能性があります。
そこで本インターンではWildGaussianをベースに、embeddingsによって各ガウシアンの色の変化量ではなくガウシアンの移動量・回転量を学習させることで、動的なシーンの再構成を試みます。WildGaussianではembeddingsとMLPによって異なる照明条件の色の表現を自動で獲得できたのと同様に、入力画像ごとに少しずつ位置が異なる被写体から動きの表現を獲得することが期待されます。
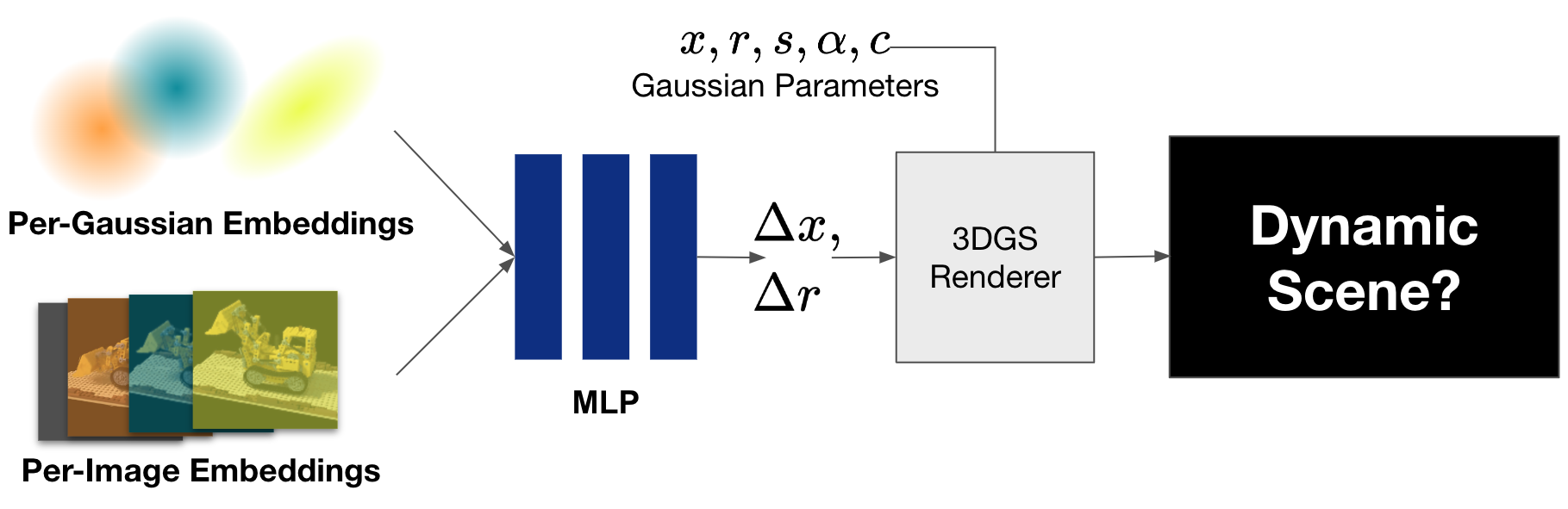
実験1
まずはシーンの動きをembeddingsとMLPで表現可能、という上記のアイデアを検証するため、CGで作成された人工的な画像データセットであるD-NeRF Dataset [Pumarola et al. 2020]を用いて実験を行いました。
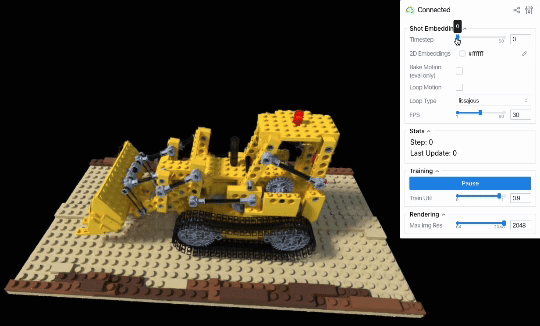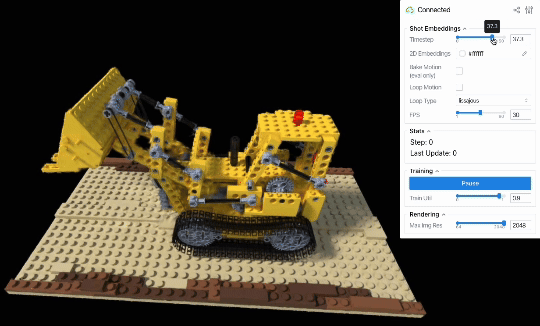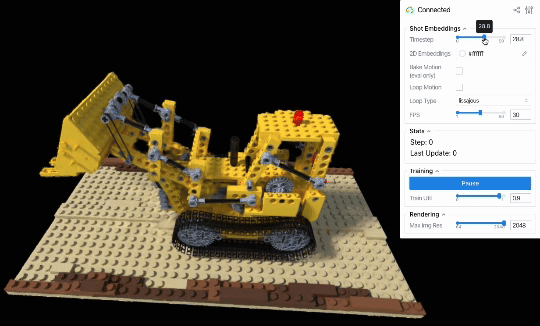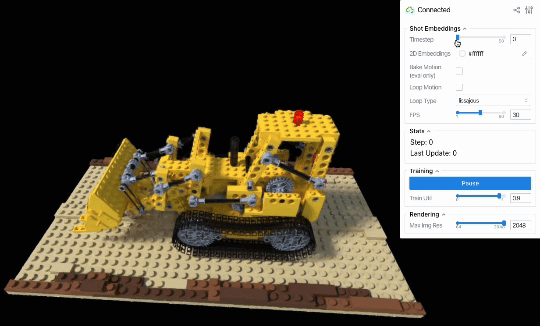
D-NeRFデータセットのLegoシーンには、レゴで作られたブルドーザーのブレードが上下する様子が、さまざまな角度から撮影された計50枚の連番画像として記録されています。撮影間隔は密で、かつ撮影順序や撮影時刻はデータセット中に明示されているため、動きを再構成するための十分な情報を含んだデータセット(すなわち、in-the-wildのデータと比較してより理想的なデータ)と言えます。
もしembeddingsとMLPが画像ごとのブレードの位置・回転変化量を上手く学習できていれば、連番画像に対応するembeddingsを順繰りに読み出すことで動きも再現できるはずです。
以下に結果を示します。
定量評価[3]
| PSNR↑ | SSIM↑ | LPIPS↓ | |
| Ours | 26.77 | 0.9000 | 0.0571 |
| 3DGS | 23.06 | 0.9290 | 0.0642 |
| 4DGS | 25.05 | 0.9376 | 0.0437 |
定性評価
定量評価からは、復元精度を表す3種の指標(PSNR, SSIM, LPIPS)について、通常の3DGSや連続情報を用いる4D再構成手法(4D Gaussian Splatting [Wu et al. 2023])と比較しても悪くない精度で復元を行えていることが分かります。
定性評価からも、学習した画像ごとのembeddingsを順に読み出すことでシーンの動きを再現できていることを見て取れます(ビューワー右上のシークバーは、何枚目の画像のembeddingsを読み出しているかを表しています)。
したがって、少なくとも画像の撮影順序が既知かつ撮影間隔が十分に短いという条件のもとでは、素朴にembeddingsとMLPの学習を行ったあとに撮影順序どおりにembeddingsを読み出せば、元の動きを再現するような動画をレンダリングできると分かりました。
本手法と似たアプローチを提案している関連研究としてE-D3DGS [Bae et al. 2024]がありますが、こちらでも時刻の連続情報を使って訓練を行うことで、embeddingsによる4D再構成が可能と報告されています。
実験2
続いて提案する再構成手法をin-the-wildの実画像に対しても適用してみます。 実験に用いたin-the-wildの実画像はメンターに撮影して頂いた自前のデータで、草木や花が風に揺れる様子が、さまざまな角度から撮影された30~40枚の画像として記録されています。
CGデータと比較して撮影間隔がスパースかつ不規則でで、連続的な時間情報を活用できないことが特徴です(すなわち、時刻のスカラー変数を用いるような既存手法を適用できません)。
以下に結果を示します。
画像ごとの定量評価[4]
| PSNR↑ | SSIM↑ | LPIPS↓ | |
| Ours | 22.18 | 0.701 | 0.200 |
| 3DGS | 21.99 | 0.697 | 0.206 |
(薔薇のシーン)
画像ごとの定性評価


画像ごとの定量評価・定性評価からは、通常の3DGSではブラーが発生するような風に揺れる花弁や葉も、鮮明に復元できていることを見て取れます。したがって、提案手法は時間情報を用いなくても各画像の変化にフィッティングできることが示されました。 この時点で、風が吹いているシーンを簡易的に撮影した場合でも精細に3D再構成できるという点で有用です。
動きの定性評価
さて、画像ごとの(すなわち特定の時刻に関する)再構成は上手くできましたが、動きのある再生についてはどうすべきでしょうか。 今回の設定ではそれぞれの画像の撮影間隔はスパースであり不規則であるため、風に揺れる花の位置がフレームごとに大きく変化しています。 そのため、たとえ画像の撮影順序がEXIF情報やファイル名で推測できたとしても、隣接する撮影画像同士でも動きが近いとは限りません。 たとえば、順番どおりに各画像のembeddingを使ってレンダリングすると、以下のように不自然な動きになってしまいます。

また、この不自然さは学習データによってはさらに大きくなることも予想されます。例えば上述のD-NeRFデータで学習した場合でも、訓練画像の順序が不明でランダムな状況では、各embeddingsを順に読み出しても当然動きは不自然になってしまいます。
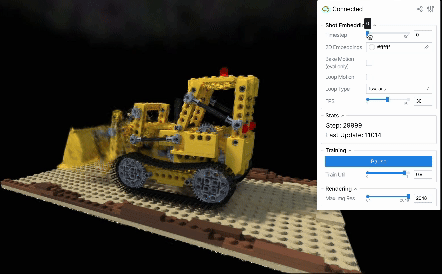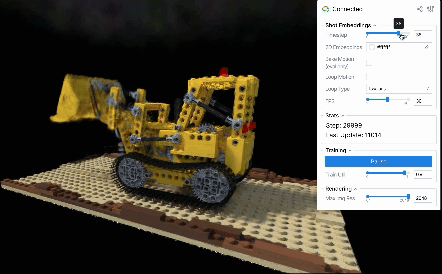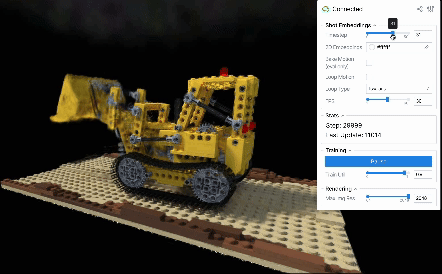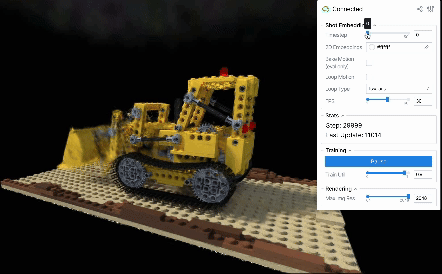
これらの結果から、in-the-wild画像においては、各画像のembeddingsを順に読み出す以外の方法で動きを生成する必要がありそうです。 どうすればin-the-wildな撮影画像での再構成結果を滑らかな動きで再生し、またそれをループさせられるでしょうか?
今回は、embeddings空間の特徴を利用した方法を導入しました。
embeddings空間の圧縮によるループ生成

学習後のembeddingsは高次元のベクトル表現として時間情報を持っていますが、その空間は疎であり解釈も難しいです。 そのため、画像ごとのembeddingsが暗黙的に保持する時間情報を主成分分析によって2次元に圧縮し、より密な2次元平面上でシーンの操作を行うアプローチを提案します。
これにより、動きの近いembeddingsは潜在空間上の近い位置に配置され、2次元平面上での連続的な変化がそのまま滑らかなシーンの動きを実現することが期待されます。 また、次元削減したことによって、訓練時には入力していないような補間的なembeddingsも適切な意味空間に乗りやすくなり、自然な動きが実現されやすくなることも考えられます。
したがって、圧縮後であれば、それに対応する2次元のUIを用いて連続的、かつ直感的にシーンの動きを編集して設定できるようになります[5]。
また圧縮後の2次元平面が解釈可能となるケースもあります。例えば、順序をシャッフルしたD-NeRFデータを再構成すると、圧縮後の2D embeddings平面上では各画像のembeddingsが概ね単調な時系列順に並びました。
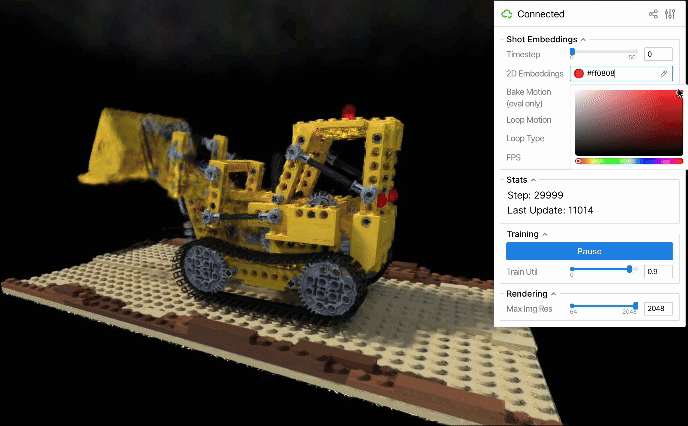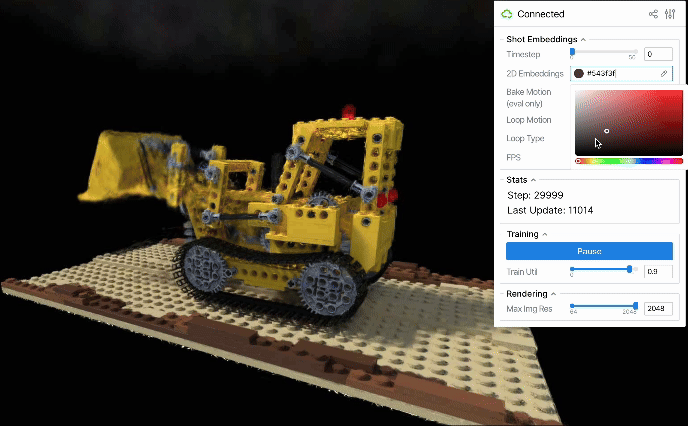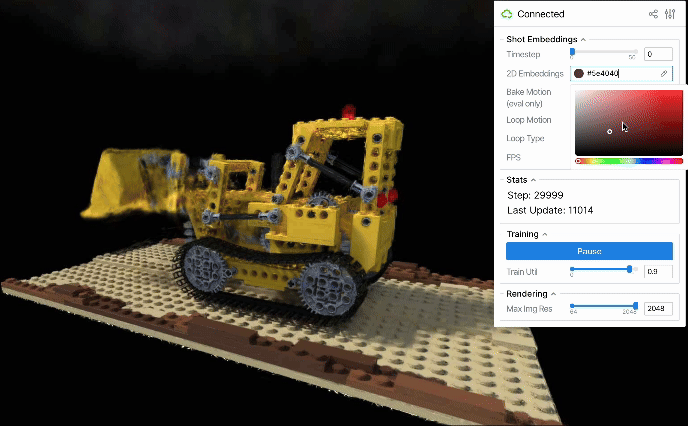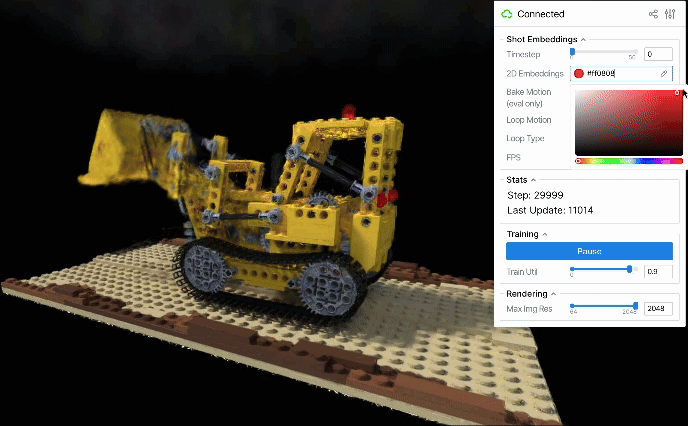
こうしたembeddings空間の圧縮は動きのループを生成するためにも有用と考えられます。2D embeddings平面上で閉じた軌道を設計すれば、それに応じたシーンの動きも途切れず連続的にループするはずです。
実験3
embeddingsの圧縮によって滑らかなループが生成されるかを検証するため、実験2と同じくin-the-wildの実データを用いて再構成を行いました。
2D embeddings平面上の軌道としては任意の閉じた軌道を用いることができますが、ここでは実装の容易さと適度な複雑さを両立するリサージュ曲線を採用しています。 各再生時刻ごとに軌道上の点を順番に取り、その2次元座標に対応するembeddingを使ったMLPの出力によって各ガウシアンを移動させてレンダリングを行います。
ループ出力
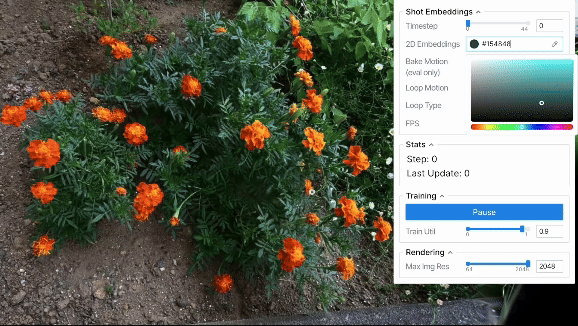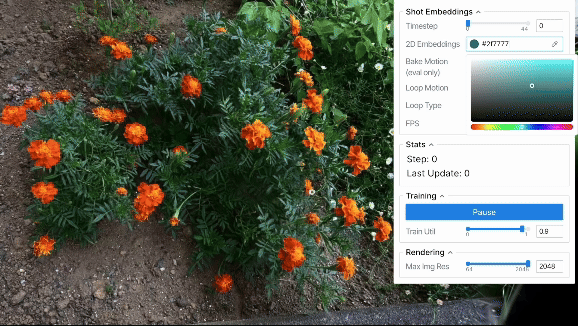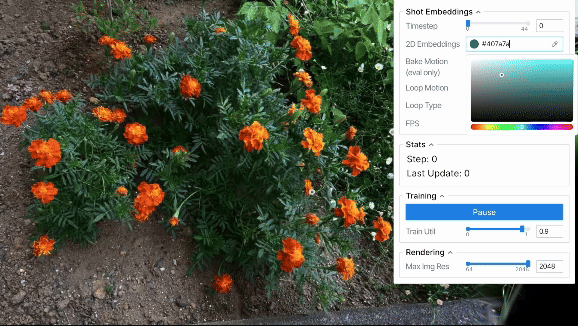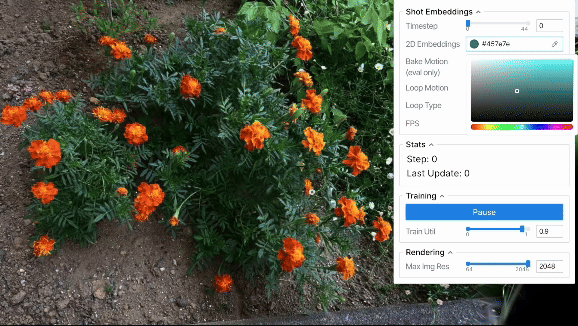
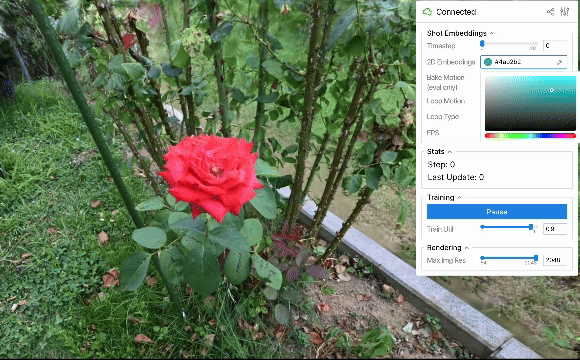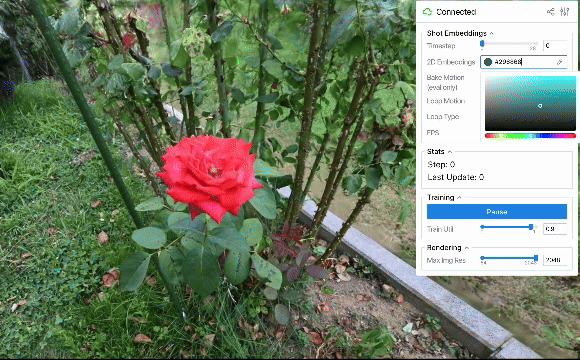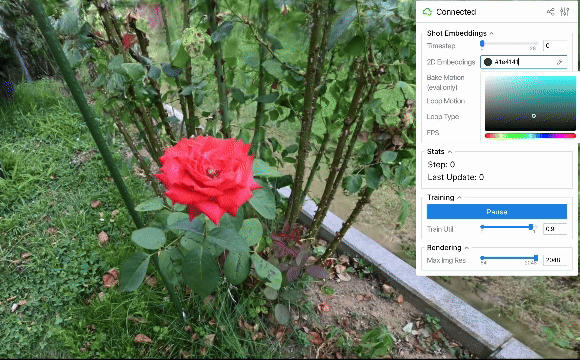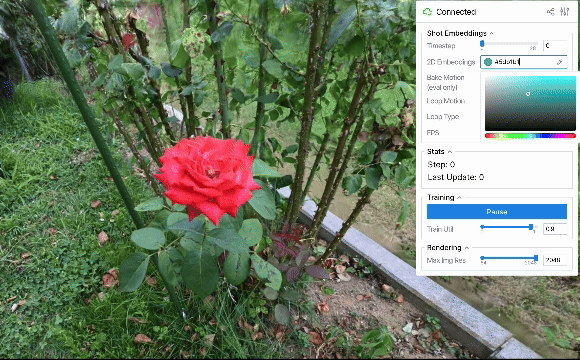
上に示した定性評価から、2D embeddings平面上で連続的な動きを作れば、それに応じてシーンを滑らかに動かせることが分かりました。 結果は省略しますが、軌道として単純な等速円運動などの様々なパターンを用いた場合も滑らかにシーンが動くことを確認できました。 また、ある程度のランダム性を持たせた軌道を設計すれば、より自然な風揺れを表現することも可能と考えられます。
MLP推論の省略によるレンダリング時の計算量削減
以上の手法でin-the-wild画像からループするシーンの4D再構成を行うことができました。
しかし、素朴な実装だとMLPの推論をガウシアンの個数分行う必要があり、レンダリング速度のボトルネックとなりえます。 したがって、リアルタイムレンダリングが望ましいバーチャルプロダクション背景への応用を考えると、高速化のために推論時の計算量を削減することも実用上重要です。 また、MLPに使う各ガウシアンごとのembeddingを保持しているため、モデルの保存容量やメモリ使用量の観点でもコストがかかっています。
今回はMLP計算を省略するために、以下に示す2通りの方法を提案します。
①Bilinear Interpolation
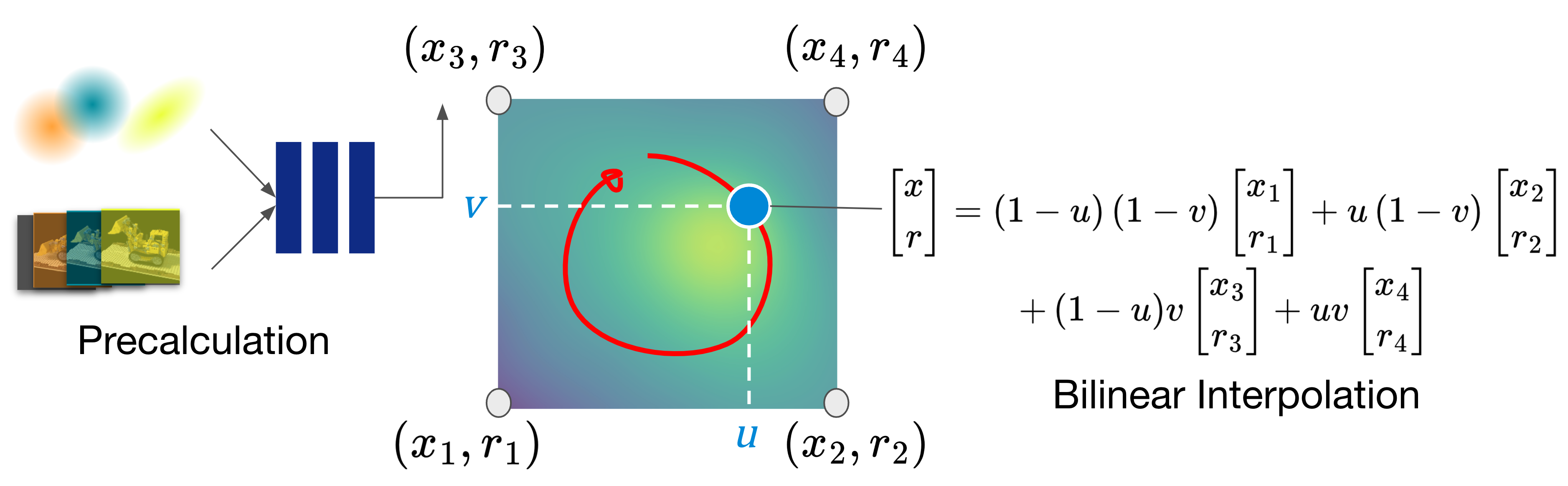
1つ目のアイデアは、事前計算したMLPの推論結果を2D平面上の数点に紐づけておき、シーンを操作する際にはそれらの計算結果をバイリニア補間するという方法です。推論結果を多く保存するほど正確な出力を得られますが、ここでは省メモリ化のため2×2のサイズを採用し、2D平面の四隅に計算結果を格納しています。各ガウシアンに対応する7次元のMLP出力(x, y, z, qx, qy, qz, qw)を4点分記録するため、必要なパラメータは28×N(N: ガウシアンの個数)となります。
②Linear Approximation
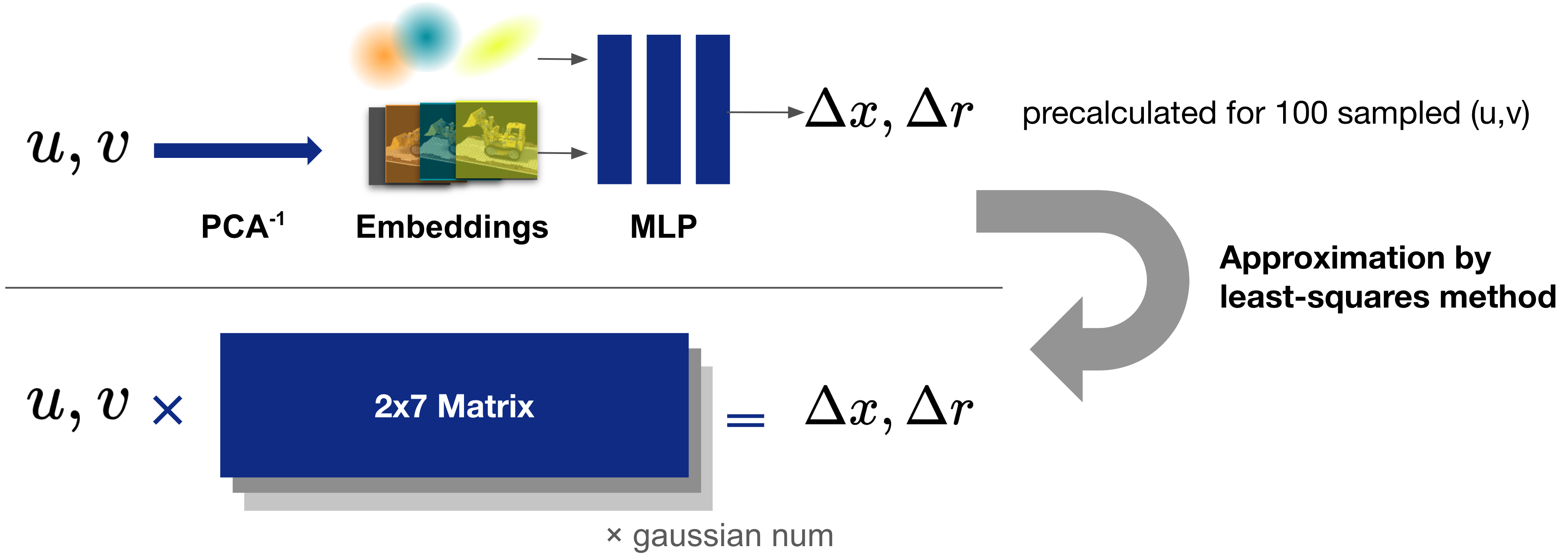
2つ目のアイデアは、ガウシアンごとにMLPの挙動を行列で線形近似するという方法です。2D平面上の座標(u, v)と、それをMLPに入力した時の出力(x, y, z, qx, qy, qz, qw)の対応関係を100点ほど事前計算しておき、それらの関係をできるだけ満たすような変換行列を最小二乗法により求めます。推論時にはガウシアンの個数分の2×7行列が分かっていれば良いため、14×Nと手法①より少ないパラメータでMLP計算を近似することができます。
実験4
上記の計算量削減手法の影響を検証するため、D-NeRFデータと実データに関してレンダリング時間とパラメータ、復元精度を計測しました。
D-NeRFデータ (合成データセット、240K gaussians)
| Rendering Time | Parameters | PSNR | SSIM | LPIPs | |
| Naive MLP | 0.00594 s | 7.2M | 28.69 | 0.9557 | 0.0258 |
| ①Bilinear Interp. | 0.00385 s | 6.7M | 25.56 | 0.9456 | 0.0399 |
| ②Linear Approx. | 0.00337 s | 3.4M | 26.02 | 0.9453 | 0.0393 |
in-the-wildデータ (実データセット、1M gaussians)
| Rendering Time | Parameters | PSNR | SSIM | LPIPs | |
| Naive MLP | 0.0294 s | 12M | 21.80 | 0.6649 | 0.1617 |
| ①Bilinear Interp. | 0.0114 s | 28M | 21.89 | 0.6654 | 0.1600 |
| ②Linear Approx. | 0.0114 s | 14M | 21.77 | 0.6629 | 0.1622 |
結果からは、①②いずれの手法についても素直にMLP計算した場合と比較してレンダリング時間を半分近くに抑えられていることが分かり、リアルタイムレンダリングを行うにあたって有用な工夫であることが示せました。
また合成データでの実験では補間・近似を行う①②の手法の復元精度がどちらも落ちているのに対し、実データでの実験では補間を行う①の手法が素直なMLP計算を精度で上回っています。 計算を省いているのに精度が向上するのは不思議な結果で、実データの孕む外部パラメータの誤差や画像の歪みなどが補間によって吸収されているのではないか、といった仮説が考えられますが、検証のためのさらなる実験はFuture Workとして残させて頂きます。
おわりに
総括すると、本インターンの成果は以下になります。
- 時間情報を持たないin-the-wildな画像から、4D再構成を行うことができた。
- 高次元のembeddingsを圧縮することで、滑らかで自然なループを生成できた。
- バイリニア補間やMLPの線形近似によって計算量を削減することができた。
本研究が4D再構成分野の発展に寄与すれば幸いです。実験に用いたコードとデータはこちらに公開しておりますので、良ければ何かに活用して頂ければと思います。
また、提案手法では草花の風揺れのような動きを上手く表現することができましたが、一方で踊る人間のような複雑な動きや水面の揺らぎのような細かい動きは上手く再構成できませんでした。より多様なシーンで再構成を行うためにはさらなる手法改善と実験が必要という展望を述べて、本稿の締めとさせて頂きます。
7週間という短い期間で分野のキャッチアップから有意義な研究成果を出すまでに至れたのは、ひとえに密なディスカッションと手厚いサポートをして頂いたメンターの松岡さん、小林さん、また加藤さんを始めとする3Dスキャンチームの皆さんのおかげです。改めて心よりの感謝を申し上げます。
ありがとうございました!
脚注
- フルタイトルは”Blowin’ in the Wild: Dynamic Looping Gaussians from Still Images”で、Bob Dylanの楽曲、Blowin’ in the Windのもじり。
- 動画ではなく画像を入力とする利点としては、ブラーのない高品質な教師画像を用いることができることも挙げられます。
- D-NeRFデータでは、10個の異なる時刻におけるnovel view画像の復元精度を平均することで定量評価を行っています。
- 単眼で撮影したin-the-wildデータでは、novel view画像は時刻不明になり評価が難しかったため、訓練用画像の復元精度によって定量評価を行っています。novel viewからの再構成の妥当性は定性的に確認しました。
- 初めから画像ごとのembeddingsを2次元として学習を行うことも可能ですが、学習結果が安定しないケースが多かったため、訓練後に主成分分析で2次元に圧縮する方法を採用しました。
Area