Blog
本記事は、2021年インターンシップで勤務した岩切秀規さんによる寄稿です。PFN は、深層学習を用いた物理探査技術の研究開発を三井物産株式会社との合弁会社 Mit-PFN Energy を通じて行なっており、本研究はその成果の一つです。これまでの取り組みは、過去のブログ記事でも取り上げていますのでご興味のある方はご覧ください。
はじめに
2021年夏季インターンシップに参加した、東京大学大学院修士2年の岩切秀規です。大学では数理情報第5研究室に属し、連続最適化の研究に取り組んでいます。
インターンシップでは「機械学習を用いた地震波解析」というテーマで開発に取り組み、そこでの成果を元に EAGE Annual Conference & Exhibition という国際会議で発表を行いました。
Hidenori Iwakiri, Naoto Mizuno, Takuya Shibayama, and Akira Kinoshita. Full-waveform inversion in optimization-friendly latent space created by a deep neural network. In EAGE Annual Conference & Exhibition, June 2022. https://doi.org/10.3997/2214-4609.202210381
本記事では、上記発表の内容についてご紹介します。
背景
地震波形逆解析
地震波形逆解析では、地震波の観測データから地下構造を推定する「逆問題」を解きます。反射法地震探査 (図1) では、地表面で人工的に地震波を発生させます。波は地層境界で反射し、地表面に戻ってくる一部の波を受振器によって観測することができます。観測データの振る舞いは波の伝播を支配する物理法則及び地下構造の特性によって決定されます。物理法則と地下構造の特性からどのような観測データが得られるかが決まる一方で、ここでは観測データから地下構造の特性を推定する問題を解くことを考えます。
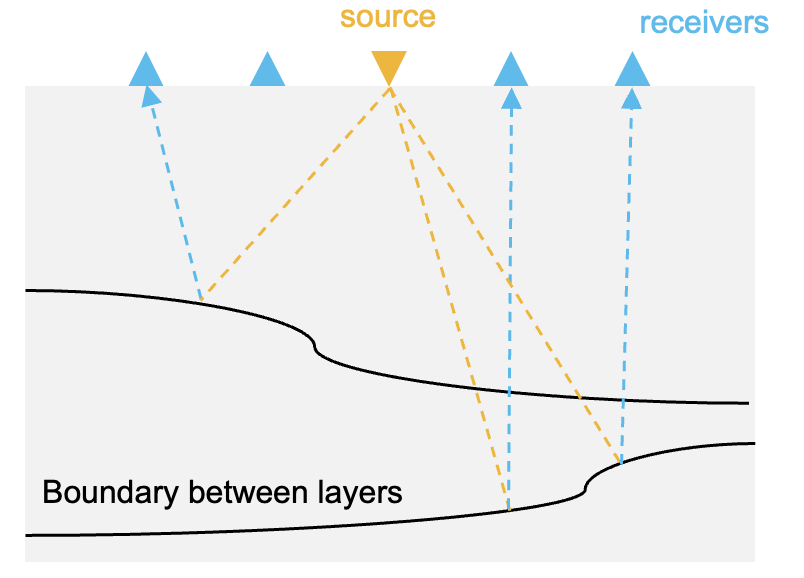
図1: 反射法地震探査におけるデータ取得の様子
図2: 地震波データ観測データは、図2に示すような2次元配列によって表現できます。縦軸が時間、横軸が水平位置に対応し、各成分が波の振幅を表します。これを地震波データと呼びます。また、地震波データの振る舞いを決定する地下構造特性として、P波の伝播速度を、図3に示すような2次元配列で表現します。縦軸が垂直位置、横軸が水平位置に対応し、各成分がP波速度を表します。これを速度構造と呼びます。本研究では、地震波データから速度構造を推定する問題を解くことを考えます。

図2: 地震波データ

図3: 速度構造
Full-Waveform Inversion (FWI)
FWI は、地震波形逆解析手法の一つであり、速度構造の最適化問題を解いています。誤差逆伝播法を用いる FWI (*1) のプロセスは以下のようになります (図4)。
- 初期値となる速度構造を与える。
- 速度構造上で微分可能な地震波シミュレーションを実行し、シミュレーション結果を得る。
- シミュレーション結果と地震波データとの差分を損失として計算する。
- 誤差逆伝播法を用いて損失の勾配を計算し、勾配法を用いて損失が小さくなるよう速度構造を更新する。
- 2〜4を適切な終了条件が満たされるまで繰り返す。
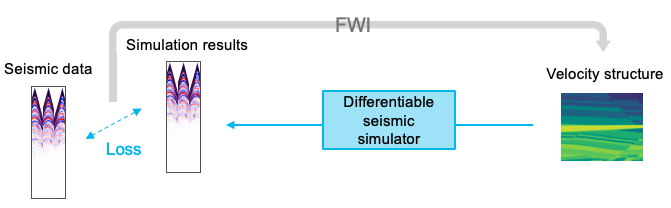
図4: 誤差逆伝播法を用いる FWI の概要
このように、FWI では、シミュレーション結果と地震波データ間の誤差が小さくなるように、速度構造を最適化しています。
真の速度構造は、シミュレーションを通して観測された地震波データを十分良く再現することが期待されます。そのため、最適化の結果、損失値が十分最適値に近くなれば、得られた解は「真の解」たる必要条件を満たすことになります。この意味で、推定結果に物理学的正当性を与えられることが FWI の長所として挙げられます。
一方で、FWI の最適化問題においてはしばしば、解が一つに定まらず、真の速度構造からかけ離れた悪質な最適解が多数存在します。そのため、損失値が十分最適値に近くなっても、得られた速度構造が真の速度構造に十分近いことまでは保証できません。それどころか、そのような悪質な解に陥ってしまうことで、FWI の推定精度は大幅に悪化してしまいます。
最適化問題における解の不定性を踏まえ、FWI の抱える2つの問題点を指摘することができます。
まず、このような不定性は、解のもつ自由度が高すぎることに起因しています。何の制約も課さない状態では、最適化対象となる速度構造には、画像のピクセル数分の自由度が与えられます。しかし、現実的な速度構造には、地層が鉛直方向に積み重なっている、深さが増すにつれて波の伝播速度が速くなる傾向にある、などといった制約があるため、実質的な自由度は遥かに小さいと考えられます。これらの制約を考慮しない状況下では、非現実的な速度構造を含んだ入力空間上で最適化を行うことになり、真の解に近い解が得られることは期待できません。
さらに、解の不定性によって、高い初期値依存性が生じてしまっています。FWI が解く速度構造の最適化問題においては、推定精度が大幅に悪化する悪質な最適解に陥るのを避けるため、正解に近い速度構造を初期値として設定する必要があります。初期構造の設計は通常、走時トモグラフィー等を用いて実施されますが、これらには、専門家による数ヶ月以上に渡っての解析が必要となります。そのため、FWI を実施する上での大きなボトルネックとなっていました。
上記で説明した FWI はあくまでもナイーブなものであり、FWI の精度向上や工数削減を目的として、これまで様々な研究がなされています [1, 2, 3] 。
また、地震波データから速度構造を推定する問題を2次元画像の変換問題と捉え、深層学習を適用する研究も近年行われています [4, 5] 。しかし、これらは地震波データと速度構造の関係性を帰納的にモデリングするため、FWI と異なり、得られた速度構造がシミュレーションを通じて地震波データを再現するとは限りません。そのため、シミュレーションによる再現性の確認が追加で必要となります。
提案手法
そこで我々は、FWI がもつ地震波シミュレーションによる物理学的正当性を満たしつつ、深層学習を用いて上記2つの問題を解決するため、図5に示すような手法を提案しました。
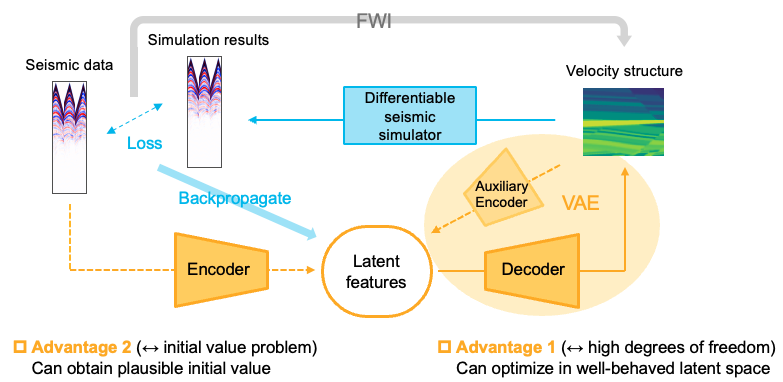
図5: 提案手法の概要
まず、解のもつ自由度を減らすために、「現実的な速度構造のみを表現する潜在空間」を深層生成モデルによって構築することを考えました。そしてさらに、速度構造の最適化に代わり、潜在変数の最適化を実施しました。潜在空間の次元数は、速度構造空間の次元数よりも遥かに小さく設定され、最適化が容易になることが期待されます。最適化が実行できれば、得られた潜在変数をデコーダーに通すことで、速度構造の推定結果を得ることができます。
深層生成モデルの選択にあたっては、学習の安定性の面から、Variational AutoEncoder (VAE) を使用することが適当だと考えました。そして VAE の中でも高い表現力を持つ Nouveau VAE (NVAE) [6] を採用しました。NVAE は階層的な潜在変数を用い、加えてアーキテクチャにも様々な工夫を施しています。これにより安定した学習のもと、広範囲にわたる関係性を精度良く捉えられることが期待されます。
NVAE は、現実的な速度構造を集めたデータセットを用いて学習できます。今回の実験では、PFN が以前作成した速度構造生成システム [5] (*2) を訓練データの生成に利用しました。
潜在変数の最適化にあたっては、損失の潜在変数についての勾配が必要になります。これは、NVAE のデコーダーが微分可能であることを利用し、速度構造についての勾配をデコーダーにて逆伝播させることで得ることができます。
続いて、初期値依存性の問題を解決するために、地震波データから潜在変数を推定するエンコーダーを構築することを考えました。速度構造と対応する地震波データは同じ物理学的特性を表現しており、それぞれが同一の潜在変数によって表現可能と仮定します。すると、NVAE を用いて実装した速度構造と潜在変数間の写像だけでなく、地震波データと潜在変数間の写像も考えることができます。これを踏まえ、地震波データから潜在変数への写像であるエンコーダーをニューラルネットワークを用いて実装しました。エンコーダーの推定精度が十分高ければ、地震波データだけから、対応する速度構造を表現する潜在変数を推定することができます。推定された潜在変数は、最適化にあたっての良い初期値になっていることが期待されます。
エンコーダーの学習にあたっては地震波データと、対応する潜在変数が必要になります。これらエンコーダーの入出力は共に、同一の速度構造と対応します。地震波データは、速度構造上でシミュレーションを走らせることで取得できます。対応する潜在変数に関しても、学習済の NVAE の Auxiliary Encoder (図5参照、潜在変数を推定するエンコーダーとは異なることに注意) に速度構造を渡してあげることで、取得できます。
提案手法では FWI と同じく、地震波シミュレーションによる物理学的正当性が担保されます。すなわち、損失が十分小さくなれば、最適化された潜在変数に対応する速度構造が地震波データをシミュレーションによって十分よく再現します。
実験
設定
実験に用いた速度構造は、前述したPFNの速度構造生成システムによってパラメトリックに生成された Parametrically Generated (PG) モデル、及びベンチマークでよく用いられる Marmousi モデル [7] の2種類から成ります。前者の生成過程を決定づけるパラメータの設定にあたっては、Marmousi モデルの地質学的情報 (地震波速度の大凡の範囲など、現実の解析で使用可能と想定される大まかな情報に限る) を用いています。NVAE 及びエンコーダーの訓練には、それぞれ8万個、5万個の PG モデルを使用しました。推論には、学習に用いられていない PG モデル200個と、Marmousi モデル100個を使用しました。
また、以下の3つの手法を比較対象としました:
- Naive FWI
- 最適化方法: 速度構造を直接最適化 (図4)
- 初期値: Uniform (全成分を正解の平均値に設定した速度構造)
- 提案手法 (Uniform)
- 最適化方法: 潜在変数を最適化 (図5)
- 初期値: Uniform (全成分を正解の平均値に設定した速度構造に対応する潜在変数)
- 提案手法 (Encoder Output)
- 最適化方法: 潜在変数を最適化 (図5)
- 初期値: EncoderOutput (エンコーダーによって推定された潜在変数)
Naive FWI と提案手法 (Uniform) を比較することで、解のもつ自由度を低く抑えたことによる効果を、提案手法 (Uniform) と 提案手法 (Encoder Output) を比較することで、エンコーダーによる初期値推定の効果を測ることが狙いです。
これら3手法の実装にあたっては、微分可能なシミュレーターを (必要に応じて) 深層学習モジュールと組み合わせた上で、順伝播及び逆伝播を実行する必要があります。本研究では、シミュレーターとして Deepwave と呼ばれる PyTorch で実装されたモジュールを用いることで、エンドツーエンドにこれらの計算を行っています。
結果・考察
まず図6に、PG モデルに対する推論結果を示します。速度構造に制約が課されていない Naive FWI では、深部での速度が遅い「速度構造らしくない」解が出力されています (c) 。一方、提案手法 (Uniform) では、同じ一様初期値を用いているのにも関わらず、遥かに高い精度で速度構造を推定できています (d) 。さらに (b) で示したエンコーダーによって推定された初期構造を用いることで、提案手法 (Encoder Output) の精度は更に向上し、深部の断層を捉えることに成功しています (e) 。
経験的に Naive FWI では、推定精度の良し悪しに関わらず損失が最適値付近まで下がってしまうことを確認しています。一方、提案手法では、推定精度が低いと、損失値が下がり切らないことが確認されています。この観察は、提案手法において損失値を確認することで、推定結果の妥当性を評価できる可能性を示唆しています。

図6: PG モデルに対する推論結果 (*3)
次に図7に、Marmousi モデルに対して提案手法 (Encoder Output) を適用した結果を示します。エンコーダーによって推定された初期構造 (b) は、地層境界や速度の推定が不正確ではあるものの、深さが増すにつれて速度が速くなるという大まかな傾向を捉えられています。提案手法 (Encoder Output) によって得られた速度構造 (e) は、深さ 4 km より下側に位置する、不整合面下の斜めに連なっている地層を捉えられていないものの、深さ 0~3.5 km における地層境界及び速度を高い精度で推定できています。
また、別の観察により、 Marmousi モデルに含まれる速度構造を、今回の推定結果より正確に表現するような潜在変数の存在を確認できています。そのため、エンコーダーによる初期値推定の精度を上げることが、更なる精度向上に向け重要だと考えられます。
NVAE やエンコーダーの訓練には Marmousi モデルの地質学的情報しか用いていません。そのためこの結果は、未知の速度構造を、現実的に使用可能と思われる情報だけを用いて、高精度で推定できる可能性を示唆しています。一方で、より複雑な速度構造の推定や地震波データにノイズが含まれる状況での推定に対し、本手法の性能を評価することは今後の課題となります。
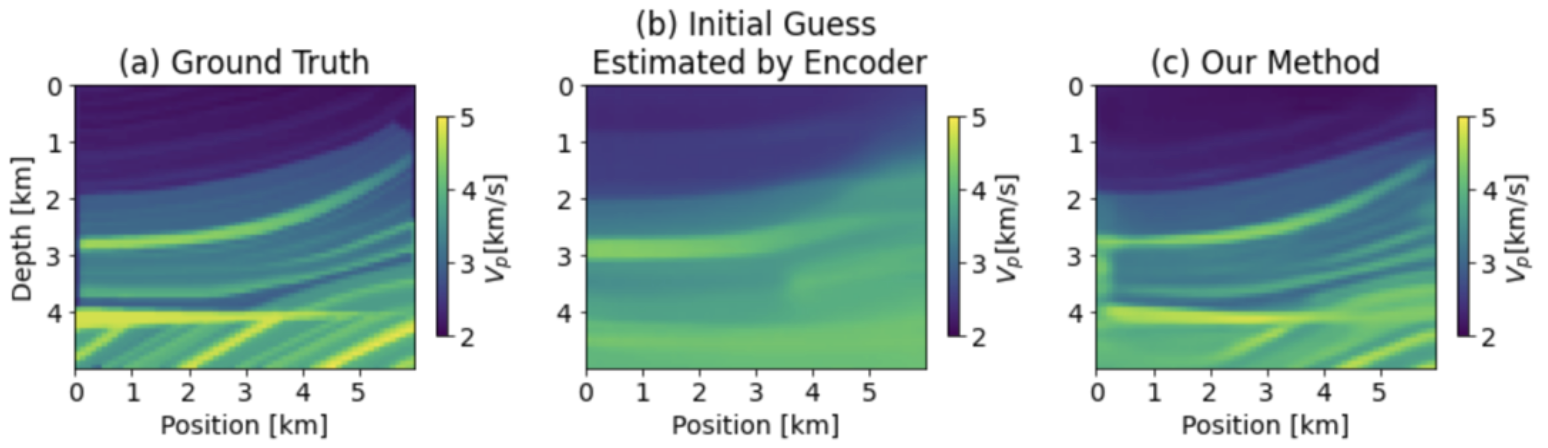
図7: Marmousi モデルに対する提案手法の推論結果 (*3)
まとめ・謝辞
本研究では、地震波形逆解析において用いられ、速度構造の最適化問題を解く FWI の抱える (1) 解に高すぎる自由度がある、(2) 初期値への依存性が高い、という2つの問題点に対し、FWI と深層学習を組み合わせることで解決を試みました。具体的には、 (1) 現実的な速度構造を表現する潜在空間を NVAE によって構築し、速度構造空間より次元の低い潜在空間上で最適化を実施する、(2) 地震波データから良い初期値を推定するエンコーダーを構築する、という2つのアプローチを実装しました。実験において、これら2つのアプローチの有効性も確認しました。
大学の研究分野とは全く異なるドメインの問題に取り組み、苦労することも多くありましたが、短いインターンシップ期間の中で成果を上げることができ、国際学会で発表できたことを非常に嬉しく思います。充実した日々を過ごし、満足のいく成果を出すことができたのは、ひとえにPFN 社員の皆さんのサポートによるものです。特に、地震波解析チームの柴山さん、水野さん、木下さん、日暮さんからは、 研究・開発・執筆、全てにおいて様々なアドバイスをいただき、大変お世話になりました。この場を借りてお礼申し上げます。ありがとうございました。
*1: 一般に、FWI は損失の勾配の計算に誤差逆伝播法を用いるとは限らず、シミュレーターが微分可能であることも仮定しません。
*2 この地下構造生成システムは微分可能でないため、速度構造空間よりも低次元な最適化空間を構築する目的で、NVAE の代わりに用いることはできません。
*3: 今回の EAGE Annual Conference & Exhibition における発表からの引用です。
参考文献
[1] Z. Zhang and L. Huang. Double-difference elastic-waveform inversion with prior information for time-lapse monitoring. Geophysics, 78(6): 259-273, 2013.
[2] K. Tran, M. McVay, M. Faraone and D. Horhota. Sinkhole detection using 2D full seismic waveform tomography. Geophysics, 78(5): 175-183, 2013.
[3] A. Guitton. Blocky regularization schemes for full waveform inversion. Geophysical Prospecting, 60(5): 870-884, 2012.
[4] M. Araya-Polo, J. Jennings, A. Adler and T. Dahlke. Deep-learning tomography. The Leading Edge, 37(1): 58-66, 2018.
[5] T. Shibayama, N. Mizuno, H. Kusano, A. Kinoshita, M. Minegishi, R. Sakamoto, K. Hasegawa and F. Kachi. Practical deep learning inversion using neural architecture search and a flexible training dataset generator. In EAGE Annual Conference & Exhibition, 2021.
[6] A. Vahdat and J. Kautz. NVAE: A deep hierarchical variational autoencoder. In Advances in Neural Information Processing Systems, pages 19667-19679, 2020.
[7] G. S. Martin, R. Wiley and K. J. Marfurt. Marmousi2: An elastic upgrade for Marmousi. The Leading Edge, 25(2): 156-166, 2006.




