Neural Network Potentialを用いたタンパク-薬剤結合自由エネルギー計算の改善

Area

Bioinformatics / Healthcare

Chemoinformatics / Materials Science

Tag

# Drug discovery

Mizuki Takemoto

Researcher

本記事は、2020年インターンシップで勤務した富田篤弘さんによる寄稿です。

はじめに

PFN2020夏季インターンに参加させていただいた、東京大学博士2年の富田篤弘です。研究室では、クライオ電子顕微鏡を用いたタンパク質の単粒子構造解析と立体構造を用いた分子動力学 (MD) シミュレーションの研究を行なっています。今回のインターンではMDシミュレーションと機械学習を組み合わせてタンパク質と薬剤の結合の強さを高精度に予測する研究に取り組みました。今回の記事では、取り組んだ課題に関連した論文[1] “Towards chemical accuracy for alchemical free energy calculations with hybrid physics-based machine learning / molecular mechanics potentials” について紹介したいと思います。

背景: 創薬における自由エネルギー計算の利用

創薬現場では、数十万～数百万の化合物群の中から膨大なセレクション実験を行い、薬の候補となるHit化合物の探索が行われています。そのような膨大な実験に伴う試薬代・人件費・時間的コストなどを軽減するために、コンピューターを利用して薬の候補を絞り込むインシリコスクリーニングと呼ばれる手法が利用されています。また、得られたHit化合物をより強い結合強度、より良い薬物動態をもつ化合物に変換していくリード最適化と呼ばれる工程もあり、ここでも提案化合物の合成や実験にかかる費用の軽減も課題になっています。結合自由エネルギーの予測は、そのようなインシリコスクリーニングやリード最適化の中で広く用いられている手法の一つです。薬の標的となるタンパク質に対して候補化合物の結合自由エネルギーを予測することで、強い結合エネルギーを持つ化合物を薬の候補として絞り込みます。

現在、精緻な結合自由エネルギーの予測には分子動力学 (MD) シミュレーションを用いた手法が主に用いられています。しかしながら、MDシミュレーションに用いる古典力場は計算量を減らすために自由エネルギーに寄与する多くの項を省略しているため、結合自由エネルギーの計算には、うまく計算が収束するような場合であっても1-2 kcal/mol程度の誤差がありました。

結合自由エネルギー計算とは何か

下記のようなタンパク質 (P) とリガンド (L) が結合し複合体 (PL) を形成する反応を考える際、

\[ \mathrm{P} + \mathrm{L} \rightleftharpoons \mathrm{PL} \tag{1} \]

反応物 (タンパク質単体Pとリガンド単体L) の自由エネルギーと、生成物 (リガンド-タンパク質複合体PL) の自由エネルギーの差を結合自由エネルギー (\(\Delta G\)) と呼びます。熱力学の教えるところによれば、\(\Delta G\)は結合の際のエンタルピー変化 (\(\Delta H\)) とエントロピー変化 (\(\Delta S\)) 等を用いて、

\[ \Delta G = \Delta H – T \Delta S \tag{2} \]

と表せますが、一方で \(\Delta G\) は、結合の強さを表す指標である解離定数 \(K_d\)と以下のような関係があるため、\(\Delta G\)を通してタンパク質とリガンドの結合の強さを知ることができます。

\[
\frac{[\mathrm{P}][\mathrm{L}]}{[\mathrm{PL}]} = K_d \\
\Delta G = k_B T \log K_d \tag{3} \]

そのため、創薬ではより\(\Delta G\)が大きい化合物をデザインすることが重要となってきますが、
もしこの\(\Delta G\)を計算機シミュレーションで予測することができれば、実験することなく薬剤候補を絞り込むことが可能となり、より効率的な創薬を行うことができます。\(\Delta G\)の予測方法としては、高速ながらも精度が劣るドッキングシミュレーションや、計算量が多いがより高精度な予測が可能なMDシミュレーションを用いた方法等があります。通常、自由エネルギー計算という場合、後者のMDシミュレーションを用いた方法を指しますが、MDシミュレーションに基づいた方法には、さらに、自由エネルギー摂動 (FEP) 法や熱力学的積分法 (TI) 法などがあります (詳しくはこちらの文献[2] 等を参照してください) 。

結合自由エネルギー計算の問題点

この\(\Delta G\)を予測するための自由エネルギー計算ですが、依然実験値に対して予測値が大きく外れるケースがあることが知られています。原因としては大きく2点挙げられます。
一点目の問題点は、MDシミュレーションに用いる力場の不正確性によるものです。MDシミュレーションは古典力学に基づくため、本来は量子力学で扱うべき原子間の相互作用を、古典の運動方程式で扱えるように近似した以下のような式(4) (古典力場) を用います。以下に良く用いられる例をあげました。

\[ E_{pair} = \sum_{bonds} K_r (r – r_{eq})^2 + \sum_{angles} K_{\theta} (\theta – \theta_{eq})^2 \\
+ \sum_{dihedrals} \frac{V_n}{2} \left[ 1 + \cos (n\phi – \gamma) \right] \\
+ \sum_{i<j} \left[ \frac{A_{ij}}{R_{ij}^{12}} – \frac{B_{ij}}{R_{ij}^6} + \frac{q_i q_j}{\epsilon R_{ij}} \right] \tag{4} \]

AMBER力場の計算式: 1項目は結合距離・2項目は結合角・3項目は二面角・4項目はLennard-Jonesポテンシャル及び静電相互作用を計算している。 (http://ambermd.org/antechamber/gaff.htmlより)

この式(4)の\(K_r\)や\(r_{eq}\)等は、MDシミュレーションの結果が実験値を再現するように経験的に決める必要があるパラメータ (力場パラメータ) です。タンパク質を構成する20種の天然アミノ酸の原子等については、ここ数十年かけて、実験値を再現する力場パラメータが精力的に研究され、決定されてきました。一方で薬剤や阻害剤を構成する原子の力場パラメータについては、原子が置かれる環境が化合物によって大きく異なる等の理由から、化合物毎に適切なパラメータを自前で決定する必要があります。ある程度自動化する方法も提唱されてきましたが、タンパク質側に比べてどうしても精度が劣ってしまうというという問題があり、特に二面角のポテンシャルは正確に決定するのが難しいことがよく知られていました。この精度低下は、式(2)の\(\Delta H\)項の不正確性に帰結します。

二点目の問題点は、MDシミュレーションによるサンプリングが不十分であるケースがあることがあげられます。タンパク質の種類によってはリガンドや化合物の結合に伴って大きな構造変化が起こるものがあります。そのような場合、MDシミュレーションで計算可能な時間内に十分な構造サンプリングを行うことができず、特に式(2)のうち、エントロピーが関与する\(-T \Delta S\)の項の精度が低下するなどして、計算結果が不正確になることが知られています。

本論文での方法

今回紹介する手法では一点目の問題点について、ニューラルネットワークポテンシャル(Neural Network Potential; NNP)を用いた解決を試みています。NNPは量子化学計算の結果得られる原子間相互作用を再現するよう学習させたニューラルネットワークであり、各原子の座標を受け取ることでエネルギーと力の近似値を返します。NNPの推論計算は量子化学計算に比べて計算量が非常に少ないため、より大きな系のシミュレーションを長時間行うことが可能です。

このように、従来の量子化学計算に比べて少ない計算量を実現しているNNPですが、古典力場だけを用いたMDシミュレーションに比べると、依然、計算量は増大するため、タンパク質・薬剤複合体等の数万原子を含む大きな系に直接応用することは困難です。そこで、今回紹介する手法では、リガンド内部の相互作用計算のみにNNP (以下MLとも表記) を適用して、長距離相互作用やタンパク-リガンド相互作用、水との相互作用は従来の古典力場 (MM) で計算することで、NNPを用いた精度改善を試みています (図1) 。つまり、MMで計算した系全体のポテンシャルから、MMで計算したリガンドのみのポテンシャルを差し引き、代わりにNNPで計算したポテンシャルを足して全体のポテンシャルエネルギーとしています。筆者らはこれをML/MMポテンシャルと呼んでいます。本論文ではNNPとしてANI-2x[3]を用いています。

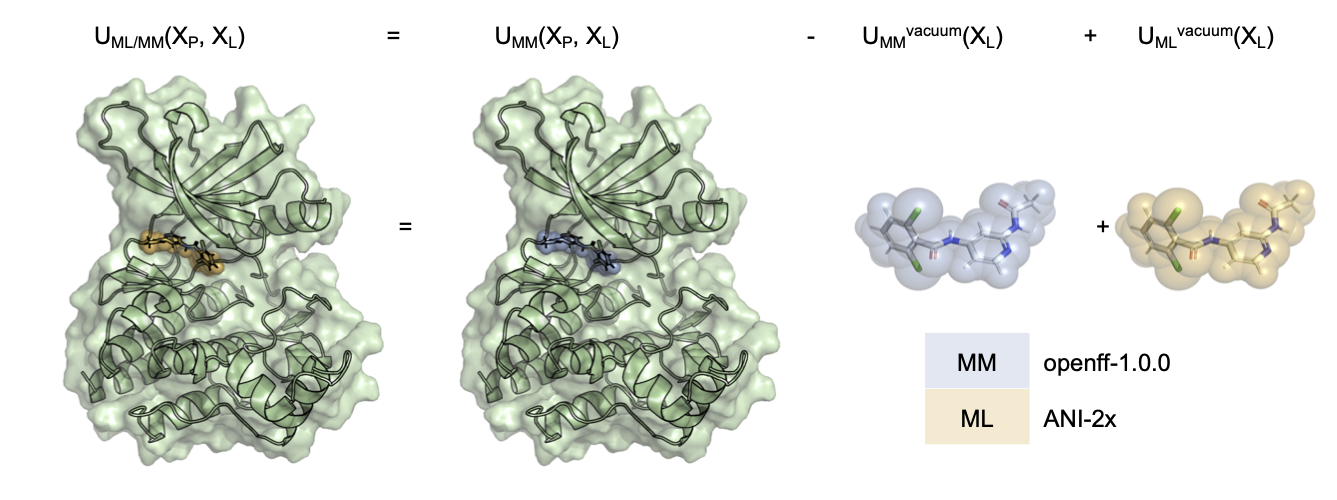
図1: ML/MMポテンシャルの構築。古典力場にはopenff-1.0.0を使用し、NNPにはANI-2x[3]を使用している。 (論文[1] Fig. 1より)

しかしながらこのML/MMポテンシャルを用いても、十分な精度の自由エネルギー計算 (累計数十ナノ秒程度が必要) を行うには、依然として長大な計算時間を要します。そこで筆者らは、MMでの計算結果をML/MMポテンシャルの計算で補正する手法を取っています。具体的には、一度古典力場で通常の自由エネルギー計算で行われる通りにL1とL2の結合自由エネルギーの差 (図2、①\(\Delta \Delta G_{MM}\) ) を計算します。次に、リガンド部分を古典力場からML/MMポテンシャルに変化させたときのエネルギー差を求めるために、非平衡状態 (NEQ) を利用した自由エネルギー計算を用いています。ここでは短時間(~10 ps)のシミュレーションを何回か行い、その自由エネルギー変化 (図2、②,③) を記録しておきます。①と②③を組み合わせることで、ML/MMポテンシャル下でのリガンドL1とL2の結合自由エネルギー差 (図2： \(\Delta \Delta G_{ML/MM}\) ) を計算しています。

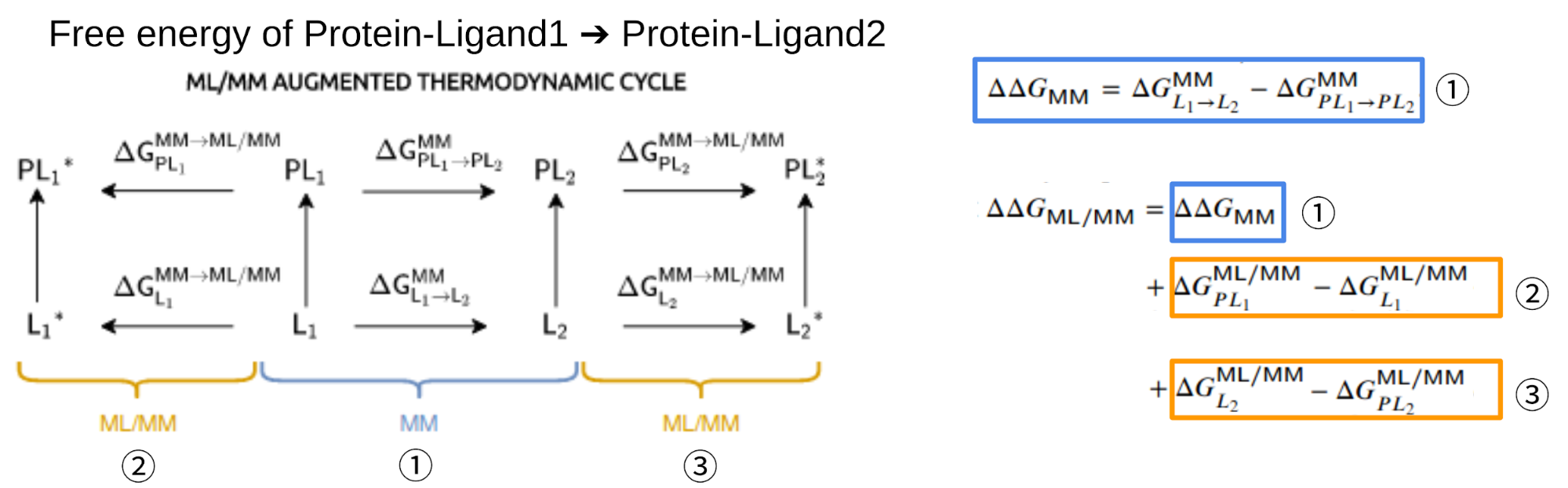
図2: 本手法で用いる熱力学サイクル (左)。各サイクルを1周すると状態が元に戻る ( \(\Delta G\) が0になる) ことを利用して右①式や \(\Delta \Delta G_{ML/MM}\) の値を求めることができる。 (論文[1] Fig. 3より改変)

実際の系へ適用した結果

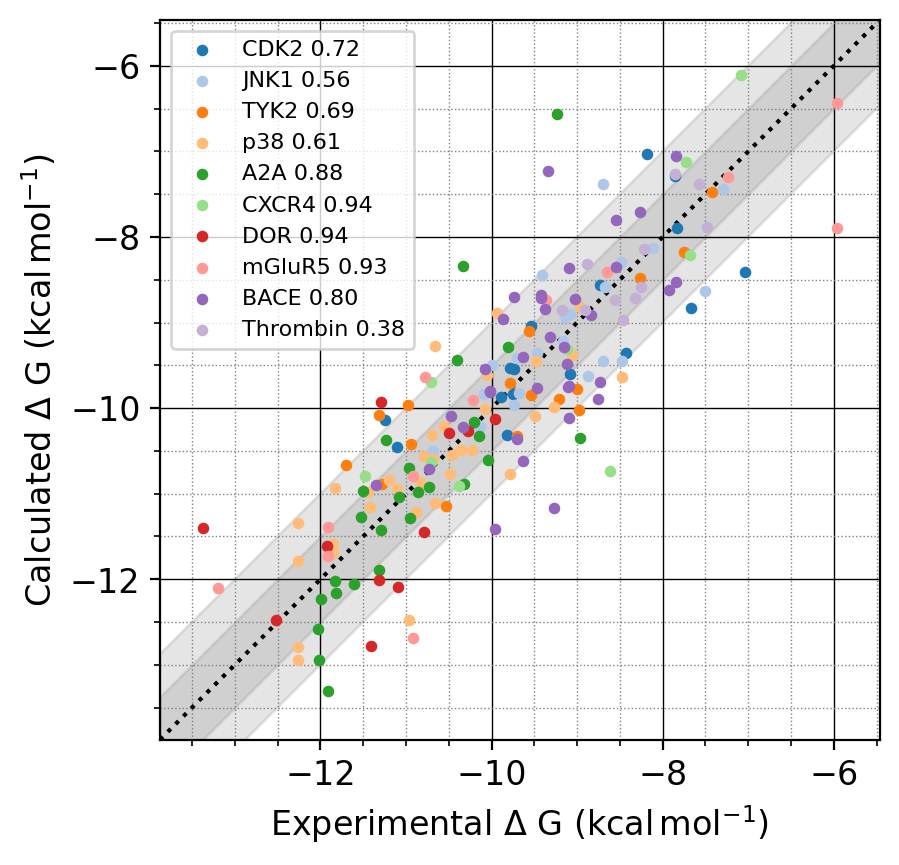
本論文では、チロシンキナーゼ2 (図3 Tyk2; PDBID 4GIH) に対する阻害剤のベンチマークセット(Schrödinger JACS benchmark set [4])を用いて、古典力場のみを用いたケースとNNPを併用したケースでΔGの実験値との比較を行っています (図3) 。

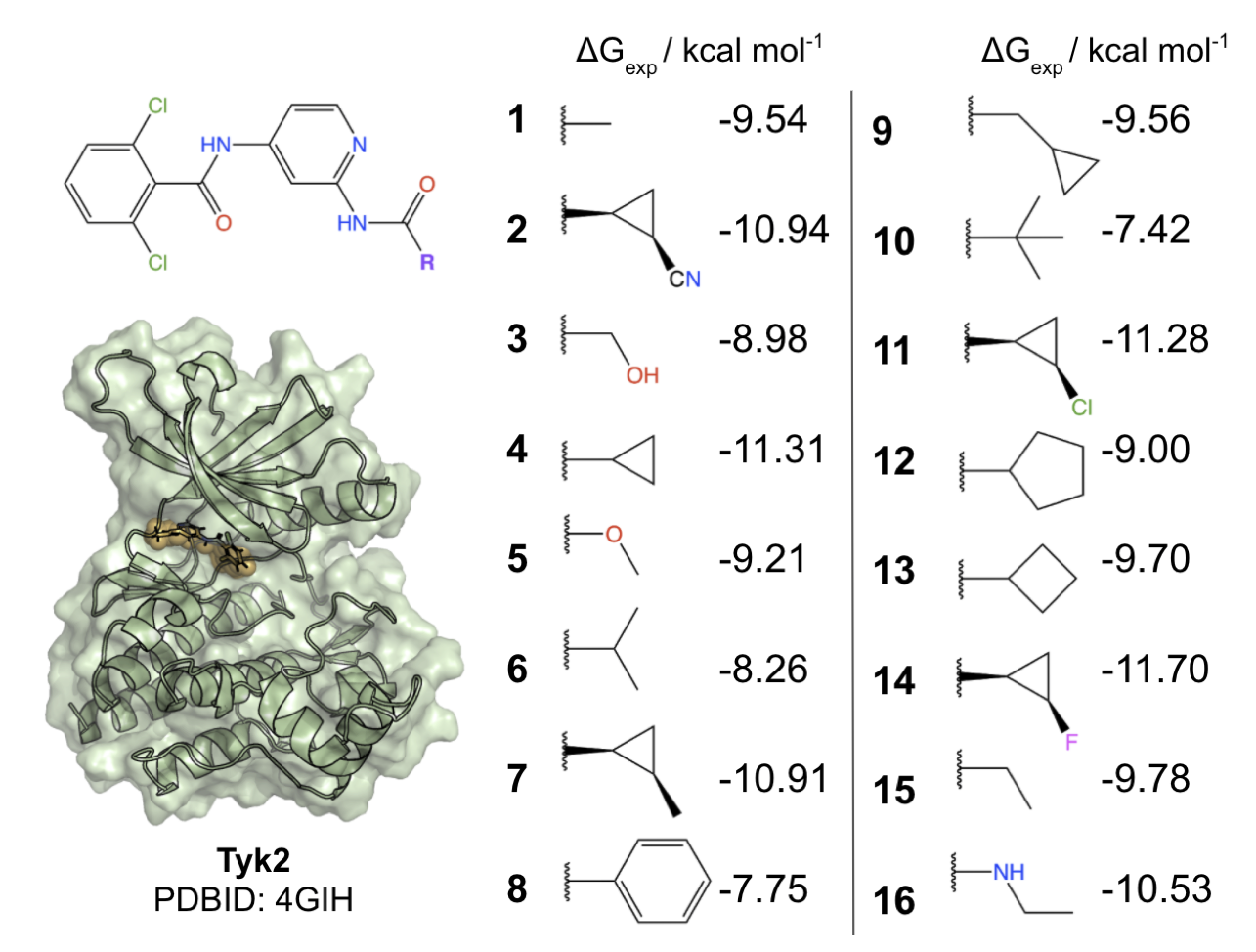
図3: 論文で使用しているTyk2の構造と、阻害剤の構造および実験値。論文[1] Fig. 2より

古典力場では \(\Delta G\) のRMSEが0.97 kcal/mol程度であった一方で、MM/MLでは\(\Delta G\)のRMSEが0.47 kcal/mol程度になり、精度の向上に成功しました (図4、5) 。 (なお、この論文では複数の結合自由エネルギーの差\(\Delta \Delta G\)から\(\Delta G\)をもとめるのにこの論文[5]の方法を使っています。)

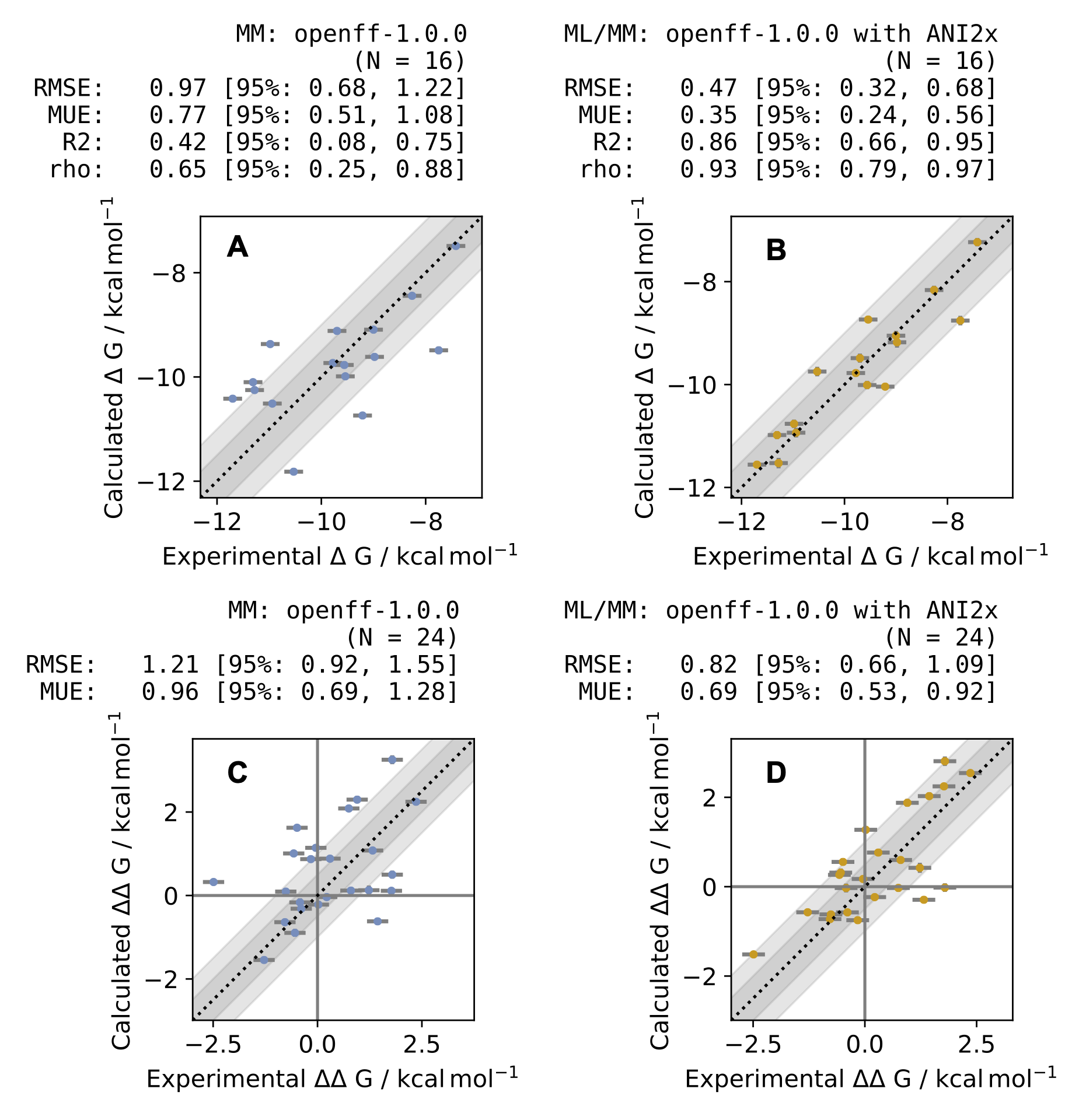
図4: ML/MMポテンシャルによる補正の効果。MMのみの結果 (左) よりも、ML/MMを取り入れる方 (右) が実験値との相関が改善されている。論文[1] Fig. 6より。

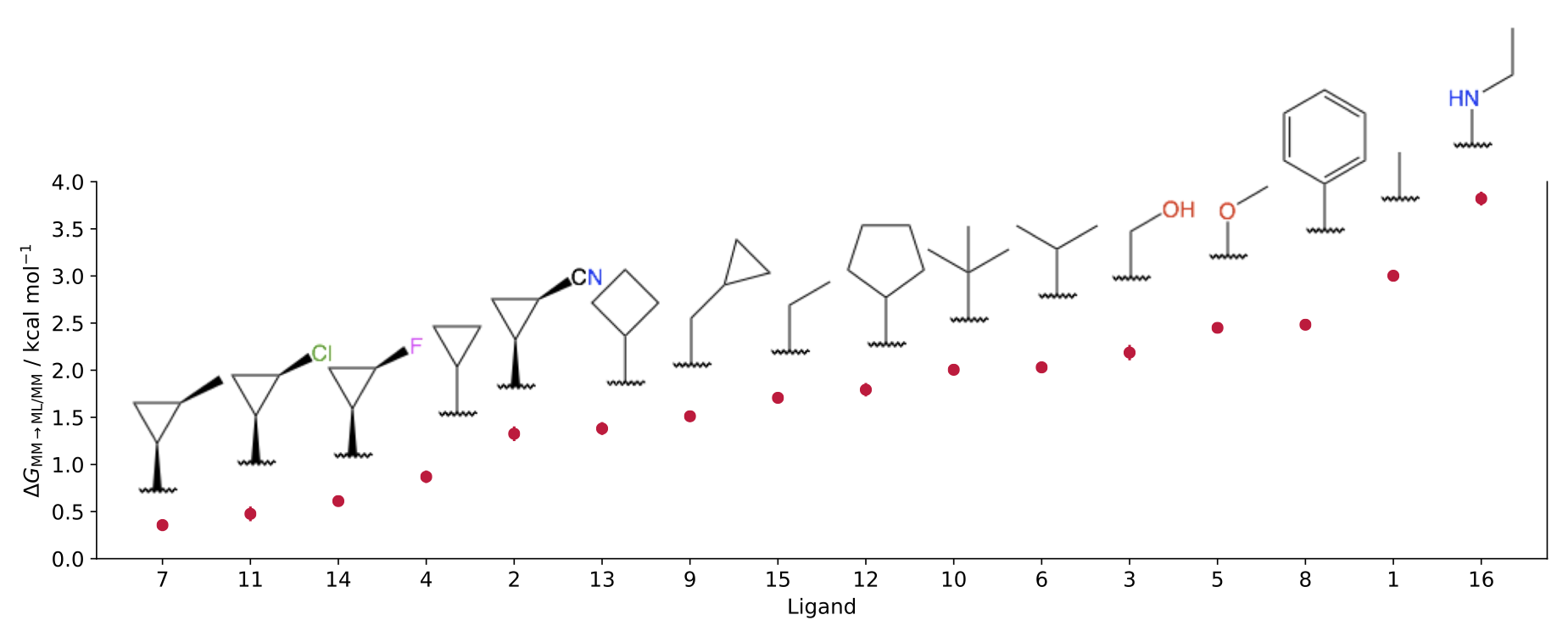
図5: 各リガンドに対してのML/MMによる補正項の大きさの比較。論文[1] Fig. 7より。

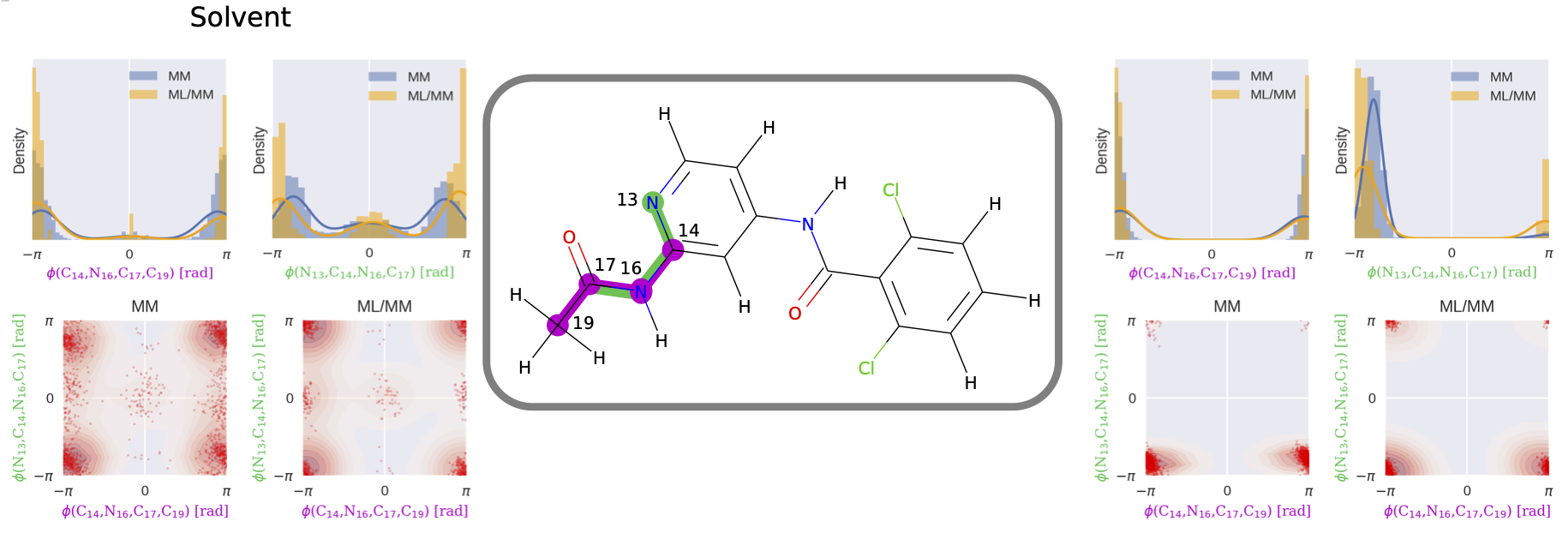
図6: MMとML/MMそれぞれのシミュレーションにおける、リガンド1の2箇所の二面角の分布の比較。論文[1] Fig. 8より。

化合物部分を古典力場からNNPに変化させるシミュレーションから計算される自由エネルギーはいずれも正の値であり、古典力場に比べて化合物のタンパク質に対する結合能を低く評価するものでした (図5) 。また、古典力場とNNPでは化合物の二面角の分布が大きく異なっており、これらのひずみエネルギーが古典力場とNNPの結合自由エネルギーの差に寄与し、精度改善につながったと考えられます (図6) 。

今回得られた結果からさらに精度を向上させるためには、リガンド部分を古典力場からNNPに変化させるシミュレーションの時間を長くすることで精度の向上を図るなどが考えられます。

今後の展望

今回紹介した手法では、MDシミュレーションに用いる力場の不正確性に伴う計算精度低下に対して、化合物部分にNNPを適用することで計算精度の向上を図るというものでした。しかしながら、今回の手法ではまだ解決に至っていない問題点があります。

一点目は、タンパク質-化合物の相互作用は古典力場近似のままである点です。
例えば、化合物と相互作用することで、タンパク側に電荷や分極が誘起され相互作用するケースが知られていますが、この現象を正確に扱うには、タンパク-化合物間相互作用もNNP等により正確に扱う必要があります。同様に、タンパク質内の相互作用をNNPでより正確に表現することで、間接的に計算精度が向上することも期待されます。
二点目は、MDシミュレーションによるサンプリングが不十分で不正確になってしまうケースでは、今回の手法では精度の向上が期待できないという点です。近年、このようなサンプリング問題に対しても深層学習を用いた手法が登場しており (例えばBoltzmann generator [6]) 、今後、深層学習によるブレークスルーが期待される分野の一つとなっています。

謝辞

約1ヶ月の間、例年とは異なるリモート環境の中でも社員の皆さまの手厚いサポートのおかげで不自由なく充実したインターン生活を送ることができました。実験系の研究室に所属していることもあり、本格的な開発を行うことが初めてであったため最初は不安もありましたが、社員の皆さまのおかげで毎日楽しく課題に取り組み目に見える形で成果を上げることが出来てとても嬉しく思います。
最後になりますが、メンターの石谷さん、副メンターの武本さん、および関係者の皆さまには期間中特にお世話になりました。この場を借りて御礼申し上げます。誠にありがとうございました。