拡散モデルを用いた自由エネルギーの推定

 

本記事は、2023年夏季インターンシッププログラムで勤務された坂部圭哉さんによる寄稿です。

はじめに

はじめまして，PFN 2023 夏季インターンシップに参加しました，東京大学 M1 の坂部圭哉です．普段は微分方程式を効率的に解く手法を研究しています．

今回の夏季インターンでは，拡散モデルを用いて自由エネルギーを推定する課題に取り組みましたので，本記事ではその詳細を説明したいと思います．

なお，インターン期間中では分子系の拡散モデルをうまく学習させることができず，なぜ学習できないのかという原因究明の解析に多くの時間を費やしました．
その関係で，本記事に紹介する理論や手法と，実際に原因究明の段階で行っていた実験手法には，様々な部分で差異があります．
予めご了承ください．

理論背景

自由エネルギーの推定

自由エネルギーとは，化学系の安定性を表す非常に重要な物理量です．
例えば，ある化学反応が進行するかどうかは，その反応によって自由エネルギーの総和が減少するかどうかで決まります．
また理論的には，自由エネルギーは完全な熱力学関数であることが知られており，微分などを行うことで系の熱力学的性質をすべて導出できることが知られています．
そのため，様々な分子の自由エネルギーを推定するタスクはとても重要な課題です．

しかし，分子動力学シミュレーションなど計算機実験の結果から自由エネルギーを直接推定することは後述の理由などにより難しく，その代わりの手法として，2つの分子の自由エネルギーの差分のみを推定する「自由エネルギー摂動法」などが使われてきました．

本インターンでは，他の分子からの差分ではなく，拡散モデルを用いて直接自由エネルギーを推定する手法の開発・実装を試みました．

Boltzmann 分布と分配関数・自由エネルギー

そもそも，自由エネルギーとは何でしょうか？
ここでは，Boltzmann 分布の導入から始めて説明したいと思います．
なお以下では，\(N\) はいま考えている分子の原子数，\(\beta\) は逆温度パラメタ (所与の定数)，\(\mathbf{x}\) は各原子の位置 (\(3N\) 次元ベクトル)，\(E(\mathbf{x})\) は各原子の位置が \(\mathbf{x}\) のときの分子のエネルギーを，それぞれ表すものとします．

標準的な (古典) 統計力学の理論において，エネルギーが \(E(\mathbf{x})\) であるような配置 \(\mathbf{x}\) が出現する確率は \(\exp(-\beta E(\mathbf{x}))\) に比例すると考えられています．
このように，「出現する確率が \(\exp(-\beta E(\mathbf{x}))\) に比例する」という分布を Boltzman 分布と言い，この式に登場する \(\exp(-\beta E(\mathbf{x}))\) を Boltzmann 因子と言います．
このとき，\(p(\mathbf{x})\) を全空間で積分すると \(1\) になる，すなわち

\(\int p(\mathbf{x})\mathrm{d}\mathbf{x} = 1\)

という要請から，Boltzmann 分布の確率密度関数 \(p(\mathbf{x})\) は，

\(p(\mathbf{x}) = \frac{\exp(-\beta E(\mathbf{x}))}{\int\exp(-\beta E(\mathbf{x}))\mathrm{d}\mathbf{x}}\)

と表現されます．
ここで，規格化定数として上式の分母に登場する量を分配関数と言い，\(Z\) で表します．
すなわち，

\(Z \mathrel{\mathop:}=\int\exp(-\beta E(\mathbf{x})) \mathrm{d}\mathbf{x}\)

であり，このとき

\(p(\mathbf{x}) = \exp(-\beta E(\mathbf{x}))/Z\tag{1}\)

です．
この確率密度関数を用いれば，統計的な物理量の平均値が得られます．
すなわち，物理量 \(A(\mathbf{x})\) の統計平均 \(\langle A\rangle\) は

\(\langle A\rangle \mathrel{\mathop:}= \int A(\mathbf{x})p(\mathbf{x})\mathrm{d}\mathbf{x} = \frac1Z \int A(\mathbf{x})\exp(-\beta E(\mathbf{x}))\mathrm{d}\mathbf{x} \tag{2}\)

によって得られます．

さて，統計的な物理量は式 (2) で与えられますが，これは多次元空間での積分を含んでおり，実際の数値計算において実用的ではありません．例えば，数値積分するために一定の間隔で点をサンプリングしようとしたとき，次元 \(3N\) に対して指数的に多くの点をサンプリングする必要が生じてしまいます．

そこで，このような統計平均を算出するためには，MCMC (Markov-chain Monte Carlo) 法などのサンプリング手法が用いられてきました．
これらのサンプリング手法においては，分布 \(p(\mathbf{x})\) に従うデータ \(\{\mathbf{x}^{(i)}\}_{1 \le i \le M}\) を擬似的に生成することで，

\(\langle A\rangle \simeq \frac1M\sum_{i = 1}^MA(\mathbf{x}^{(i)})\)

により統計平均を推定できます．

一方，統計物理学においては，規格化定数である分配関数 \(Z\) そのものも物理的に重要な意味を持ちます．
その最も代表的なものが自由エネルギー \(F\) であり，これは

\(F \mathrel{\mathop:}= -\beta^{-1}\log(Z)\)

により定義されます．
自由エネルギーは，系の安定性を表す極めて重要な物理量なのですが，統計平均の形式 (式 (2)) で表現できないために，MCMC などの手法を用いて推定することは非常に困難です．
従って従来は，自由エネルギーが既知である分子をもとにそれとの差分を推定する「自由エネルギー摂動法」などが使われてきました．

そこで本インターンでは少し視点を変え，分配関数 \(Z\) を求める代わりに，Boltzmann 分布の確率密度関数 \(p(\mathbf{x})\) を推定するという方針を考えます．
もし \(p(\mathbf{x})\) の推定値 \(\widetilde{p}(\mathbf{x})\) が得られれば，式 (1) より，分配関数 \(Z\) の推定値 \(\widetilde{Z}\) が以下の式によって得られると考えられるからです：

\(\widetilde{Z} \mathrel{\mathop:}= \exp(-\beta E(\mathbf{x})) / \widetilde{p}(\mathbf{x}). \tag{3}\)

なお，本インターンの手法では \(p(\mathbf{x})\) の推定に拡散モデルを用いるのですが，この部分の詳細は後の節に記します．

一般の分布における分配関数

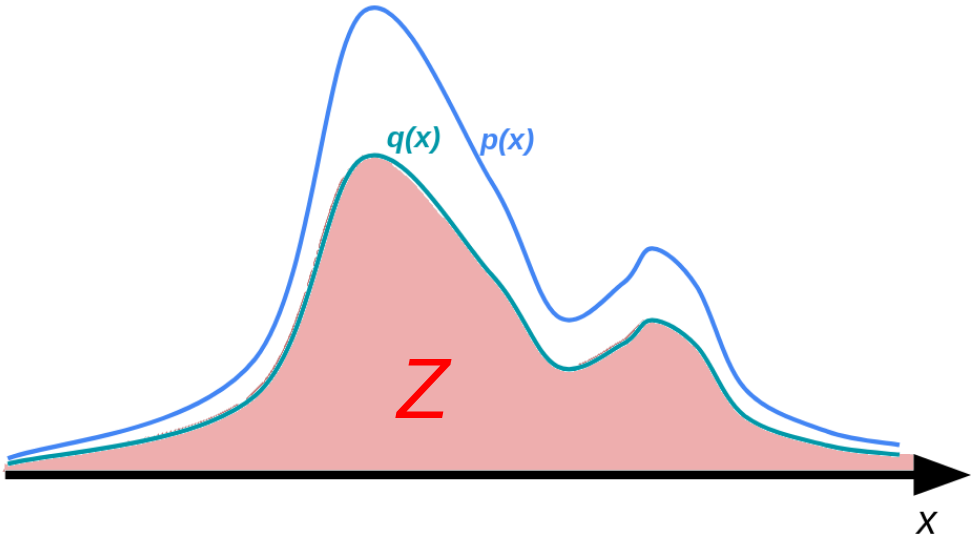
上記の分配関数という概念は，化学系に限らず一般の確率分布の規格化定数として考えられます．

確率分布の確率密度関数を \(p(\mathbf{x})\) とします．
確率密度関数はその定義から，全空間で積分すると \(1\) となります．つまり，

\(\int p(\mathbf{x})\mathrm{d}\mathbf{x} = 1\)

が成り立ちます．

ただし，非常によくあるケースとして，\(p(\mathbf{x})\) そのものは得られないが，これに比例する \(q(\mathbf{x}) \; (\propto p(\mathbf{x}))\) は各点で得られるという場合があります．
このような場合，

\(Z \mathrel{\mathop:}= \int q(\mathbf{x})\mathrm{d}\mathbf{x}\)

として分配関数 \(Z\) を考えます．いま \(\int p(\mathbf{x})\mathrm{d}\mathbf{x} = 1\) だったので，このときすべての \(\mathbf{x}\) において \(q(\mathbf{x}) = Zp(\mathbf{x})\) という関係が成り立ちます．
今回のテーマである，拡散モデルを用いた分配関数推定の手法は，このような一般の分布における分配関数の推定にも適用できます．

拡散モデル 〜overview〜

拡散モデルは，画像生成などの分野で近年盛んに用いられている生成系のモデルで，拡散過程の逆過程を再現することによって目的の分布に属するデータを生成します．
拡散モデルの理解には多様なものが存在しますが，ここでは「拡散過程によって分布が変化する」という視点に立って説明をします．

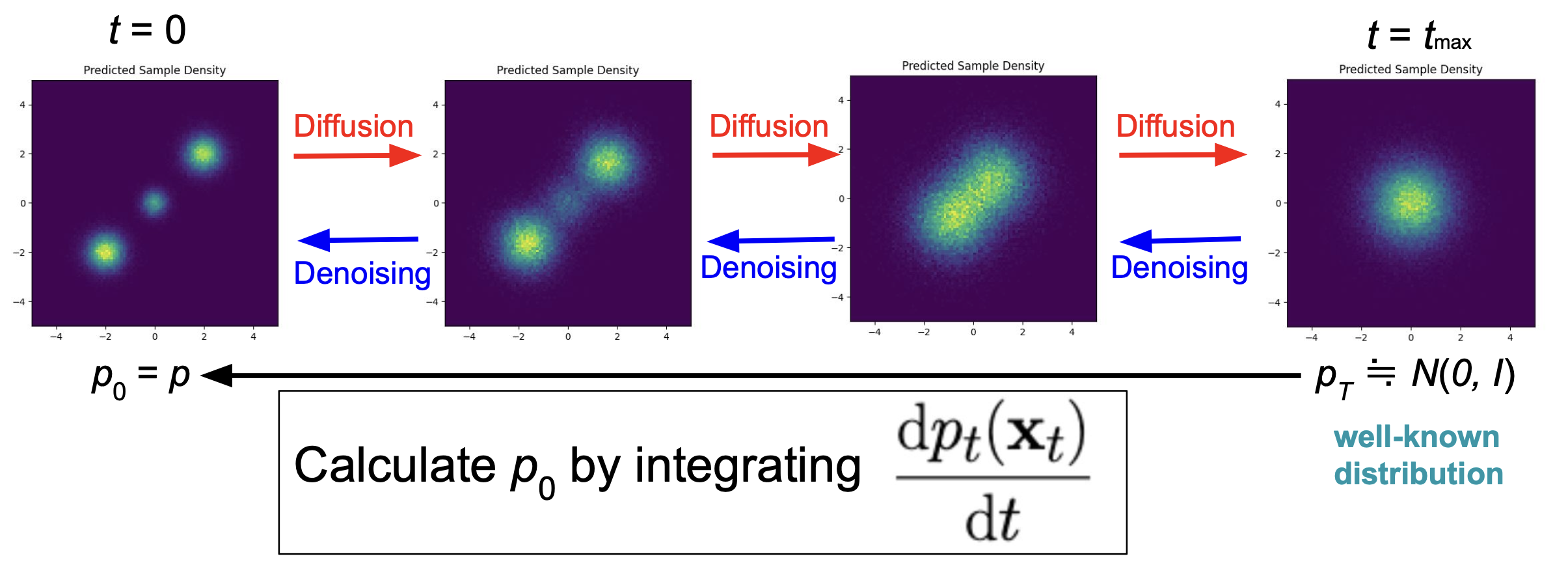
拡散過程においては時刻と呼ばれる概念が存在し (これを \(t\) で表します)，時間発展に伴って各データが拡散され，分布が変化すると考えます．
時刻 \(t = 0\) における分布は再現したい元の分布，\(t \to +\infty\) における分布は完全にノイズの分布 (i.e. 標準正規分布) となります．
拡散モデルにおいては，各時刻において「データをどのように微小移動させれば微小時間前のデータとみなせるか」ということを学習し，十分に大きな時刻から \(t = 0\) に戻す過程を再現することで最初の分布に従うデータを生成します．

拡散過程の数学的定式化

拡散過程の数学的定式化については様々なものがありますが (参考: [1]) ，ここでは，確率微分方程式による定式化を採用します．

拡散過程においては，各データ \(\mathbf{x}_t\) は次の確率微分方程式に従って時間発展するものとします：

\(\mathrm{d}\mathbf{x}_t = -\frac{\mathbf{x}_t}2 \mathrm{d}t + \mathrm{d}B_t. \tag{4}\)

ここで．\(B_t\) は標準正規ホワイトノイズ (Wiener 過程) と呼ばれる確率的な項で，この項の存在によりデータが拡散されます．
この式は，微小な時間発展に伴って，データがノイズを加えられながら (\(+\mathrm{d}B_t\)) 少しずつ縮小する (\(-\frac{\mathbf{x}_t}2 \mathrm{d}t\)) ということを表現しています．

この拡散過程の逆過程は，逆時間を \(\bar{t} \mathrel{\mathop:}= -t\) と表すこととして次の式により表されます (導出は [1] などを参照)：

\(\mathrm{d}\mathbf{x}_{\bar{t}} = \frac{\mathbf{x}_{\bar{t}}}2 \mathrm{d}\bar{t} + \nabla\log p_t(\mathbf{x}_{\bar{t}}) \mathrm{d}\bar{t} + \mathrm{d}B_{\bar{t}}.\)

従って，各 \((t, \mathbf{x})\) での \(\nabla\log p_t(\mathbf{x})\) さえ計算できれば上式の逆過程を再現することができます．
これを分野の専門用語でスコアと言い，\(\mathbf{s}_t(\mathbf{x}) \mathrel{\mathop:}= \nabla\log p_t(\mathbf{x})\) で表します．

さて，上の 2 式は各データの 1 点 1 点が従う時間発展方程式なのですが，これに対応して，各時刻の確率密度関数 \(p_t(\mathbf{x})\) が従う時間発展方程式が導出できます．これを，Fokker-Planck 方程式と言います：

\(\frac{\partial p_t}{\partial t} = \frac12\left(\mathbf{x}\cdot\nabla p_t + \nabla^2p_t + Dp_{t}\right). \tag{5}\)

なお上式において，\(D\) は \(\mathbf{x}\) の次元 (分子の場合 \(3N\)) であり，また記号 \(\nabla\) は \(\mathbf{x}\) 方向の微分を表しています．
この式より，スコアの従う微分方程式としては次の式が得られます：

\(\frac{\partial \mathbf{s}_t}{\partial t} = \frac12\nabla\left(\mathbf{x}\cdot \mathbf{s}_t + \|\mathbf{s}_t\|^2 + \nabla\cdot \mathbf{s}_t\right).\)

この式もまた Fokker-Planck 方程式と呼ぶこととします．

\(p(\mathbf{x})\) の計算とフローモデル

さて最初の目的を思い出すと，分配関数を計算するために各点での \(p(\mathbf{x}) \; (= p_0(\mathbf{x}))\) を求めたかったのでした．
そこで，拡散過程の考え方を用いて \(p(\mathbf{x})\) を求める考え方を説明します．

拡散モデルの重要な点の 1 つとして，\(p_t(\mathbf{x})\) の値を必要としないことが挙げられます．
逆過程の再現に必要なのは \(\mathbf{s}_t(\mathbf{x}) = \nabla\log p_t(\mathbf{x})\) のみであり，これは \(p_t(\mathbf{x})\) の定数倍の量 \(q_t(\mathbf{x})\) さえ分かっていれば計算が可能です．
この性質のおかげで，\(p(\mathbf{x})\) の値は分からなくても (つまり，規格化定数が分からなくても) \(q(\mathbf{x}) (\propto p(\mathbf{x}))\) さえ分かれば拡散モデルを学習することができます．

ただし，こうした性質の一方で，時刻無限大 \(t \to +\infty\) において分布は標準正規分布 \(\mathscr{N}(0, I)\) に収束し，それに伴って確率密度関数も \(p_t \to p_{\mathscr{N}(0, I)}\) (\(t \to +\infty\)) と収束します．
つまり，規格化定数が分からないという立場を取っていたはずなのですが，\(t \to \infty\) の極限における規格化定数は得られるのです．
このことから，時刻 \(t \to \infty\) の \(p_t(\mathbf{x})\) を時刻 \(t = 0\) での \(p_0(\mathbf{x})\) にうまく繋げることができれば，\(p_0(\mathbf{x})\) を求めることができそう，つまり，元の分布の規格化を行うことができそうです．

異なる時刻における \(p_t(\mathbf{x})\) を繋げるために，Fokker-Planck 方程式を用います．
式 (5) を変形すると，以下の式が得られます：

\(\frac{\partial\log p_t}{\partial t} = \frac12\left(\mathbf{x}\cdot \mathbf{s}_t + \|\mathbf{s}_t\|^2 + \nabla\cdot \mathbf{s}_t + D\right). \tag{6}\)

ただしここでも \(\mathbf{s}_t(\mathbf{x}) = \nabla \log p_t(\mathbf{x})\) です．
この式を積分することで，原理的には異なる時刻における \(p_t(\mathbf{x})\) の差分を計算することができます：

\(\log p_{t_1}(\mathbf{x}) – \log p_{t_0}(\mathbf{x}) = \int_{t_0}^{t_1}\frac{\partial\log p_t}{\partial t}\mathrm{d}t = \frac12\int_{t_0}^{t_1}\left(\mathbf{x}\cdot \mathbf{s}_t + \|\mathbf{s}_t\|^2 + \nabla\cdot \mathbf{s}_t + D\right)\mathrm{d}t.\)

十分に大きな時刻 \(t = t_\mathrm{max} \gg 1\) において \(p_{t_\mathrm{max}}(\mathbf{x}) \simeq p_{\mathscr{N}(0, I)}\) とみなすことで，

\(\log p_0(\mathbf{x}) \simeq p_{\mathscr{N}(0, I)}(\mathbf{x}) – \frac12\int_0^{t_\mathrm{max}}\left(\mathbf{x}\cdot \mathbf{s}_t + \|\mathbf{s}_t\|^2 + \nabla\cdot \mathbf{s}_t\right)\mathrm{d}t – \frac{Dt_\mathrm{max}}2.\)

により \(p_0(\mathbf{x})\) を推定することが可能だと考えられます．
ただし実際の推定においては，この式をそのまま用いるのではなく，下に述べるようにフローモデルの考えを取り入れて \(p_0(\mathbf{x})\) を推定します．

フローモデルとは，データが決定的に時間変化するような考え方の総称であり，各時刻・位置のフロー (ベクトル場) に沿ってデータが変化するように捉えられることからこのように呼ばれます．
これは，確率的なノイズが加わる拡散過程とは異なる考え方です．
ここでは天下りですが，データの時間変化が以下の式で表されるフローモデルを考えます：

\(\frac{\mathrm{d}\mathbf{x}_t}{\mathrm{d}t} = -\frac12\left(\mathbf{x}_t + \mathbf{s}_t(\mathbf{x}_t)\right). \tag{7}\)

ここで \(\mathbf{s}_t\) は，これまで述べてきた拡散過程により定義される \(\nabla\log p_t\) です．
実は，最初の分布 \(p_0\) が同じであるとき，このフローモデル (7) は，拡散過程 (4) と全く同じ分布を与えることが示せます([1], [2]式(7))．
従って，分布に従うデータを生成するとき，逆拡散過程を再現するのではなく，このフローモデルによって生成することも可能です．

それでは，このフローに沿った \(p_t\) の時間変化，つまり，\(\frac{\mathrm{d}\log p_t(\mathbf{x}_t)}{\mathrm{d}t}\) (ただし，\(\mathbf{x}_t\) は式 (7) の解) を考えてみましょう．
すると，式 (6), (7) を用いることで，

\(\frac{\mathrm{d}\log p_t(\mathbf{x}_t)}{\mathrm{d}t} = \left.\frac{\partial\log p_t(\mathbf{x})}{\partial t}\right|_{\mathbf{x}=\mathbf{x}_t} + \frac{\mathrm{d}\mathbf{x}_t}{\mathrm{d}t}\cdot\nabla\log p(\mathbf{x}_t) = \frac12\nabla\cdot \mathbf{s}_t(\mathbf{x}_t) + \frac D2\)

のように計算できます．
従って，

\(\log p_0(\mathbf{x}_0) \simeq \log p_{\mathscr{N}(0, I)}(\mathbf{x}_{t_\mathrm{max}}) – \frac12\int_0^{t_\mathrm{max}}\nabla\cdot \mathbf{s}_t(\mathbf{x}_t)\mathrm{d}t – \frac{Dt_\mathrm{max}}2. \tag{8}\)

により \(p_0\) を推定することが可能です．

手法

拡散モデルの学習

拡散モデルを取り扱うにあたり，モデルをどのように学習させるかというところが 1 つ重要な点となります．
インターン期間中では，十分に大きな終了時刻 \(t_\mathrm{max}\) を適当に定め，時刻 \(t\) が \(0 \le t \le t_\mathrm{max}\) の範囲で正しい \(\mathbf{s}_t(\mathbf{x}) = \nabla\log p_t(\mathbf{x})\) を予測するモデルを学習させました．
この学習は，以下の 3 つの loss を最小化することにより行いました．

– \(L_{\mathrm{force}} \mathrel{\mathop:}= \mathbb{E}_\mathbf{x}[\|\mathbf{s}_0(\mathbf{x}) – \nabla\log p_0(\mathbf{x})\|^2]\)
– \(L_{\mathrm{inf}} \mathrel{\mathop:}= \mathbb{E}_\mathbf{x}[\|\mathbf{s}_{t_\mathrm{max}}(\mathbf{x}) + \mathbf{x}\|^2]\)
– \(L_{\mathrm{FP}} \mathrel{\mathop:}= \mathbb{E}_t\left[\mathbb{E}_\mathbf{x}\left[\left\|\frac{\partial \mathbf{s}_t}{\partial t} – \frac12\nabla\left(\mathbf{x}\cdot \mathbf{s}_t + \|\mathbf{s}_t\|^2 + \nabla\cdot \mathbf{s}_t\right)\right\|^2\right]\right]\)

ここで，\(L_{\mathrm{force}}\) は時刻 \(t = 0\) においてモデルが正しい分布のスコアを学習することを，\(L_{\mathrm{inf}}\) は時刻 \(t = t_\mathrm{max}\) においてモデルが正規分布のスコアを学習することを保障するものであり，\(L_{\mathrm{FP}}\) はその間の時刻においてモデルの出力が Fokker-Planck 方程式に従うことを要請するものです．
なお上記の関数に登場する偏微分などは，すべてPyTorchの自動微分を用いて計算しました．
なお，[2] においては \(L_{\mathrm{force}}\) と \(L_{\mathrm{FP}}\) の \(2\) つの loss のみが提案されていましたが，後述の 2 次元系で実験したところ，\(L_{\mathrm{inf}}\) を含めた方が良いことが分かりました．

なお，これらの loss は画像を生成する拡散モデルなどで通常使われているものとは全く異なるものです．
通常の拡散モデル ([3] など) の学習においては，学習データとして分布に従う点群を準備します．
そして，学習データに様々な大きさのノイズを加えた点を生成し，ノイズの加わった点をインプットとして加えられたノイズを推定する，という手法がよく取られます．
画像生成のような問題設定の場合は，元の分布はデルタ分布的なものとして考えられ，次元の低い多様体上にのみ分布が存在すると考えられるため，時刻が \(t = 0\) でのスコアは非常に特異的なものとなります．
しかし，Boltzmann 分布においては全空間で正の確率密度が存在するため，時刻 \(t = 0\) でのスコア \(\mathbf{s}_0(\mathbf{x}) = \nabla\log p(\mathbf{x})\) を学習することが可能です．
従って \(t = 0\) でのスコアも正しく学習したいのですが，このような場合にノイズを推定する学習を行うと，時刻 \(t = 0\) におけるスコアの精度が悪くなってしまう様子が観察されるようです [4]．
従って今回の課題では，ノイズを推定する学習ではなく，上記の 3 つの loss の最小化という学習手法を採用しました．

学習データの生成

拡散モデルの学習においては，\(L_{\mathrm{force}}\) の式に含まれる \(\nabla\log p(\mathbf{x})\) のデータが必要になります．

今回，下図に示される 2 次元混合ガウス分布のデータと，分子の例として一酸化炭素のデータを準備しました．

 

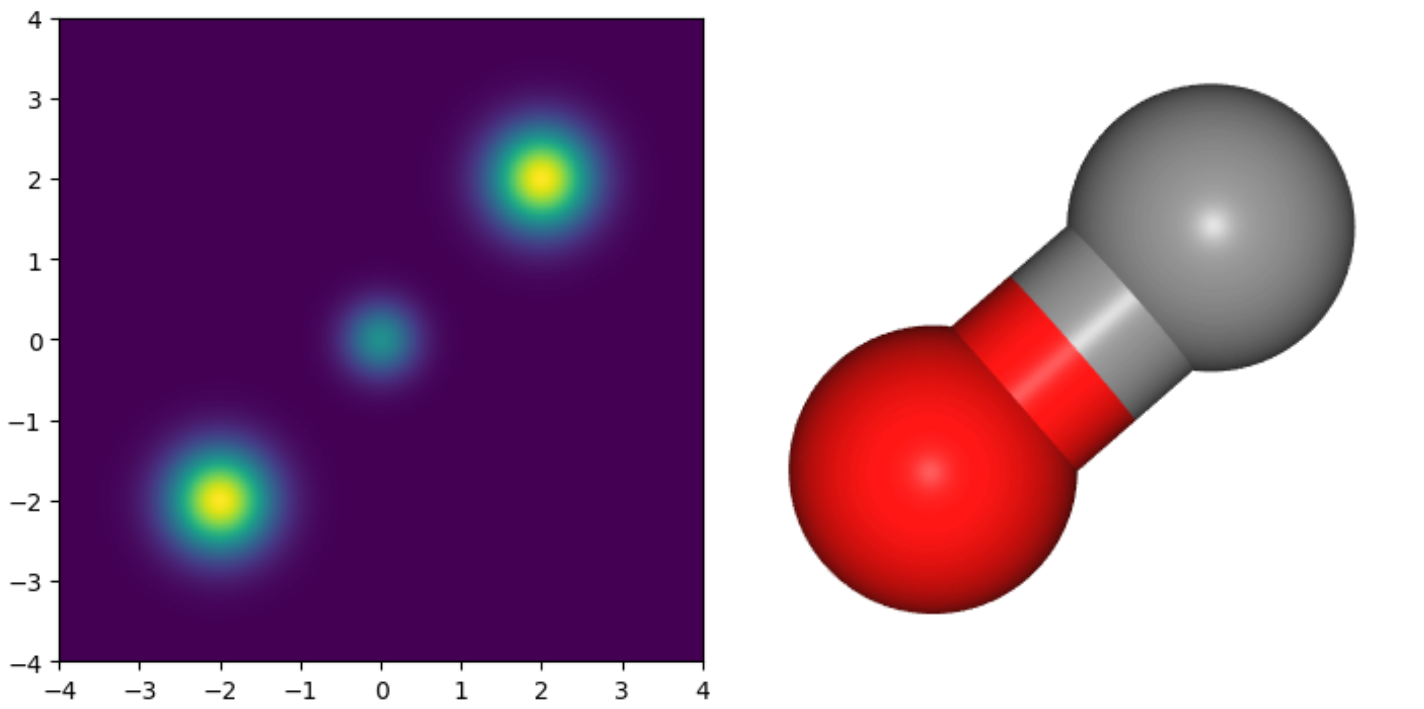
混合ガウス分布については，\(\nabla\log p(\mathbf{x})\) の値が理論的に求まるため，図に示される \([-4, 4] \times [-4, 4]\) の範囲を \(800 \times 800\) 個の格子に区切り，そのグリッドの各点で \(\nabla\log p(\mathbf{x})\) を計算して学習データとしました．

一酸化炭素については，G2 データセット [5] から一酸化炭素分子の各原子の座標を取得し，それを PFP (PreFerred Potential) [6] を用いて高速に分子動力学シミュレーションをすることで，\(10^5\) 個の点を生成しました．
これらの点におけるエネルギー勾配 \(\nabla E(\mathbf{x})\) が PFP により得られるため，このとき温度 \(T\) (あるいは逆温度 \(\beta\)) のときの対数密度勾配は \(\nabla\log p(\mathbf{x}) = -\beta\nabla E(\mathbf{x}) = -\nabla E/(k_\mathrm{B}T)\) として得られます．
なお，この分子動力学シミュレーションは温度 \(T = 300\;\mathrm{K}\) の条件にて実行しました．

上記のように生成したため，2 次元の学習データは空間上に格子点状に存在しているのに対し，一酸化炭素のデータは確率の高い領域に集中して存在している，という差異があります．

結果

2 次元の分布における結果

上に示した 2 次元の混合ガウス分布について，拡散モデルを学習し，式 (7) を用いて点をサンプリングしました．
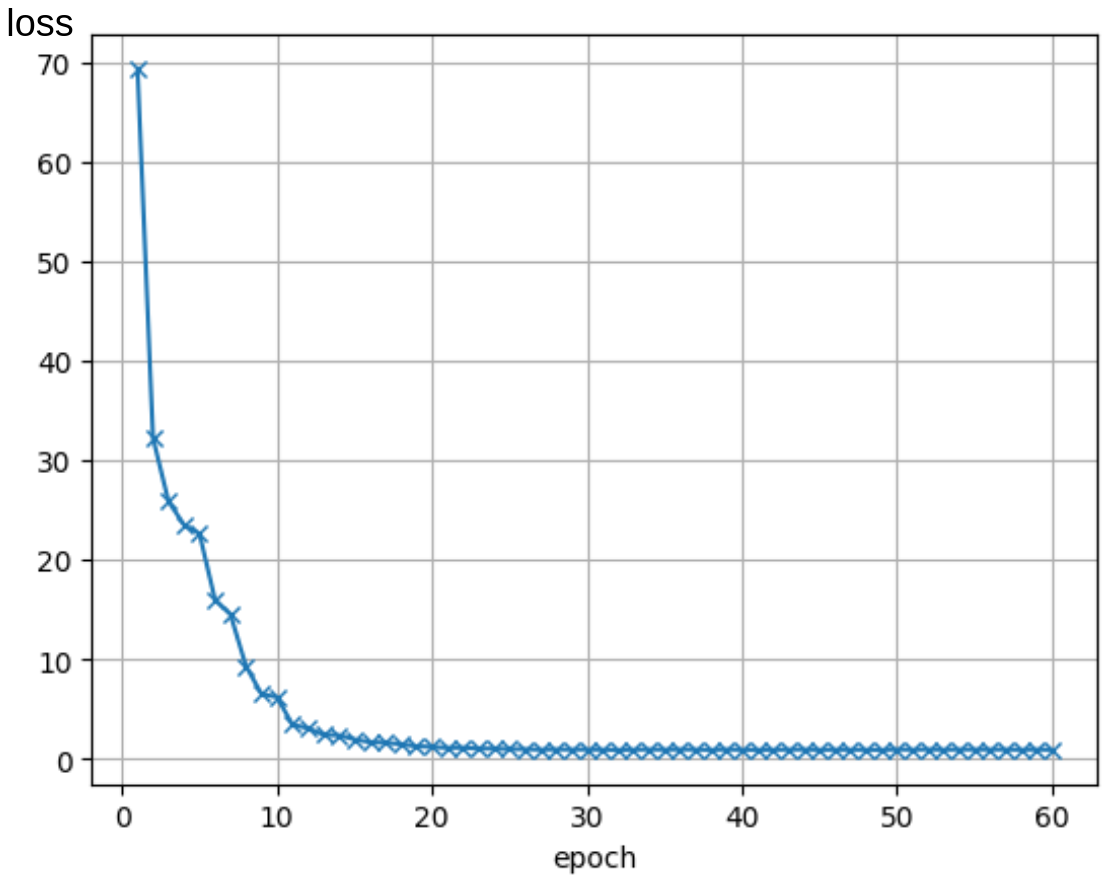
学習時の loss の変化を下図に示します．

また生成された点を 100 点プロットした図が下図になります．

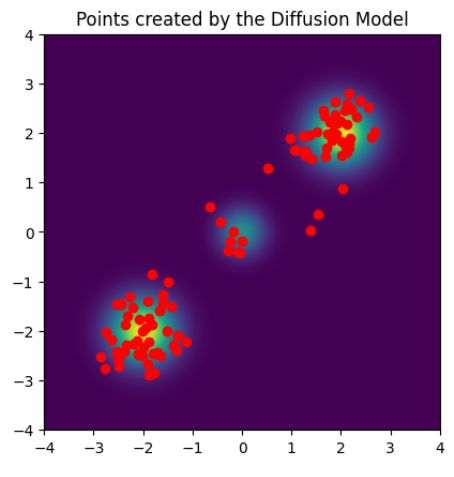
ほぼ学習元の分布に従った点が生成されている様子が確認できます．

こうして生成された点を用いて，この系の分配関数を提案手法により推定しました．
なお，はじめから規格化された分布を考えたため，この系においては \(Z = 1, \log Z = 0\) が厳密値となります．
生成された 1,000 点において，各点で \(\log Z\) の推定値 \(\log\widetilde{Z}\) を求めました．
そのヒストグラム下図に示します．

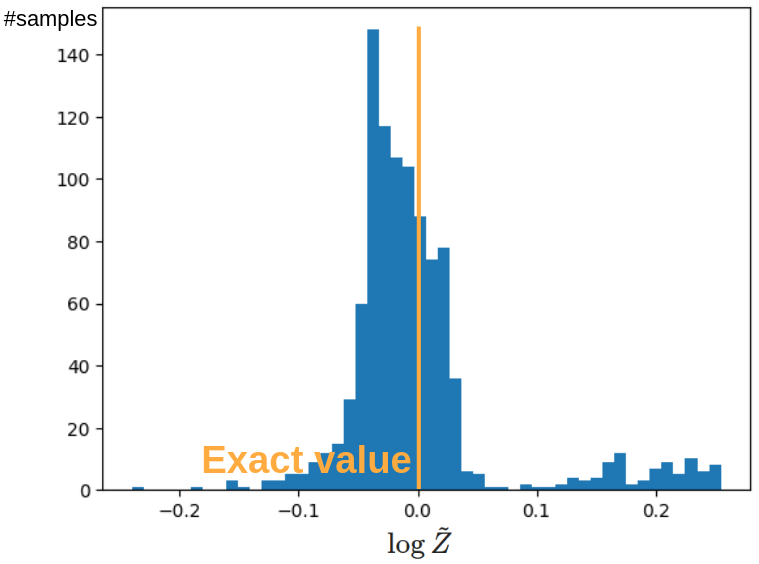
正しい値の周囲に大きなピークを持つような分布になっており，また大きな外れ値なども見られないため，概ね理論通りに分配関数の計算に成功していると考えられます．

なお実際に分配関数の推定に用いる際は，複数の点で推定値を出してその平均値を採用するような使用法になると考えられます．
従って，上図のデータからランダムに 100 点ずつ取ってブートストラップ法により平均値を推定しました．
そのヒストグラムが下図になります．

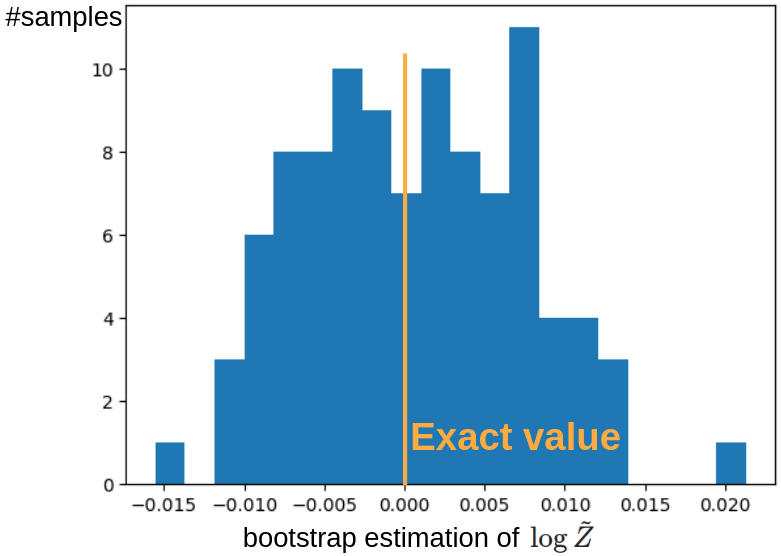
問題なく，正しい値をほぼ中央に持つような分布となっていることが確認できます．

分子系における結果

最も単純な分子として，二原子分子である一酸化炭素 (CO) の Boltzmann 分布を対象に学習を試みました．
様々にパラメタを変えて学習を試しましたが，本インターン期間中にはうまく学習させることができませんでした．
ここで，「学習がうまくいかなかった」とは，学習時に train loss が十分な減少を見せなかった，ということです．

そこで，なぜ学習がうまくいかないかを調べるため，次のような簡単な状況設定における学習実験を行いました．

– 時刻は \(t = 0\) しか考えない．つまり，\(L_{\mathrm{inf}}\) は考えない上，Fokker-Planck 方程式も \(t = 0\) のみで合わせる．
– 学習のデータ点は 2 点しか与えない．つまり，loss の式に登場する \(\mathbb{E}_\mathbf{x}[\cdot]\) というところを，特定の 2 点 \(\mathbf{x}^{(1)}, \mathbf{x}^{(2)}\) での値の平均として与える．
– 上記 2 条件によりデータ数が減りミニバッチを使わず loss の計算が確率的でなくなったため，学習時の最適化アルゴリズムにはよく使用される Adam ではなく，準ニュートン法の一種である L-BFGS 法を採用．

こうした設定のもとパラメタを様々に変えて学習実験を行いましたが，特に興味深い結果が得られたものに以下の表に示すものが挙げられます．
なお，学習時に与えた 2 点 \(\mathbf{x}^{(1)}, \mathbf{x}^{(2)}\) はすべての条件で等しく，使用したモデルなど諸条件も同一としました．
また参考として，2 次元のデータを用いて同様の (\(t = 0\) で 2 点のみの) 学習を行った結果も併記しておきます．

条件	1st iteration の loss	最終的な loss
\(T = 300 \;\mathrm{K}\)	28.1	22.9
\(T = 3\,000 \;\mathrm{K}\)	0.312	0.00112
\(T = 300 \;\mathrm{K}\),  \(\nabla \|\mathbf{s}_t\|^2\) 項なし	2.34	8.58e-11
(参考) 2 次元の分布	0.120	0.00164

それぞれの条件で学習したときの，学習曲線 (学習 step 数に対する loss の変化) は下図の通りです．

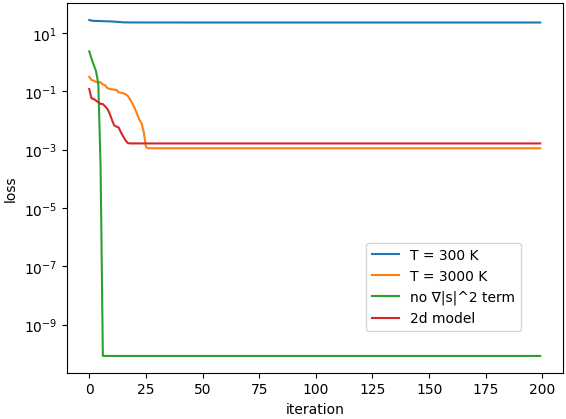
この表においては，まず系の温度 \(T\) の値を変化させています．
Boltzmann 分布においては，\(L_{\mathrm{force}}\) において学習すべきスコア \(\nabla\log p(\mathbf{x})\) が \(\nabla\log p(\mathbf{x}) = -\nabla E(\mathbf{x})/(k_\mathrm{B}T)\) と表されるので，\(T = 300 \;\mathrm{K}\) の条件は \(T = 3000 \;\mathrm{K}\) の条件に比べて 10 倍大きなスコアを学習することに相当します．
実際，上記の表の 1 行目 (\(T = 300 \;\mathrm{K}\)) と 2 行目 (\(T = 3000 \;\mathrm{K}\)) を比較すると，\(T = 300 \;\mathrm{K}\) の条件は \(T = 3000 \;\mathrm{K}\) と比較して loss の下がり方がかなり悪いことが読み取れます．
このことから，今回の loss 関数のもとでは，大きなスコアを学習することは困難な課題であることが分かります．

また大きなスコアを学習することが困難である要因として，\(L_{\mathrm{FP}}\) の中にスコアの 2 乗の項 (\(\nabla \|\mathbf{s}_t\|^2\)) の存在が挙げられるのではないかと考えました．
スコアが大きい条件では，特に 2 乗の項が大きくなりやすいと考えられるからです．
そこで，この \(\nabla \|\mathbf{s}_t\|^2\) の項を形式的に無くして学習をさせてみたところ，上表の第 3 行に表されるように大幅に学習が改善されました．
このことから，確かに \(\nabla \|\mathbf{s}_t\|^2\) 項が学習が困難である 1 要因であることが分かりました．

また上記のような実験以外に，\(L_{\mathrm{force}}\) と \(L_{\mathrm{FP}}\) のいずれか片方のみを学習するタスクや，1 点のみで学習するタスクも行ったのですが，これらは比較的容易なようでした．
実際，以下のような条件では容易に学習を成功させることができました．

– 多点で \(L_{\mathrm{force}} + L_{\mathrm{inf}}\) のみを減少させる (つまり，微分を見ずにスコアのみを合わせる)
– 多時刻・多点で \(L_{\mathrm{FP}}\) のみを減少させる (この場合，ほぼ \(\widetilde{\mathbf{s}}_t \simeq 0\) を出力するニューラルネットができあがります)
– (2 点ではなく) 1 点で \(L_{\mathrm{force}}\) と \(L_{\mathrm{FP}}\) を同時に減少させる．

以上の事柄を総合すると，2 点以上で \(L_{\mathrm{force}}\) と \(L_{\mathrm{FP}}\) を同時に減少させようとすると学習が難しくなり，特にスコアのノルムが大きい条件において \(\nabla \|\mathbf{s}_t\|^2\) 項が大きくなりがちであることが学習を困難にしている，と言えるのではないでしょうか．

残っている課題

一酸化炭素における上記の実験の結果として，2 点における学習は \(T = 3\,000 \;\mathrm{K}\) ならば可能であることが確認されました．
実際，\(T = 3\,000 \;\mathrm{K}\) における最終的な loss の値は 2 次元の分布を用いて同様の実験を行った場合の値と同程度であり，従って 2 次元で学習が成功したのと同様に \(T = 3\,000 \;\mathrm{K}\) では成功することが期待されました．

そこで，\(T = 3\,000 \;\mathrm{K}\) の条件において，2 点のみではなく，生成した \(10^5\) 個の点すべてを用いるという条件に変更し，Adam で学習を行いました．
時刻が \(t = 0\) のみであるという条件はそのままです．
この学習曲線を下図に示します：

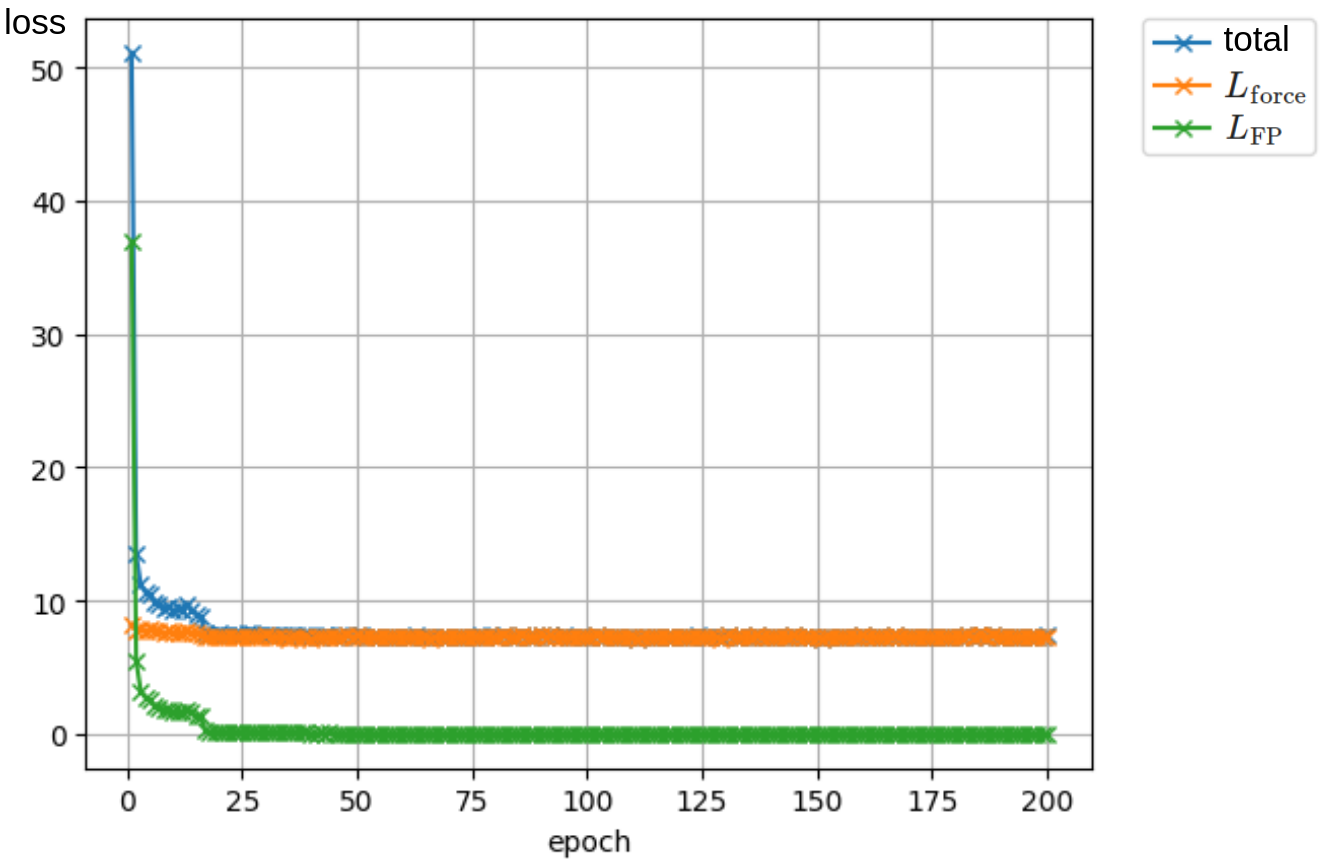
上図において，橙が \(L_{\mathrm{force}}\)，緑が \(L_{\mathrm{FP}}\) で，青がその合計です．
結果として，多点にすると 2 点のとき可能だった学習に失敗し，特にこの例では \(L_{\mathrm{force}}\) が減少しないことが分かります．

その要因を調べたところ，\(L_{\mathrm{force}}\) のみを学習させた場合において \(\left\|\nabla(\mathbf{s}_0\cdot \mathbf{x} + \|\mathbf{s}_0\|^2 + \nabla\cdot \mathbf{s}_0)\right\|\) の値が \(10^3\) 程度と非常に大きくなっていることが判明しました．
従って，\(t = 0\) での正しい分布においては Fokker-Planck 方程式に登場する \(\nabla(\mathbf{s}_0\cdot \mathbf{x} + \|\mathbf{s}_0\|^2 + \nabla\cdot \mathbf{s}_0)\) が非常に大きいため，ニューラルネットワークにとって扱いづらいものになってしまっている，という可能性が考えられます．

更なる解析や改善策を試したかったのですが，インターン期間が限られていたこともあり，詳細な解析を行うことはできませんでした．
例えば，\(\nabla(\mathbf{s}_0\cdot \mathbf{x} + \|\mathbf{s}_0\|^2 + \nabla\cdot \mathbf{s}_0)\) に含まれる 3 つの項のうちどれが大きいのか，という解析をすることによって理解が深まることは十分に考えられますし，また一酸化炭素分子の分布は比較的単純なので理論的にそれらの項の大きさを予測することもできそうです．
またこの空間微分の項を小さくする解決策としては，Å ではなく pm を使用するなど空間方向の単位系を変える手段が考えられます．
この単位系の変更は，拡散過程において加えるノイズのスケールを小さくすることに対応します．

また，2 次元の分布と一酸化炭素の違いを考えれば，分布の形状にも差異があるように思います．
実際，2 次元の分布は複数の点の周辺に分布を持つ，0 次元的な点ベースの分布であるのに対し，一酸化炭素は空間回転に対して対称な，球面型の 2 次元的な分布になっています．
こうした分布の形状といった事柄も学習の難しさに影響している可能性が考えられます．

技術的詳細

使用したモデルや，行った実験の詳細を記します．

まず 2 次元の分布の学習について，このとき用いたモデルは下の図に示す ResNet 型のものです．

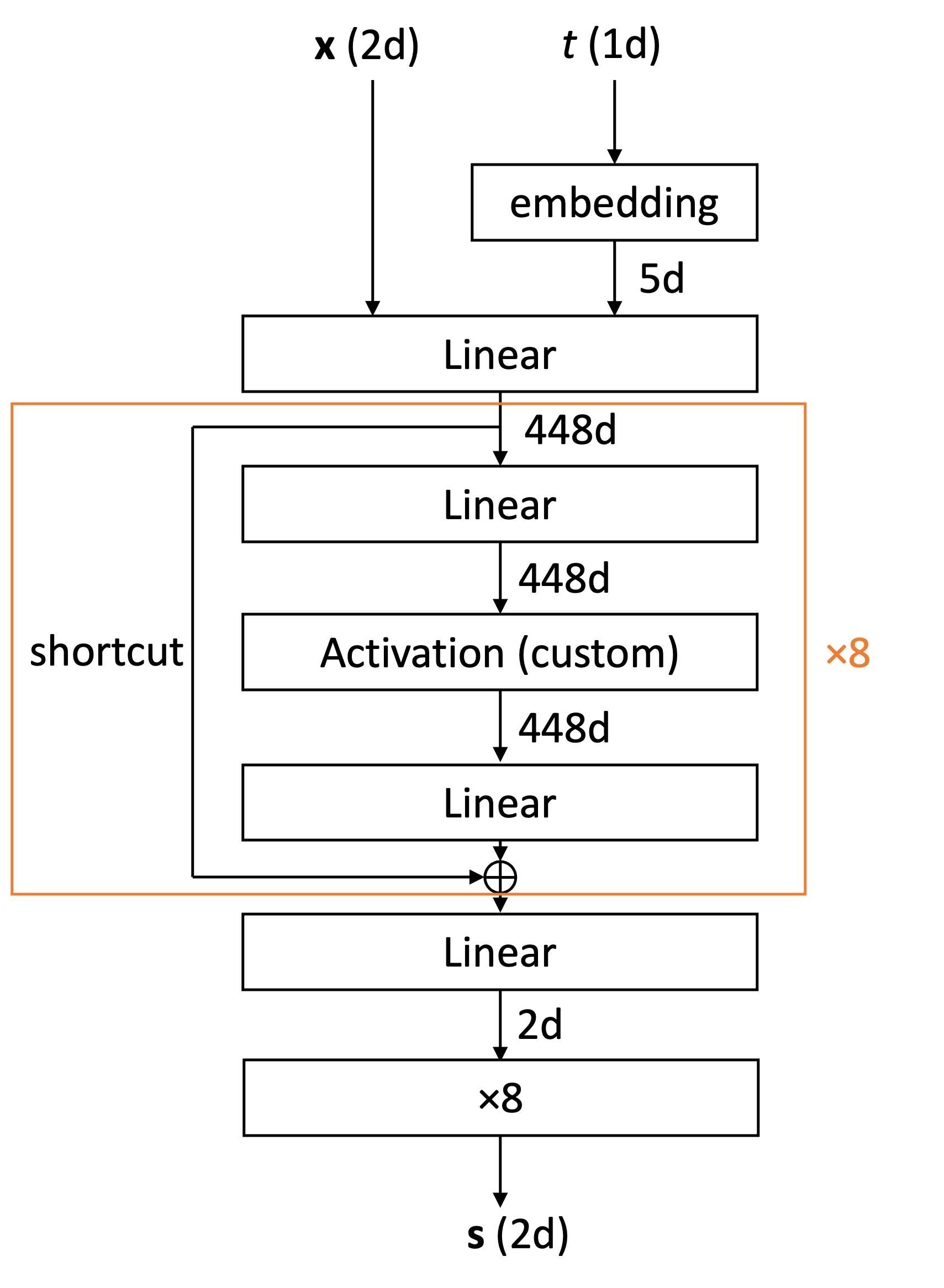
このモデルにおいて，活性化関数としては，下に示す自作のものを用いました：

\(f_\mathrm{activation}(x) = \begin{cases}x & (x \ge 0)\\\exp\left(x – \frac{x^2}2\right) – 1 & (x < 0)\end{cases}\)

この活性化関数を図示すると下図のようになります．

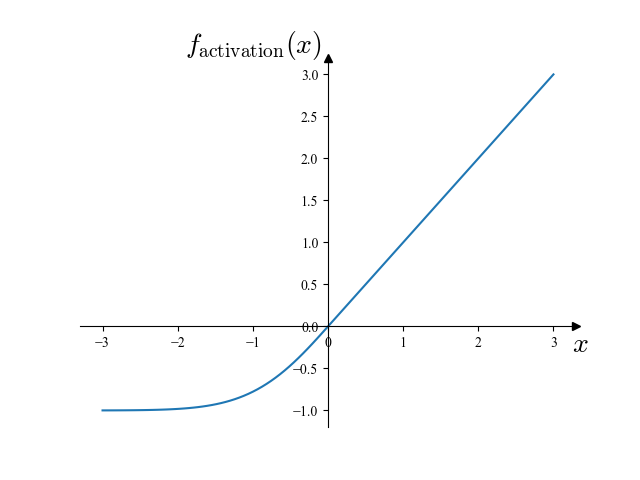
この関数は，Fokker-Planck 項において二階微分が存在することから \(C^2\) 級 (2 階微分連続) であるという要請を満たしつつ，学習時に最大三階微分を計算することから高階微分の計算が重くならないよう考慮して設計したものです．
また実際に学習において，GELU 関数を用いた場合と比較して loss の収束が良かったことを確認しました．

また 2 次元の分布の学習においては，loss 関数として \(L_\mathrm{force}, L_\mathrm{inf}, L_\mathrm{FP}\) の他に，以下の \(L_\mathrm{rot}\) を加えたものも実験しました：

\(L_\mathrm{rot} \mathrel{\mathop:}= \mathbb{E}_t\left[\mathbb{E}_\mathbf{x}\left[\sum_{i \neq j}\left\|\frac{\partial(\mathbf{s}_t)_j}{\partial x_i} – \frac{\partial(\mathbf{s}_t)_i}{\partial x_j}\right\|^2\right]\right].\)

この項は，本来 \(\mathbf{s}_t(\mathbf{x}) = \nabla\log p_t(\mathbf{x})\) は外微分が 0 (3 次元ベクトル解析の言葉で言えば，rot が 0) となるはずであることから，実際に外微分が 0 となることを要請するものです．
この項を加えてもよく学習することができましたが，この項無しでも既に分布をよく再現するモデルが学習できていたことから，この項を入れることの善悪に関して現段階では判断できません．

一酸化炭素の学習に関しては，様々なモデルを使用して試しましたが，特に上の表の結果を得たモデルは 2 次元の分布で用いたモデルとほぼ同型であり，2 次元のときとの差異は

– 入出力 (\(\mathbf{x}\) や \(\mathbf{s}\)) の次元を \(6\) に増やした点
– 中間層を \(704\) 次元に増やした点
– 最後に掛ける定数を \(8\) から \(50\) に変更した点
– 最後に，C 原子と O 原子にかかるスコアの総和が 0 となるよう，\(x, y, z\) 方向それぞれで両者の平均を引く処理を加えた点

の 4 点のみです．
またこのモデルの他にも，

– 位置 \(\mathbf{x}\) も embedding する
– 出力の形式を，方向とノルムに分離する
– 出力スコアが必ず CO の結合方向となるようなモデルの構造にする
– embedding の次元を増やす
– 浮動小数点の桁数を増やす

等といった工夫を試しましたが，学習の難易度が改善されていそうな雰囲気は感じませんでした．

また，他の文献 [2] において化学系の拡散モデルの学習に使用されている Graphormer3D というモデルも試しましたが，こちらに関しては温度 \(T = 3\,000\;\mathrm{K}\) で 2 点のみを学習するタスクも成功しませんでした．
ただし，こちらのモデルは設定可能なハイパーパラメータが非常に多く，ハイパーパラメータ次第では良いモデルとなる可能性も大いにあると考えています．

まとめ・今後の展望

本研究では，分配関数や自由エネルギーの推定を拡散モデルを用いて行う方法論を実際に計算機で実装し，PFP などの技術も活用しながら様々な実験を行いました．
その結果，2 次元の簡単なモデルケースでは問題なく分配関数を推定できたものの，一酸化炭素のデータにおいては拡散モデルを学習させる段階で様々な困難があることが判明しました．
今回用いた手法と，Stable Diffusion [7] などの成功を収めている画像生成モデルとの大きな違いの 1 つとして，学習時の loss 関数の違いが挙げられます．
画像モデルなどではノイズを学習させますが，本実験では Fokker-Planck 方程式を満たす解を学習するよう loss を設計しており，同じ拡散モデルの学習でありながらその内容は全く異なっていました．

本インターン期間中は，一酸化炭素のデータを用いた学習が困難だった理由の解析に多くの時間を割きました．
その結果，2 点のデータのみを学習する実験からは \(\nabla\|\mathbf{s}\|^2\) 項の存在が一因であると考えられ，学習すべきスコアのスケールを小さくすることで問題を回避できる可能性が示されました．
またより多くの点を用いた実験においても，Fokker-Planck 方程式中の空間微分項の値が \(10^3\) オーダーと非常に大きいことが分かり，これがニューラルネットにとって非常に扱いづらいものになっていたことが示唆されます．
この空間微分項の数値的なスケールを小さくするには，Å ではなく pm を使用するなど，空間方向の単位系を変更することによってこの問題を回避できる可能性があります．
また他にも分布の形状などが学習の難易度に影響を与えている可能性も考えられ，実際に何の要因による効果が最も大きいかを明らかにするためには，更なる実験を行う必要がありそうです．

また他に試す価値がある手法として，ノイズを予測する学習と Fokker-Planck 方程式とを組み合わせたり [2] [8]，スコアのノルムを合わせるのを諦めて方向のみを合わせる [2] といった方針も考えられるでしょう．
例えば方向のみを合わせる方法は，スコアの正しいノルムが出力できなくなることと引き換えに学習の難易度が下がることが期待できます．

また本記事の議論においては，式 (3) は，\(\widetilde{p}(\mathbf{x})\) が \(p(\mathbf{x})\) の推定値となっているときに \(Z\) の推定値を与える式として登場しました．
しかし，たくさんの点を取って式 (3) の平均値を \(Z\) の推定値とするという考え，すなわち

\(Z \simeq \mathbb{E}_\mathbf{x}[\exp(-\beta E(\mathbf{x}))/\widetilde{p}(\mathbf{x})]\)

という立場に立つと，これは全く異なる解釈が可能です．
いま，上式の \(\mathbb{E}_\mathbf{x}\) の部分には様々な平均の取り方が考えられるわけですが，もしここで \(\mathbf{x}\) の生成確率が \(\widetilde{p}(\mathbf{x})\) に従っていたとすると，この式は \(Z\) の Monte-Carlo 積分の表式を与えます．
なぜなら，

\(\mathbb{E}_{\mathbf{x} \sim \widetilde{p}(\mathbf{x})}[\exp(-\beta E(\mathbf{x}))/\widetilde{p}(\mathbf{x})] = \int\widetilde{p}(\mathbf{x})\exp(-\beta E(\mathbf{x}))/\widetilde{p}(\mathbf{x})\mathrm{d}\mathbf{x} = \int\exp(-\beta E(\mathbf{x}))\mathrm{d}\mathbf{x} = Z\)

と変形できるからです．
今回の手法においては，式 (7) を用いてデータを生成し，式 (8) を用いて \(\widetilde{p}\) を計算していたのでした．
実は，モデルの出力 \(\mathbf{s}_t(\mathbf{x})\) が \(\nabla\log p_t(\mathbf{x})\) に一致していなくとも，式 (8) は 式 (7) によるデータの生成確率を厳密に与えます．
従って今回の手法は，例えモデルが目的の分布 \(p(\mathbf{x})\) を正確に学習していなくても，分配関数 \(Z\) の不偏推定量を出力する厳密な手法であることが分かります．

従って，あまり精度の良くない拡散モデルを用いても \(Z\) の良い推定値が得られる可能性があるため，分配関数の推定は必ずしも高精度な拡散モデルが必要でない可能性があります．
ただし，精度の良くない拡散モデルを用いると \(\exp(-\beta E(\mathbf{x}))/\widetilde{p}(\mathbf{x})\) の分散が大きくなるため，\(Z\) の推定により多くのサンプリングが必要となることが予測される上，点がほとんどサンプリングされない領域がある場合に良い推定値とならないことが考えられます．
こうしたことを考察するため，あえて精度の悪い拡散モデルで分配関数 \(Z\) を推定し，その結果を評価する実験も行う意義がありそうです．

また，より根本的な話をするならば，拡散過程ではなく，初めからフローモデルの形で考えられないかという問題もあります．
実際，今回本当に我々が最終的に使用したものは，拡散過程そのものではなく，それと等価なフローモデル (7) だと考えることができます．
しかし，拡散過程から議論を出発してしまったために，Fokker-Planck 方程式において \(\nabla\|\mathbf{s}_t\|^2\) の項が現れてしまい，この項は学習が困難である一因になっていました．
従って，時間発展方程式に \(\nabla\|\mathbf{s}_t\|^2\) のような 2 乗の項が現れないような，新しいフローモデルを考えることができれば，より本問題が容易になる可能性がありそうです．

更に別の視点で捉えれば，今回は多変数関数の数値積分問題を解いたことになります．
従って，既存の数値積分手法との比較を行うことも非常に有益でしょうし，これまで確率密度だと考えられていなかった多変数関数の積分問題にも応用できる可能性があるのではないでしょうか．

終わりに

分配関数や自由エネルギーの計算というとても基本的な問題に対して拡散モデルを使用するという発想は非常に斬新で面白く，楽しみながら本課題に取り組むことができました．
私は普段は機械学習は全く使用しておらず，pytorch を使用するのも初めてだったのですが，メンターさんらが丁寧に教えてくださったため，スムーズに使い始めることができました．

近年，巷では「Deep でポン」などと揶揄されるように，ディープラーニングはビッグデータと強い計算資源さえ準備すれば容易に何でもできると思われている節が (少し) あるように思います (というか私はこのインターンに来るまでそう思っていました…)．
しかし，実際にはニューラルネットワークを期待通りに動作させることは非常に難しく，手を動かすことでそれを改めて実感するとともに，こうしたことに関連するノウハウが蓄積している PFN の強みや価値を改めて感じました．

また本インターンは昨年まではリモートメインでしたが，今年からは対面のイベントも多く復活しました．
主・副メンターの林さん・倉田さんの他，他のインターンメンバー・Chem チームのメンバーを中心にたくさんの方々と交流することができ，非常に良い機会となりました．
PFN では対面・オンライン問わず交流が非常に活発で，そうした雰囲気の中に入って空気感を体験できたことはとても貴重な機会でした．
特に，PFN は IT 企業ではあるのですが，情報系だけでなく，数学・化学・材料・機械・生物学など多様なバックグラウンドを持った人たちが集まり，知識を共有し，共同で仕事をしていて，とても面白い環境であると感じました．

参考文献