Blog

Home
Blog
aHSICを用いた多次元時系列上の変化検知と変数同定及びアルゴリズムの改善

2021.11.24

aHSICを用いた多次元時系列上の変化検知と変数同定及びアルゴリズムの改善

Area

Machine Learning / Deep Learning

Tag

# インターン

# 異常検知

Motoki Sato

Engineer

本記事は, 2021年度PFN夏季インターンシップで勤務した結城凌さんによる寄稿です.

はじめに

2021年度夏季インターンシップに参加した東京大学数理情報学専攻博士課程の結城凌と申します．今回のインターンシップでは変化検知および変数同定について取り組みました．

ロボティクス・医療・経済の様々な場面において，故障・病気・経済危機などの重大なリスクが存在し，これらを検知し未然に防ぎたいというニーズが古くから存在しています．そして，これらのリスクはセンサ値・診断データ・株価などの「変化」を伴うことが多いという特性があります．この特性を利用してリスクの検知に繋げる，変化検知というテーマが古くから研究されています(Basseville and Nikiforov, 1993)．近年その中の一つである変数同定というテーマが研究されています．これは，多次元の時系列データに対し，変化を検知するだけではなく，変化が発生している変数まで同定しようというテーマです．ここで，多次元時系列における変化検知で大きな問題となるのが，多次元時系列がスパース性を持ちうること(Barddal et al., 2017)，つまり変化が発生している変数が，次元数に比べ小さいことが想定されることです(図1)．例えば，先のロボティクスの例では，ロボット全体が壊れるというよりも，ロボットの一部の部品のみ故障するというケースが多いのではないかと考えられます．しかし，正常な変数に少数だけ混じっている，変化が発生している変数を同定するのは容易ではありません．

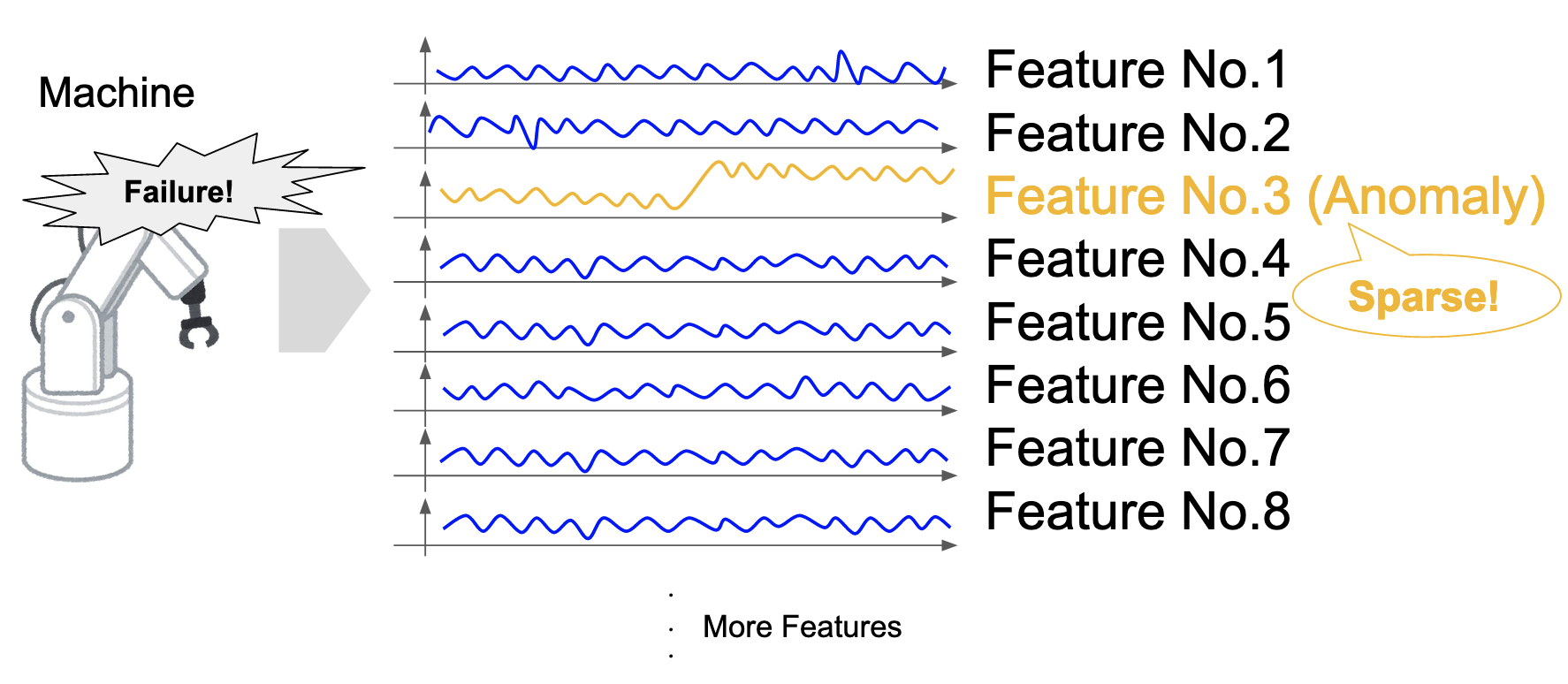
図1. 多次元時系列における変化のスパース性．

今回私は，カーネル法とLasso(Tibshirani, 1996; Tibshirani, 2011)に基づいた変化検知手法である，additive Hilbert-Schmidt independence criterion (aHSIC, Yamada et al., 2013)という手法を調査し，実装しました．そして，手法の性能を上げるためにアルゴリズムに次の改善を施しました．

改善点1: window内の複数の点の探索．
改善点2: 漸進的変化に対応するaHSICの拡張．
改善点3: 正則化係数 \(\lambda\) の自動調整．

最後に，手法の性能の改善を実験で確認しました．

手法

変化の定義

aHSICでは変化を次のように定義します．時系列データが従う \(d\) 次元確率変数を \(X\) とし，時刻 \(t\) のみが変化の候補点だとします．そして，時刻 \(t\) 以前で \(+1\), \(t\) より後で \(-1\) をとる確率変数 \(y\) を新たに定義します．この2つの確率変数を用いて， \(X\) と \(y\) が従属である場合に時刻 \(t\) は変化点であり，独立である場合に時刻 \(t\) は変化点ではないと定義します(図2)．このように新たな確率変数 \(y\) を人工的に定義することで，後述するようにLassoが使えるようになります．

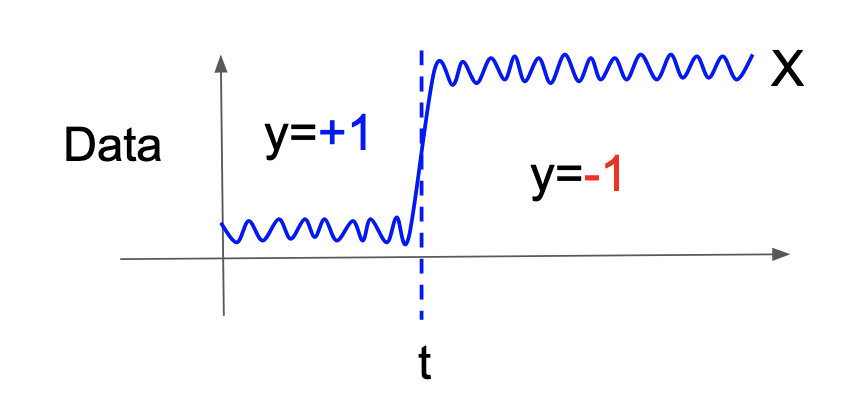
図2. 変化候補点と\(X\)，\(y\)．

aHSIC

aHSICは次の形で定義されます．
\[
\mathrm{aHSIC} (X,y)=\sum_{k=1}^d \alpha_k \mathrm{HSIC} (X_k,y).
\]

但しHSICは2つの確率変数の依存性を定量化した非負の尺度(Gretton et al., 2005)，\(X_k\) は \(X\) の \(k\) 次元目のデータを集めたもの，\(\alpha=(\alpha_1, \dots , \alpha_d)\) は非負で総和が \(1\) となる重みです．ここで重み \(\alpha\) の計算方法はいくつか考えられます(例: 全て \(1/d\) と設定する)が，次の最適化問題(HSIC Lasso, Yamada et al., 2014)を解くことで設定することを考えます．

\[
\min_{\alpha \in R^d} || \bar{L}-\sum_{k=1}^d \alpha_k \bar{K}^{(k)} ||_{Frob}^2 + \lambda ||\alpha||_1, \mathrm{s.t.} \ \alpha_1, \dots , \alpha_d \geq 0. \ (1)
\]

ここで，\(\bar{L}\) は \(y\) の中心化グラム行列，\(\bar{K}^{(k)}\) は \(X_k\) の中心化グラム行列(詳細な定義は原論文をご参照ください)，\(\lambda\) は正則化の強さを決める係数です．この最適化問題の第1項は次のように展開できます．

\[
|| \bar{L}-\sum_{k=1}^d \alpha_k \bar{K}^{(k)} ||_{Frob}^2 =\underline{\mathrm{HSIC} (y,y)}_{(1)} – \underline{2 \sum_{k=1}^d \alpha_k \mathrm{HSIC} (X_k,y)}_{(2)} + \underline{\sum_{k,l=1}^d \alpha_k \alpha_l \mathrm{HSIC} (X_k, X_l)}_{(3)}.
\]

各項の \(\alpha\) に関する最小化は次の意味を持ちます．

第1項: \(\alpha\) に関して定数なので無視できます．
第2項: HSICは非負なので，元々の最適化問題を最小化することは，\(X_k\) と \(y\) が独立なとき(\(X_k\) が変化を持たない時) \(\alpha_k\) を小さくすることを意味します．つまり，変化に無関係な次元が取り除かれることになります．
第3項: 元々の最適化問題を最小化することは，\(X_k\) と \(X_l\) が依存しているとき \(\alpha_k\) もしくは \(\alpha_l\) が小さくなることを意味します．つまり，変化に対して冗長な次元が取り除かれることになります．

以上をまとめると，変化に本質的に関わる次元に高い重みが置かれやすくなります．最後に，得られた \(\alpha\) を総和が \(1\) になるように正規化します．

Group Lasso

多次元時系列には，変数がグループ分けできるタイプのものが存在します．例としていくつかのパーツからなる機械を考えたとき，センサから得られた時系列の次元をパーツごとにグループ分けすることができます．ここで，次元1つ1つに正則化をかけるよりもむしろグループ単位で正則化をかけ，グループごとにまとめて \(\alpha\) を \(0\) にする(=変化のないグループ内の特徴量は同時に無視されやすくする)ことは自然な発想だと考えられます(図3)．これを実現するために，Group Lasso (Zou and Hastie, 2005; Meier, Geer, and Bühlmann, 2008)に基づくaHSICも提案されています．これは，先ほどの最適化問題の正則化項を変えるだけで簡単に実現できます (参考リンク)．

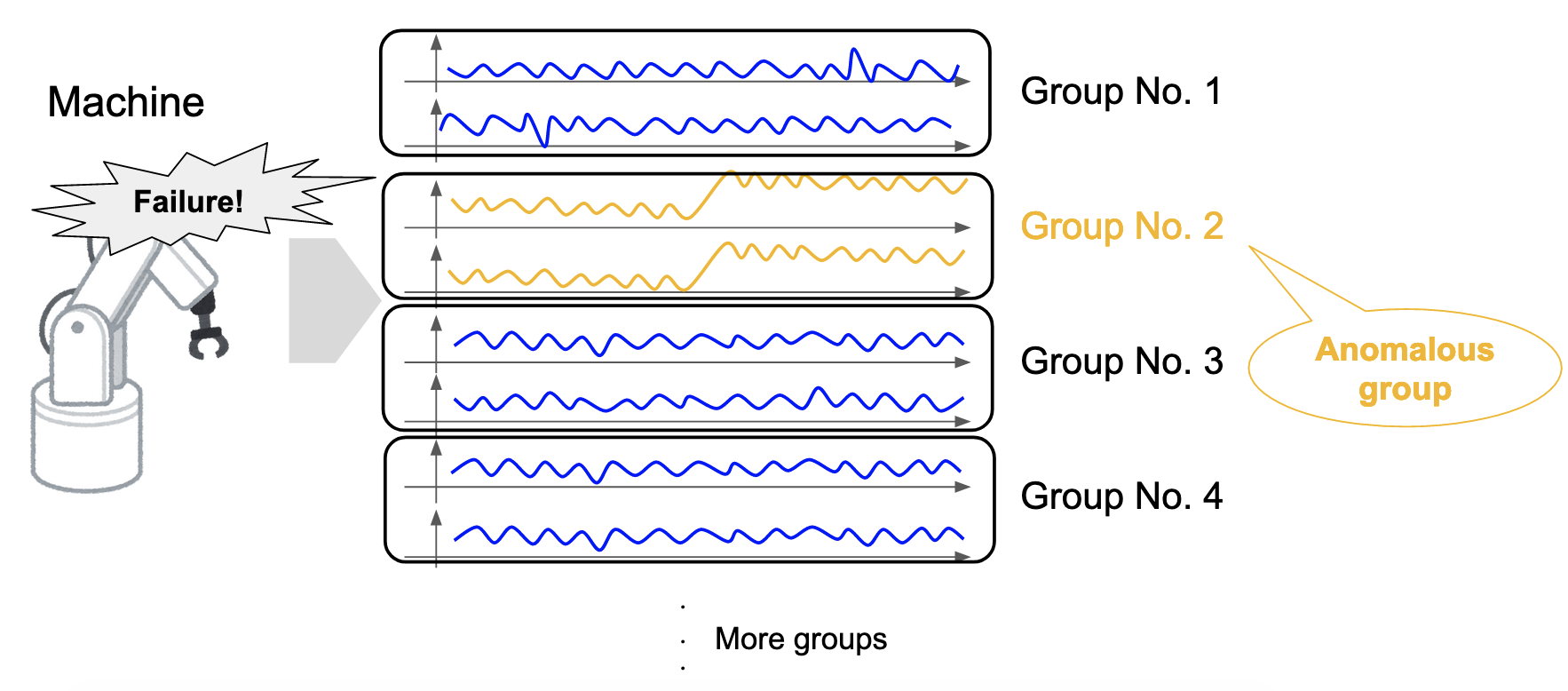
図3. Group Lassoの概念．

Sliding Windowアルゴリズム

実運用では変化点をリアルタイムで検出したいことがあります．そこで，これを実現するためsliding windowアルゴリズムを採用します(図4)．具体的には，時系列データから一定のサイズのデータ(window)を切り出し，windowの中心を変化候補点と仮定して変化スコアを計算します．そして，windowを一つずつずらしながら変化スコアを計算していくことを繰り返します．

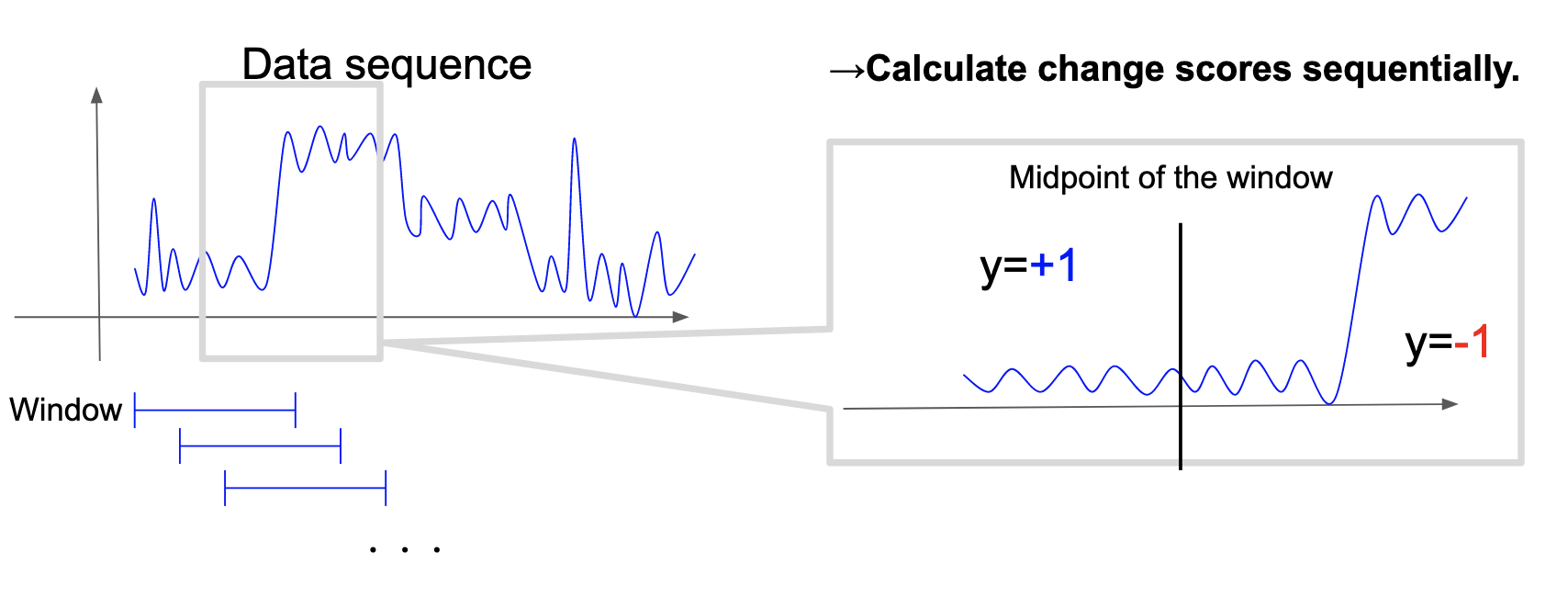
図4. Sliding Window アルゴリズム．

改善点

私が手法・アルゴリズムに施した改善は以下の3点にまとめられます．

改善点1: window内の複数の点の探索．
改善点2: 漸進的変化に対応するaHSICの拡張．
改善点3: 正則化係数 \(\lambda\) の自動調整．

改善点1. window内の複数の点の探索

原論文のアルゴリズムでは，windowの中間点のみを変化点と仮定して変化スコアを計算します．しかし，sliding windowアルゴリズムはその性質上，常に右側から最新のデータが入ってくるので，真の変化点と変化の候補点には常にギャップがあり，スコアの信頼性が落ちることになります．そこで，window内の様々な点を変化候補点と仮定し，変化スコアの最大値とそれに付随する貢献度を出力するようにアルゴリズムを変更しました．さらに，window内の全ての点を変化候補点と仮定するとwindowサイズの分計算量が増加してしまうので，最新の時刻を \(t\) として \(t-1\), \(t-2\), \(t-4\), \(t-8\),…をそれぞれ変化候補点と仮定して変化スコアを計算しました．こうすることで，右から入ってくる変化点に対して正確にスコアを計算できる一方で，計算量の増加をwindowサイズの \(\mathrm{log}\)オーダーに抑えることができます(図5)．

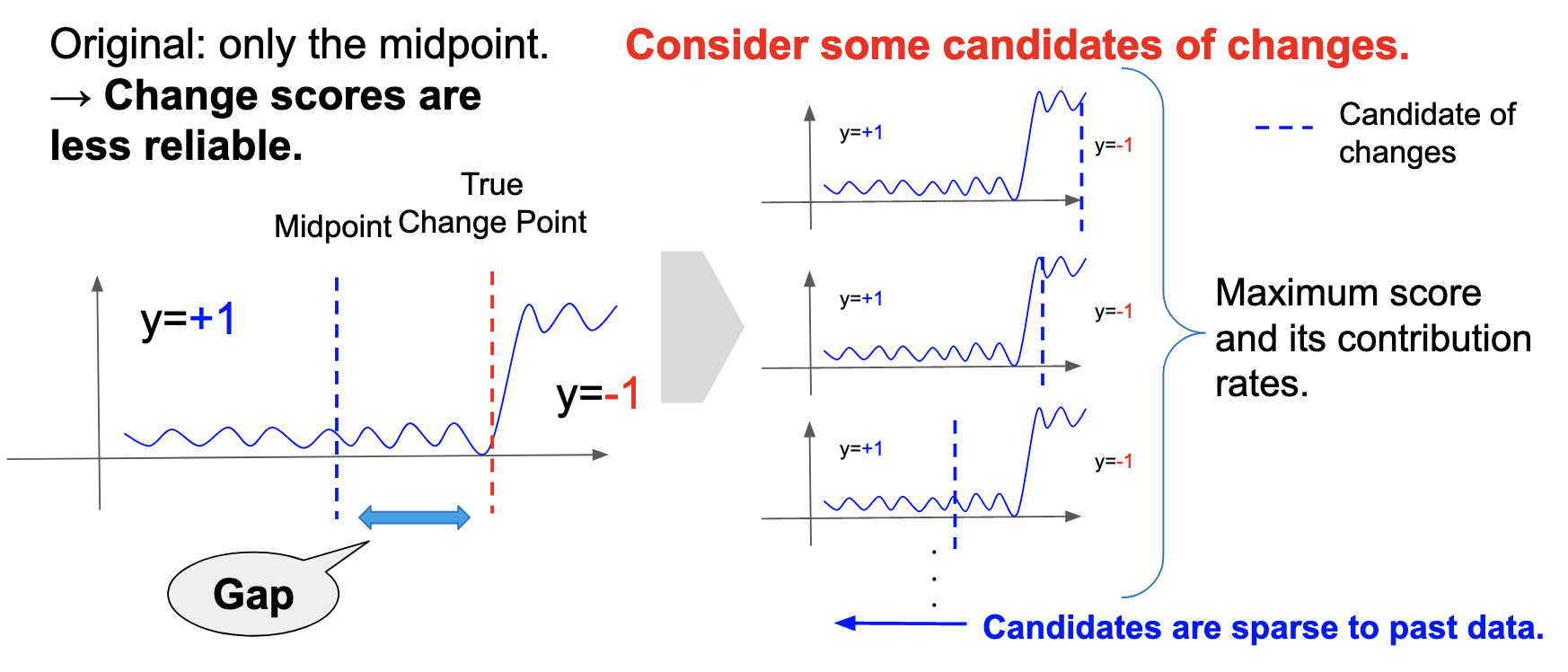
図5. アルゴリズムの改善の概念図．

改善点2. 漸進的変化に対応するaHSICの拡張

従来多くの変化検知では，突発的な変化の発生，つまり時系列データが従う確率分布の内部のパラメータがある時刻を境に一気に変わるタイプの変化が発生することが仮定されていました(Basseville and Nikiforov, 1993; Gralnik and Srivastava, 1999; Takeuchi and Yamanishi, 2006; Adams and MacKay, 2007; Saatçi, Turner, and Rasmussen, 2010)．これは主に統計学的な扱いがしやすいことに起因します．しかし，現実には漸進的に発生するタイプの変化，つまりある時刻の幅を持って確率分布のパラメータが徐々に変わるタイプの変化も発生しうると考えられます．漸進的変化ではパラメータがなだらかに変わるため，従来の突発的変化よりも検知が難しくなります．そこで，近年そのような漸進的変化(図6)およびその開始点をできるだけ早く検知しようとする研究が行われています(Yamanishi and Miyaguchi, 2016; Yamanishi et al., 2020)．

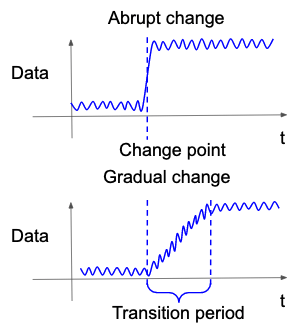
図6. 突発的変化と漸進的変化．

aHSICでも，暗に突発的変化の発生が仮定されています．そこで，これを漸進的変化の発生に対応するようように図7のように \(y\) を作り替えました．具体的には，原論文では変化点だと仮定されていた時刻を漸進的変化の開始点と考え，そこから \(y\) が一次関数にしたがって徐々に変わっていくように作り替えました．

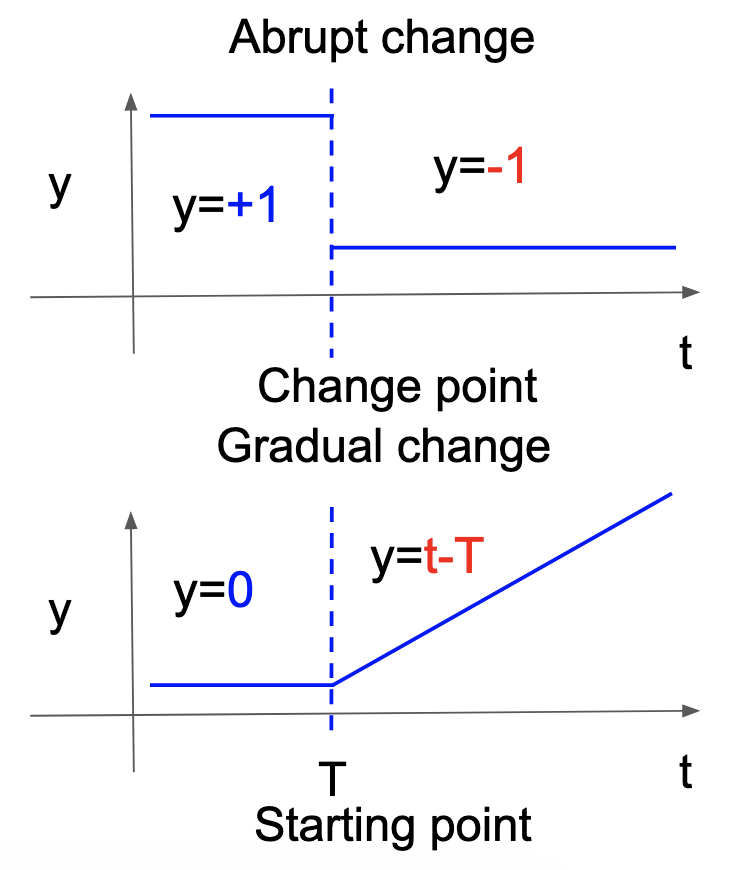
図7. 突発的変化と漸進的変化における \(y\) の作り替え．

改善点3. 正則化係数 \(\lambda\) の自動調整

本手法はいくつかのハイパーパラメータを持ちます．その中で，正則化の強さを決めるパラメータ \(\lambda\) は提案手法の性能を特に大きく左右します．では \(\lambda\) を調整するにはどうしたら良いでしょうか? 一つの方法としては，変化検知および変数同定の性能の定量的な評価指標を決め，与えられた時系列データおよび変化ラベルをvalidationとtestに分け，validationでパラメータをチューニング，testで性能を評価することが考えられます．しかし，変化点としてラベルが与えられていない点でも全く変化が起きていない，とは必ずしも保証できないケースも多々あり(例: ラベル作成時の変化の見逃し)，時系列データの負例ラベルの信頼性が少々下がります．そのため，ハイパーパラメータの変化ラベルに対する依存性が低い方が望ましいと考えられます．これを解決するために，式(1)の損失関数の第1項に対し，グリッドサーチとk-fold交差検証を用いて \(\lambda\) を決定する方法を提案します．このようにすることで，時系列データを利用しつつも，変化ラベルへの依存性を下げながら \(\lambda\) を決定することができます．

実験

以上3点の改善による性能を評価するために3つの実験を行いました．

評価指標

時系列データと，そのデータにおける真の変化点および変化が発生している変数が与えられている下で，変化検知と変数同定の性能を評価します．今，aHSICは1次元の変化スコアと多次元の変化の寄与度を出力しますが，変化検知はarea under the curve (AUC)で評価し，変数同定はmean average precision (MAP)で評価します．

AUC

AUCは2値分類において，正例と負例の割合が偏っているデータでの評価にも有効な評価指標です．通常，変化検知では異常データが正常データよりも圧倒的に少ないことが仮定されますので，評価に有効と考えられます．本実験では，真の変化点およびその付近のデータを正例，それ以外のデータを負例として扱い指標を計算しました(図8)．

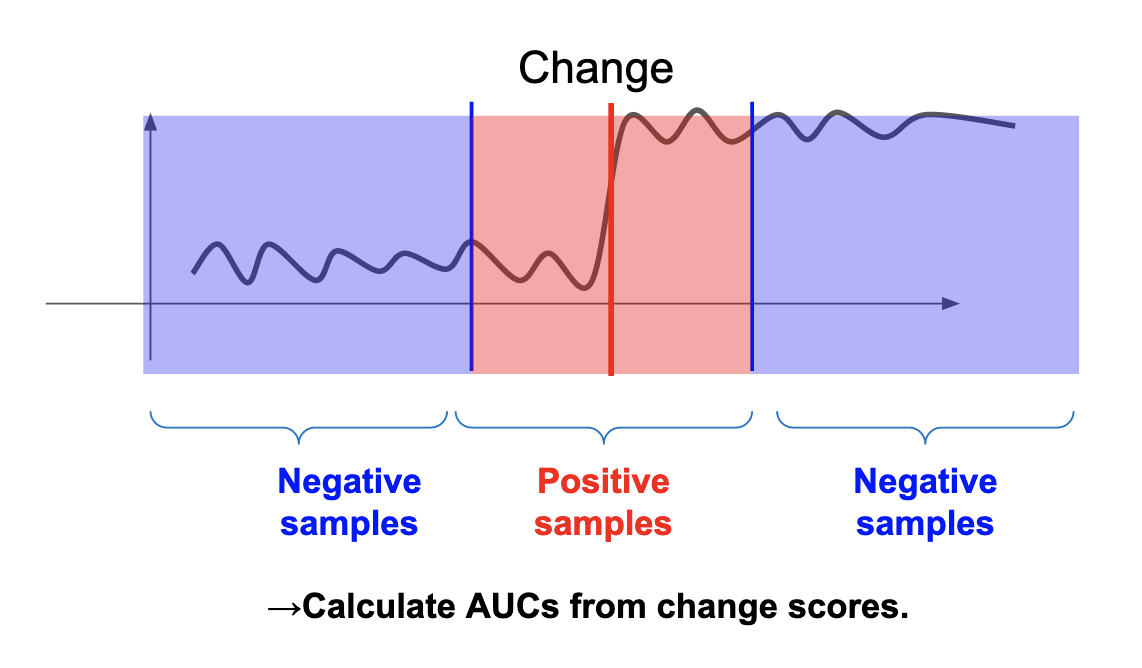
図8. AUC計算における正例と負例の設定方法．

MAP

次に，変数同定はMAPで評価しました．aHSICは各時刻において変化スコアと同時に変化への寄与度(contribution rate)を出力します．寄与度は高いほど，変化が起きている可能性が高いと考えることができるので，ランキング学習や物体検出で用いられる指標であるMAPを使うことができます(図9)．実験では，正例であるサンプルの寄与度のみ抜き出し，MAPを計算しました．

図9. MAPの計算方法．

生成した人工データ

以下に説明するungroupedデータとgroupedデータと呼ばれる2つのデータを作成しました．まず平均が0，分散が1の正規分布に独立に従う50次元，2000点のデータを生成し，そのデータを5次元ずつまとめ，10グループに分割します．次に，50次元の中から5次元を変化する次元として選ぶのですが，ungroupedデータではランダムに5グループ選び各グループから1つの次元を変化次元として選びました．一方groupedデータではランダムに1つのグループを選び，選ばれたグループの全ての次元を変化次元として選びました．そして，各変化では，平均を3だけ増加させました．最後に，データを等間隔に分割し9点の変化を生成しました．図10にデータの一例を示します．

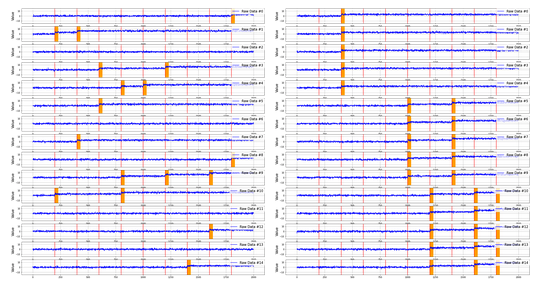
図10 ungroupedデータ(左)とgroupedデータ(右)の0から15次元目までを切り出したもの．赤線は変化が発生した時刻，オレンジの線は変化が発生している次元．

ただし，後述の実験2では改善点2の，漸進的変化に対しての拡張の評価を行います．そこで，平均を3増加させる際，突発的に増加させたデータと漸進的に増加させたデータの2種類を準備しました．漸進的変化では，transition periodの長さを30とし，平均を0から3に線形に変化させました．図11に一例を示します．

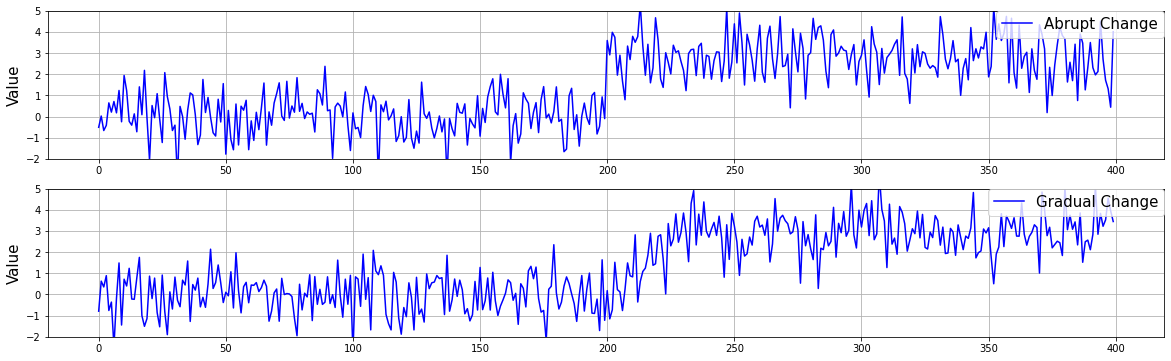
図11 突発的変化と漸進的変化の違い．

これらのデータをそれぞれ10本生成しました．生成したデータのパラメータを表1に示します．なお突発的変化の変化点および漸進的変化の開始点から30点をAUC・MAP計算のための正例に設定しました．

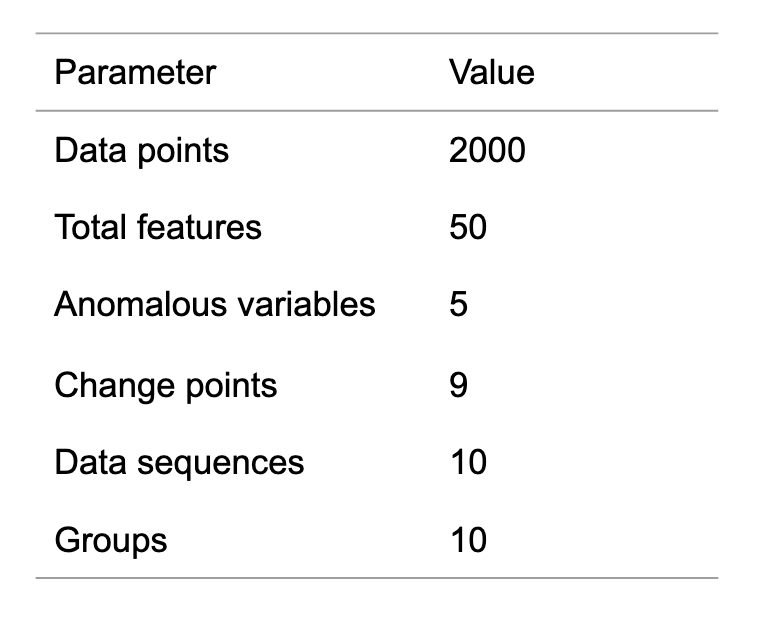
表1 生成したデータのパラメータ．

その他実験設定

手法の詳細

手法の詳細な設定について述べます．Lassoに基づくaHSIC，およびGroup Lassoに基づくaHSICの2つの性能を評価しました．Lassoの求解には座標降下法(coordinate descent method)を，Group Lassoの求解には近接勾配法(proximal gradient method)を用いました．
また，時系列データ \(X\) のグラム行列を計算するためのカーネルは全ての実験でradial basis functionカーネル(RBFカーネル)を用いました．\(y\) のグラム行列を計算するためのカーネルは，突発的変化の場合はデルタカーネル(入力の2つの変数が同じ場合に1を，それ以外の時に0をとるカーネル)を，漸進的変化の場合はRBFカーネルを用いました．
手法のもつハイパーパラメータはwindow幅・カーネルのバンド幅(\(X\) と \(y\) それぞれ)・正則化係数 \(\lambda\) が基本になります．ただし，突発的変化に関しては，デルタカーネルがバンド幅を持たないので，\(y\) のグラム行列を計算するためのバンド幅は必要ありません．
ハイパーパラメータは，生成した10本のデータのうち1つをvalidation, 残りの9本をtestに分け，次の節に示す方法で調整しました．

パラメータチューニング

変数同定の実運用を考えた時，変化と変数同定その両方が同時にうまく行われるべきであり，単体だけうまくいってもあまり意味がありません．そこで，Optuna(Akiba et al., 2019)のtree-structured Parzen estimator sampler (TPE, Bergstra et al., 2011)を用いてAUCとMAPの2変数最適化を行いました．そしてこの下で，パレート最適面を導出し，AUC+MAPを最適化するようなハイパーパラメータを採用しました(図12)．

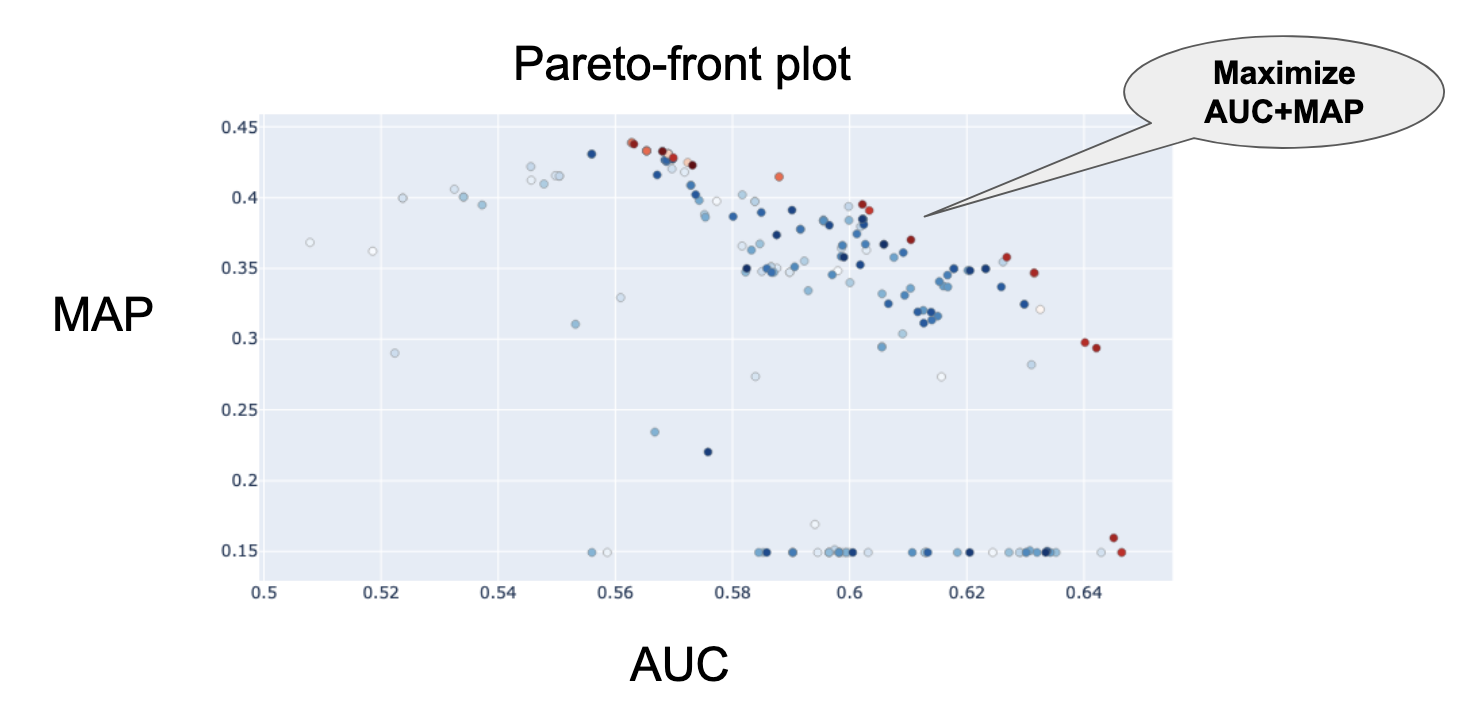
図12 AUCとMAPのパレート最適面．

以上の設定の下で，以下の3つの実験を行いました．なお，それぞれの実験では3つの改善点それぞれで，原論文のアルゴリズムよりどれだけ性能が改善したかを評価しています．そのため，改善点1と2を組み合わせるということなどはなく，いずれの実験も原論文と比較して単一の改善のみを施しています．

実験1: Window内の複数の点の探索による改善

ungroupedデータおよびgroupedデータに関して，LassoおよびGroup Lassoを適用しました．結果を表2に示します．ほとんどの場合において，提案方法でAUCおよびMAPを改善することがわかりました．また，groupedデータにLassoを適用した箇所でAUCの改善が確認できませんが，AUC+MAPの値を見ると改善していることが確認できます．

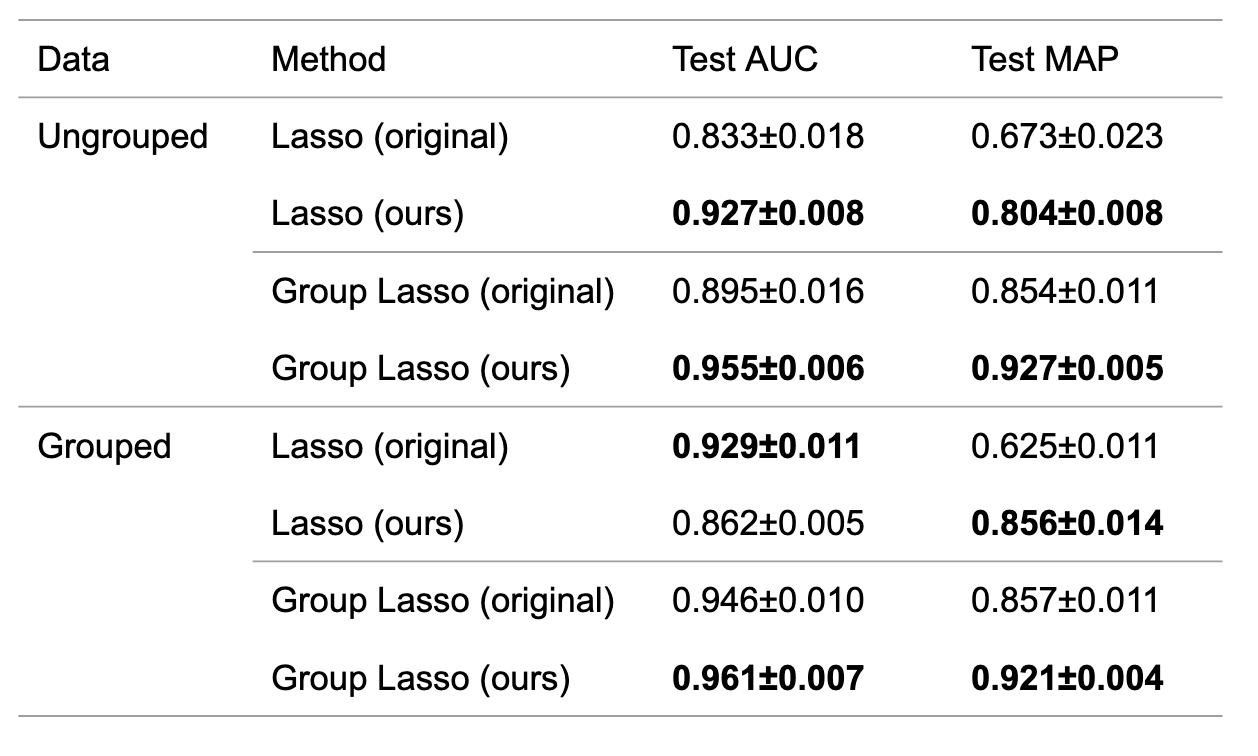
表2 原論文のアルゴリズムおよび提案アルゴリズムにおけるAUC・MAPの平均および分散．

実験2: 漸進的変化に対応するaHSICの拡張による改善

ungroupedおよびgroupedデータに関して，それぞれ突発的変化(abrupt)と漸進的変化(gradual)のデータ，計4種類のデータを生成しました．次に，LassoおよびGroup Lassoを適用しました．突発的変化および漸進的変化に対して手法を適用した結果を表3に示します．まず漸進的変化に関して結果を確認すると，概ね提案方法が原論文での結果を上回っていることが確認できました．さらに興味深いことに，突発的変化においても提案方法が原論文での結果を概ね上回っていることも確認できました．

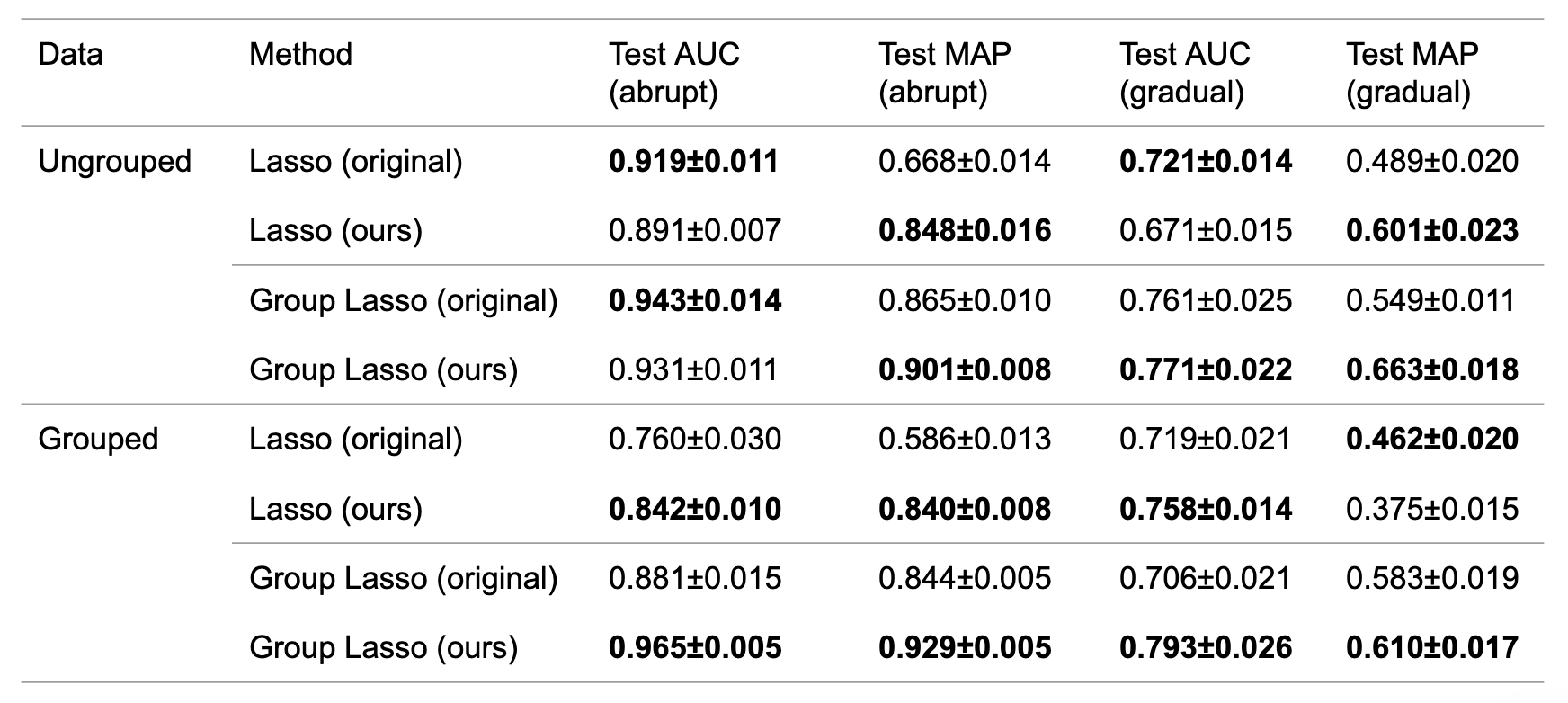
表3 原論文のアルゴリズムおよび提案アルゴリズムにおけるAUC・MAPの平均および分散．

実験3: 正則化係数 \(\lambda\) のCVを用いた調整による改善

ungroupedおよびgroupedデータに関して，LassoおよびGroup Lassoを適用しました．\(\lambda\) をcross validation (CV)を用いた調整をする場合，バンド幅・window幅をOptunaを用いて調整しました．一方 \(\lambda\) をCVを用いて調整しない場合，バンド幅・window幅・\(\lambda\) を
Optunaを用いて調整しました．(AUC + MAP の最大化をvalidationデータを使って行っていました)
結果を表4に示します．いずれの場合も，\(\lambda\) をCVを用いて調整するものは用いないものに匹敵する性能を出すことができています．そのため，性能を維持したまま，手法のハイパーパラメータに対する依存性を下げられていることがわかりました．

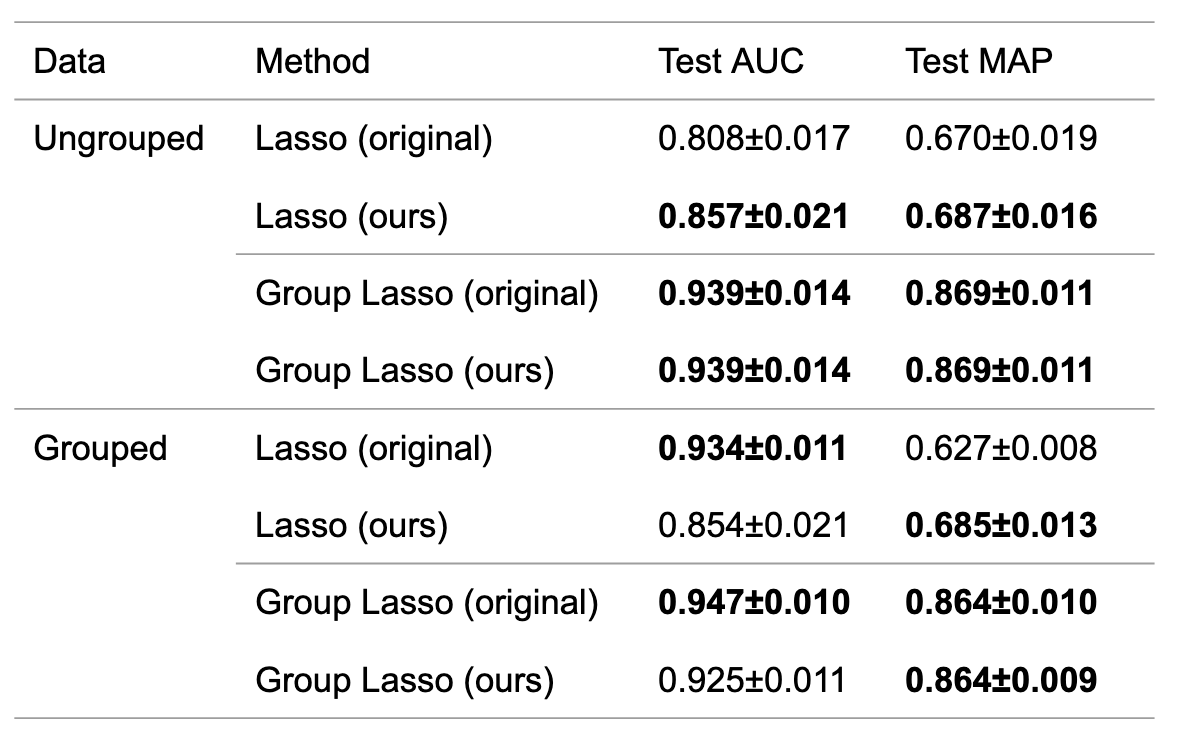
表4 原論文のアルゴリズムおよび提案アルゴリズムにおけるAUC・MAPの平均および分散．

まとめ

私はこのインターンシップでまず変化検知と変数同定について調査を行いました．そしてaHSICという手法に対し，window内の複数の点の探索・漸進的変化に対応するaHSICの拡張・正則化係数 \(\lambda\) の自動調整の3点の改善を施しました．前半2点では，AUCおよびMAPの改善が見られました．後半1点では，性能を保ちつつ，手法の異常ラベルに対する依存性を下げられることが確認できました．

将来的には下記の展開が考えられます．

・異常変数同定に関する性能解析
変化検知では，性能を評価するために誤検知・見逃しという指標があります．誤検知は変化がないにもかかわらずアラームをあげてしまうこと，見逃しは変化があるにもかかわらずそれを見逃すことを指します．そして，いくつかの論文(Basseville and Nikiforov 1993)でこれらの理論的な性能解析が行われています．しかしながら，今回の問題設定では，変化が発生している変数まで同定します．故に，変数同定に関する理論的な性能解析，選択された変数のデータ点数に関する一致性などを解析することが考えられます．

・ハイパーパラメータの自動調整
本記事では式(1)の第1項を最小化する方法で \(\lambda\) の自動調整を行う方法を紹介しました．実験的には良い結果が得られているものの，実は式(1)の第1項の最小化=AUCやMAPを最適化する，とまでは言えません．このあたりの関係性をよりクリアにする必要があります．
さらに，aHSICは他にウィンドウ幅とカーネルのバンド幅というパラメータを持ちます．ウィンドウ幅に関しては，適応的ウィンドウ(Bifet and Gavalda, 2007)というウィンドウサイズを可変にしながら変化検知を行う手法が提案されており，この手法と組み合わせることが考えられます．また，バンド幅に関してはカーネル法で一般的に存在するハイパーパラメータなので，一般的な調整方法を用いることができるでしょう．

・表3において確認された現象の解明
改善点の2つ目で，aHSICの漸進的変化への展開に取り組みました．漸進的変化に関する検知の性能が向上したのは良いとして，突発的変化に関しても性能が概ね向上するという興味深い結果が得られています．この原因の解明を行う必要があります．

謝辞

約1.5ヶ月間という限られた期間ではありましたが，社員の方のサポートのおかげで非常に充実したインターン生活を送ることできました．メンターの佐藤さん・森さんには特に手法についての議論や実装面でお世話になり，短期間で成果を出す上で大きな助けとなりました．ありがとうございました．同チームの小松さん・久米さんにはミーティングで貴重なコメントをいくつもいただけました．ありがとうございました．最後に本インターンシップで私が関わった全ての方に深く感謝し，お礼を申し上げます．