Blog
はじめに
この度PFN2025夏季インターンに参加させていただきました、東京大学大学院情報理工学系研究科修士1年の田代純也と申します。大学では、関節物体の3次元再構成に取り組んでいます。
今回のインターンでは、近年の3次元再構成分野の発展を支える根幹技術であるGaussian Splattingの改善に取り組みました。本ブログではその内容について紹介させていただきます。実験に使ったコードは https://github.com/pfnet-research/sketch-patch-init-relocate で公開しています。
背景
3次元再構成とは実世界の3次元的な形状や見た目をコンピュータ上で再現することであり、近年急速な発展を遂げています。PFNにおいても、PFN 3D Scanやバーチャルプロダクションのように3次元再構成技術を用いて多くのサービスが展開されています。

そして、現在この3次元再構成分野を支える根幹技術の1つが3D Gaussian Splatting (3DGS)[1]です。ここで扱うのはNovel View Synthesis (NVS)と呼ばれるタスクで、複数の視点からシーンを撮影した画像を用いて新しい視点から見た画像を合成するというものです。3DGSにおいては、3Dシーンを色や大きさを持った楕円球(Gaussian)の集まりとして表現し、微分可能なレンダリング過程により得られたレンダリング画像と正解画像の誤差に基づいてGaussianを更新(Backpropagation)することでこれを実現します。
しかし、このBackpropagationを用いたGaussianの最適化過程は非常に局所最適に落ちやすいことが知られています[2]。すでにこの問題の解決に取り組む研究は多くありますが[2, 3, 4, 5]、いずれの手法も一長一短な側面があり、万能と呼べるものはいまだに存在しません。そこで本インターンでは、それらの既存研究を踏まえつつ、3DGSの局所最適に落ちやすい問題を解消して再構成画像の見た目の品質を向上させることを目指します。
ただし本インターンでは、見た目の品質向上を目指すにあたって2つ制約を設けました。
- シーン表現に使用するプリミティブの数は増やさない
プリミティブ(3DGSの場合はGaussian)の数と見た目の品質の間には一般にある程度相関があるということが知られていますが[6]、Gaussianの数を増やすとレンダリングが遅くなる、学習・推論に必要なメモリ数が増えるといった別の問題が生じます。そのため、Gaussian数を増やすことで見た目の品質向上を図るのではなく、決められたリソースをいかに有効に利用するかという点にフォーカスを当てていくことにします。 - 推論パイプラインには変更を加えない
既に3DGSはメッシュや点群と並んでメジャーな3D表現方法のひとつになりつつあり、Blenderに代表される多くのソフトで3DGSを表示できるアドオンが存在します(PFNにおいてもUnreal Engine上で高速に3DGSのレンダリングが可能なプラグインを開発しています)。近年の3DGSから派生した研究においてはそもそも楕円球を用いた3Dシーン表現自体にテコ入れをしているものも存在しますが[7, 8]、これらの手法では推論パイプラインにも変更が加わり、3DGS用に開発されたビューワーなどをそのまま使用することはできずにやや汎用性に欠けるという側面もあります。これらはシーン内の高周波な成分を精度良く表現するためには有効なアプローチの1つではありますが、本インターンではあくまで3DGSにおける3Dシーンの表現方法そのものは変更せず、学習の過程を改善することで最終的に得られるシーンの品質を向上することを目指します。
関連研究
3DGS
3DGSの概要についてはすでに上で紹介させていただいた通りですが、ここではより詳細に説明を行います。
レンダリングの流れ
3DGSでは、3Dシーンを楕円球(Gaussian)の集合で表現します。各Gaussianは平均\(\mu \in \mathbb{R}^{3}\)、共分散行列\(\Sigma \in \mathbb{R}^{3 \times 3}\)、不透明度\(\alpha \in \mathbb{R}\)、色を表現するための球面調和関数の係数\(C \in \mathbb{R}^k\)という変数を保持しており、次のような広がりを持っています。
$$G(x)=e^{-\frac{1}{2}(x – \mu)^T \Sigma^{-1}(x – \mu)}$$
\(\Sigma\)は回転行列\(\mathbf{R}\)とスケーリング行列\(\mathbf{S}\)を用いて \(\Sigma = \mathbf{R}\mathbf{S}\mathbf{S}^T\mathbf{R}^T\) と表されます(実装上は\(\mathbf{R}\)はクォータニオン\(r \in \mathbb{R}^4\)、\(\mathbf{S}\)はスケール因子\(s \in \mathbb{R}^3\)で保持)。
以上のようなパラメータで表現されるGaussianは、レンダリング時にはまず画像平面に投影され、その後の式でブレンディングされます。
$$c(p)=\sum_{i=1}^Nc_i \alpha_i \prod_{j=1}^{i-1}(1- \alpha_j)$$
ここで, \(c(p)\)はピクセルにおけるRGB値です。ピクセル\(p\)をカバーするGaussianの集合を\(\{G_i | i=1,…,N\}\)とし、\(\alpha_i\)は\(G_i\)の不透明度にガウス分布の値\(G_i(x)=e^{-\frac{1}{2}(x – \mu)^T \Sigma^{-1}(x – \mu)}\)をかけたもので、\(c_i\)は球面調和関数より計算した\(G_i\)の色を表します。
学習
上で説明したレンダリングの過程は微分可能であるため、単純にレンダリング画像と正解画像の誤差を計算して誤差逆伝播法を適用することで色や位置などの各Gaussianの値を最適化できます。
しかし、前述の通り単純な誤差逆伝播法のみを用いた最適化では局所最適に陥りやすく、何らかの工夫が必要となります。そこで論文[1]では「SfM点群を用いた初期化」と「ADC(Adaptive Density Control)」という2つが最適化のパイプラインに組み込まれています。以下、それぞれについて説明します。
まずは1つ目の「SfM点群を用いた初期化」についてです。通常NVSのタスクを解こうとすると、各画像に対して「その画像がシーン中のどの位置から撮られたものか」というカメラパラメータを事前に推定しておく必要があります。多くの場合はSfM(Structure from Motion)と呼ばれる手法が用いられますが、SfMを用いたカメラパラメータの推定においては合わせてシーンの疎点群も得ることができます。そこで、現在一般的に用いられている3DGSにおいては、この疎点群を用いてGaussianを初期化しそこから最適化を始めます。
次に2つ目の「ADC」についてです。上で説明したSfM点群は非常に疎でシーンを写実的に表現するためにはプリミティブの数が不足しているため、最適化の最中に適切にGaussianをシーンに追加していく必要があります。論文[1]では、Gaussianが追加されるべき領域は「空白が生じている領域(under-reconstruction)」と「1つのGaussianが大きなエリアをカバーしている領域(over-reconstruction)」に大別され、いずれにおいても学習時にその領域にあるGaussianの位置に伝播する勾配が大きいと述べられています。前者に対してはcloneという処理が行われ、対象のGaussianと同サイズのGaussianが近くに追加されます。後者に対してはsplitという処理が行われ、対象のGaussianが2つの小さなGaussianに分割されます。さらに、Gaussianを増やすだけでなく、不要なGaussianを減らすpruningという処理も行われます。具体的には、不透明度が一定以下のGaussianはレンダリングに寄与していないとみなし、シーンから削除します。
課題
以上の工夫により3DGSは従来のNeRF等のニューラルネットワークベースの手法と同等以上のレンダリング品質を達成していますが、以下の課題が存在します。
- SfMによる初期点群は非常に疎であり最適解から離れていること
- ADCは多くのハイパーパラメータを慎重に調整する必要がありエンジニアリングへの依存度が高いこと
EDGS
次に、3DGSの初期化部分を改善したEDGS[3]について紹介します。この手法では、RoMa[9]というモダンな画像間マッチングモデルを用いて画像ペアから対応するピクセルを抽出し、三角測量により3次元空間中に点を追加するという操作を各画像ペアに対して行います。そして次にそのようにして得られた密点群を初期点群とし、3DGSを学習させます。このとき、ADCに関してはsplitとcloneは行われず、不透明度が一定値を下回ったGaussianを削除するpruningのみが行われます。
以上のように密点群を初期値とした3DGSの学習は非常に有効なアプローチの1つである一方、上の操作により得られた初期点群ではシーンの中の「たくさん見られている領域」に点が集まりやすくなり、撮影された回数が少ない領域は相対的に点が疎になってしまうという問題があります。また、Gaussian数の制御は完全にpruning頼りであり、最終的に得られるシーンのGaussian数を明示的に指定することができないという問題もあります。
MCMC
次に、3DGS-MCMC[4]について紹介します。この研究では、マルコフ連鎖モンテカルロ法の考えに則って3DGSの最適化に関する枠組みの改善が図られています。具体的には、最適化の最中にGaussianの位置に対して摂動が加えられることで、従来の3DGSに比べて局所最適に陥りにくくなり、再構成品質が向上したと報告されています。さらに、ADC部分にも改善が加えられており、従来のADCではシーンにGaussianを追加するsplit/cloneとシーンからGaussianを削除するpruningは完全に独立した操作でしたが、これがrelocationという一つの操作に統一されています。具体的には不透明度が一定値を下回ってpruningの対象となったGaussianを、不透明度が高い別のGaussianのそばに再配置するというものです。(より具体的には、各Gaussianに自身の不透明度に比例する確率を与えることで再配置先を確率的にサンプリングします)。
この手法により従来の3DGSに比べてGaussian数のコントロールが容易になった一方、不透明度が高いGaussianの近くにGaussianを再配置するという戦略でも同様にシーンの中の「たくさん見られている領域」ばかりにGaussianが集中してしまう問題が生じうるとも考えられます。訓練画像に多く含まれているような領域は早く最適化が進み不透明度が高くなることで、再配置先として選択されやすくなるためです。
手法
以上を踏まえ、本インターンでは3DGSの最適化パイプラインの改善を試みました。以下の図は提案手法の全体像です。大きく2つの要素からなります。
- RoMaを用いて密点群を得たのち訓練ビューの偏りを考慮してサブサンプリングする「初期化」
- 不透明度が高いところではなくレンダリング画像の誤差への影響が大きいところを積極的に補填する「再配置」
1. 初期化
EDGSではRoMaにより得られた密点群をそのまま初期点群として使用し、最適化中のpruningによってGaussian数が決定していました。しかしここでは、あらかじめ決められたGaussian数の中で最適化を行うため、初期点群の段階で所望の点数に削減しておくことを考えます。得られた密点群をサブサンプリングする方法として、最もナイーブには全ての点に一様な確率を与えランダムに点を減らすことが考えられます。この場合、サブサンプリング前後で点群の密度分布は保たれますが、前述の通りRoMaによる点群の獲得においては訓練ビューにたくさん含まれている領域に点が多く集まるため、得られる点群の密度分布は撮影データに大きく依存します。
そこで本インターンでは、多くの訓練ビューに含まれている領域については過剰に撮影されたことにより点が増えているとみなして積極的に点を減らし、そうでないような領域はあまり点を減らさないことで訓練ビューの偏りを排除する「view-balancedサブサンプリング」を提案します。
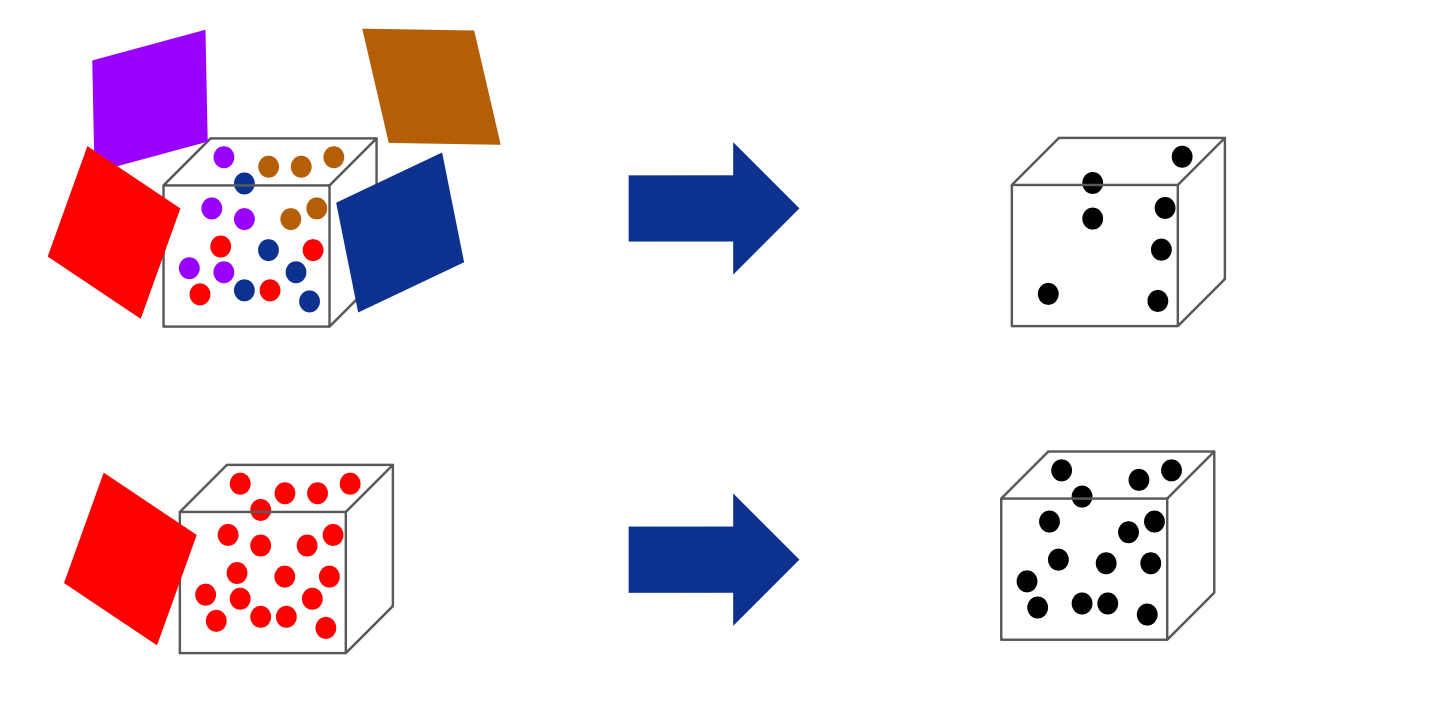
これを実現するためには「ある領域がどれくらい多くのビューから見られているか」という偏りを考慮して各点にサンプリング確率を与える必要があります。ここでは、各点がどのビューから得られた点かという情報を保持しておき、それを小さいボクセルごとに集計することで確率を計算するという方法を取りました。具体的にはあるボクセル\(v\)について、その中にビュー\(i (i=1,…,n)\)から得られた点が\(N_{v,i}\)個ずつ存在するとしたとき、ボクセル\(v\)内の点は全て以下の確率\(p_v\)で選択されます。
$$p_v=k \frac{\max_{i=1,…,n} N_{v,i}}{\sum_{i=1}^nN_{v,i}}$$
(\(k\)はサブサンプリング前後の点の数により決定する比例定数) 多くのビュー由来の点が入り混じっているようなボクセルについては\(p\)が小さくなることで積極的に点が減らされ、逆に特定のビュー由来の点が多数派を占めるようなボクセルについては\(p\)は大きな値を取り、点はあまり減らされません。以上のview-balancedサンプリング手法の導入により、シーン中の「訓練ビューにおいてあまり見られていない」ような領域についても精度良く再構成されることが期待されます。
2. 再配置
3DGS-MCMCにおいては不透明度が低いGaussianを不透明度が高いGaussianのそばに再配置するという「relocation」が行われていました。しかしこの方法では、頻繁に見られているGaussianは最適化が進み不透明度が高くなるため積極的に補填されるものの、そうでないようなGaussianはたとえ表現力が不足していて本来Gaussianが追加されるべき領域であっても補填が行われません。
そこでここでは、不透明度が高いところではなくレンダリング画像の誤差への影響が大きいと思われるところを積極的に補填するようなrelocationを提案します。relocationにおいては「再配置対象」のGaussianと「再配置先」のGaussianを決める必要がありますが、提案手法ではこのうち前者は従来のものをそのまま使用し、後者を変更します。具体的には、3DGS-MCMCでは不透明度に比例する確率に基づいて再配置先を決定していたものの、本手法では従来のADCにならってGaussianの位置に伝播する勾配が大きいところを再配置先として選びます。
実験・考察
実験1
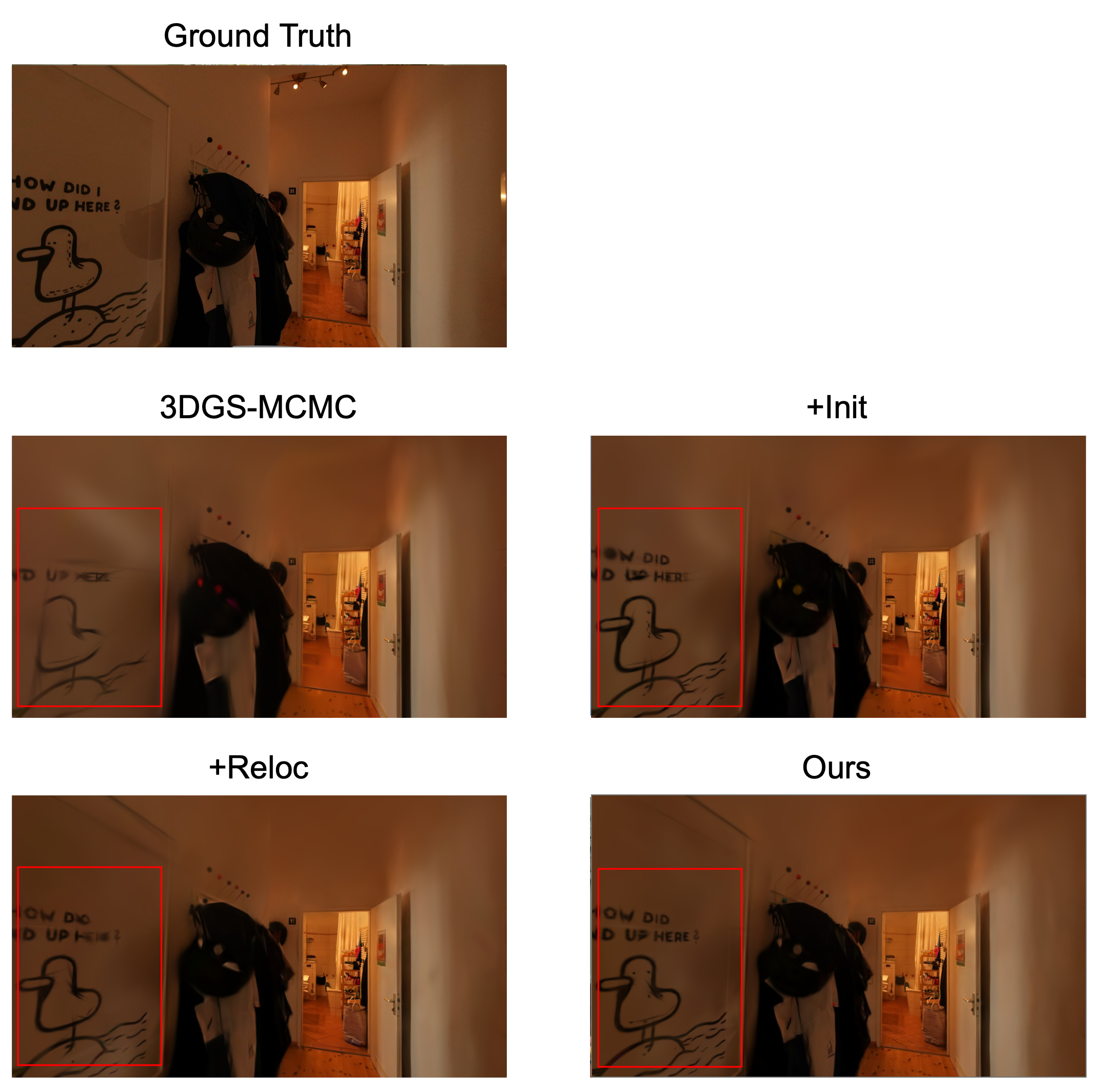
以上の手法が既存のベースラインに対して有効であるかを検証するため、実験を実施しました。実験にはZip-NeRFデータセット[10]を使用しました。このデータセットは一部屋外のシーンも含んだ4つのシーンからなり、NVSのタスクで広く用いられているデータセットに比べてシーンが広くより現実的な問題設定に近いという特徴があります。また、評価指標にはPSNR、SSIM、LPIPSの3つを使用しました。3DGS-MCMCをベースラインとし、上で提案した2つの手法の有無による結果の差を比較した結果を以下に示します(AlamedaやBerlinはシーンの名前です)。表は上から順に3DGS-MCMCの結果、初期化のみを適用した結果、再配置のみを適用した結果、両方を適用した結果です。
いずれのシーンにおいても、2つの提案手法を両方とも導入した場合の再構成結果が最も良い性能を発揮していることが分かります。また、定性評価においても窓の外や壁・床の模様といった細部の表現において特に提案手法が優れていることが分かります。
| PSNR ↑ | alameda | berlin | london | nyc | mean |
|---|---|---|---|---|---|
| 3DGS-MCMC | 22.64 | 26.09 | 25.83 | 26.48 | 25.26 |
| +Init | 22.79 | 26.91 | 26.27 | 27.35 | 25.83 |
| +Reloc | 22.77 | 26.82 | 26.63 | 27.23 | 25.86 |
| Ours | 22.83 | 27.43 | 26.80 | 27.56 | 26.15 |
| SSIM ↑ | alameda | berlin | london | nyc | mean |
|---|---|---|---|---|---|
| 3DGS-MCMC | 0.7707 | 0.8759 | 0.8223 | 0.8456 | 0.8286 |
| +Init | 0.7774 | 0.8943 | 0.8359 | 0.8657 | 0.8433 |
| +Reloc | 0.7839 | 0.8923 | 0.8464 | 0.8680 | 0.8476 |
| Ours | 0.7883 | 0.9030 | 0.8516 | 0.8754 | 0.8546 |
| LPIPS ↓ | alameda | berlin | london | nyc | mean |
|---|---|---|---|---|---|
| 3DGS-MCMC | 0.2690 | 0.2545 | 0.2690 | 0.2135 | 0.2515 |
| +Init | 0.2582 | 0.2162 | 0.2423 | 0.1774 | 0.2235 |
| +Reloc | 0.2355 | 0.2155 | 0.2148 | 0.1653 | 0.2078 |
| Ours | 0.2283 | 0.1889 | 0.2052 | 0.1503 | 0.1932 |


実験2
続いて、初期化におけるサブサンプリング手法に関する比較実験を行いました。すでに上で説明したview-balancedサブサンプリング以外に以下の3つと比較しました。
- randomサブサンプリング: 各点を一様確率で選択し、サンプリング前後の密度分布が等しくなるようにサンプリングする。
- voxelサブサンプリング: 空間をボクセルで分割し、各ボクセル中の点の数が等しくなるようにサンプリングする。
- frequency-awareサブサンプリング: 高周波な領域は密に、低周波な領域は疎になるようにサンプリングする。具体的には、画像上でラプラシアンフィルタをかけた値に応じて各点に確率を与える。
また、view-balancedサブサンプリングは「シーンの中のあまり見られていない領域も良い精度で再構成する」ことを目標としているため、評価指標についても慎重に考える必要があります。というのも、NVSタスクにおいては全画像の8枚に1枚をテスト画像することが多いのですが、これでは訓練画像とテスト画像が似通った分布になるため結局は「たくさん見られている領域を重点的に補強する」ような手法が優れた数値を得ることになります。そこで本実験では、テスト画像のスコアが悪かった10%枚での平均値も算出することで、簡易的に「あまり見られていない領域」に対する再構成精度を確認しています。結果を以下に示します(スコアは4シーンの平均値です)。
全体平均としては、若干ですがview-balancedがrandomを上回っており、さらに下位10%においてはその差はより顕著になっています。このことから、view-balancedサブサンプリングの狙い通り、シーン全体をバランスよく再構成できているのではないかと考えられます。
一方で、voxel、frequency-awareの2つについては、特にLPIPSなどにおいては上2つに比べると劣る結果となりました。この原因について、voxelの場合はシーンのいかなる場所でも一様な密度に近づくようにサンプリングされるため、一般に多くのGaussianが必要になる高周波領域に点が集まらなかったのではないかということが仮説として考えられます。逆にfrequency-awareの方ではラプラシアンフィルタの特性上エッジ付近のみに点が集中し、カーペットのようなエッジ以外の高周波寄りの領域に点が集まらなかったのではないかと考えられます。
| PSNR ↑ | SSIM ↑ | LPIPS↓ | PSNR worst 10% ↑ |
SSIM worst 10% ↑ |
LPIPS worst 10% ↑ |
|
|---|---|---|---|---|---|---|
| view-balanced | 26.15 | 0.8546 | 0.1932 | 20.62 | 0.7248 | 0.3359 |
| random | 26.13 | 0.8541 | 0.1936 | 20.56 | 0.7216 | 0.3419 |
| voxel | 25.91 | 0.8434 | 0.2163 | 20.70 | 0.7105 | 0.3687 |
| frequency-aware | 26.06 | 0.8480 | 0.2078 | 20.52 | 0.7148 | 0.3617 |
おわりに
本インターンでは、3DGSの最適化に「ビューの偏りを考慮した初期化」と「再構成誤差が大きいところへのGaussianの再配置」を組み込むことでレンダリング画像の品質が向上することを確認できました。一方で、今後の課題については以下が挙げられます。
- より明示的な初期点群の分布制御: view-balancedサブサンプリングはビューの偏りは補正するもののあくまでも「RoMaの処理でどのような点がマッチングされるか」に依存して密度分布が決まります。結果として今回の手法ではRoMaにより得られた点群分布に依存する形で初期点群を獲得するのが最も良い結果となりましたが、freqency-awareサブサンプリングなどのようにサンプリング前の点群分布に依存しないような手法を見つけることができれば、LiDARなど任意の方法で得られた密点群を使用することができます。
- より適切な「誤差スコア」の計算: 今回の手法ではADCにならい、学習中の位置の勾配が大きいGaussianは誤差への影響が大きいため補強が必要である、と考えました。しかし、実際には局所最適に陥ったGaussianはたとえ誤差が大きく補強が必要であっても勾配は0に近いため、この方法では補強の対象には選ばれません。各Gaussianに対して「どれくらい補強が必要か」を表現するより良い指標の探索も、今後の課題として考えられます。
最後になりましたが、7週間お世話になったメンターの小林さん、菊池さんのお二人をはじめとするPFNの皆様に心から感謝申し上げます。論文を読む時の心構え、抽象的な議論から実装のアイデアに至るまでのスピード感など、日々の議論を通して勉強になることばかりでした。ありがとうございました。
参考文献
- Kerbl, Bernhard, et al. “3D Gaussian splatting for real-time radiance field rendering.” ACM Trans. Graph. 42.4 (2023): 139-1.
- Yang, Haosen, et al. “Improving Gaussian Splatting with Localized Points Management.” Proceedings of the Computer Vision and Pattern Recognition Conference. 2025.
- Kotovenko, Dmytro, Olga Grebenkova, and Björn Ommer. “EDGS: Eliminating Densification for Efficient Convergence of 3DGS.” arXiv preprint arXiv:2504.13204 (2025).
- Kheradmand, Shakiba, et al. “3d gaussian splatting as markov chain monte carlo.” Advances in Neural Information Processing Systems 37 (2024): 80965-80986.
- Rota Bulò, Samuel, Lorenzo Porzi, and Peter Kontschieder. “Revising densification in gaussian splatting.” European Conference on Computer Vision. Cham: Springer Nature Switzerland, 2024.
- Shi, Yuang, et al. “Sketch and Patch: Efficient 3D Gaussian representation for man-made scenes.” Proceedings of the 17th International Workshop on IMmersive Mixed and Virtual Environment Systems. 2025.
- Liu, Rong, et al. “Deformable beta splatting.” Proceedings of the Special Interest Group on Computer Graphics and Interactive Techniques Conference Conference Papers. 2025.
- Ye, Zhifan, et al. “3D Gaussian rendering can be sparser: Efficient rendering via learned fragment pruning.” Advances in Neural Information Processing Systems 37 (2024): 5850-5869.
- Edstedt, Johan, et al. “Roma: Robust dense feature matching.” Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2024.
- Barron, Jonathan T., et al. “Zip-nerf: Anti-aliased grid-based neural radiance fields.” Proceedings of the IEEE/CVF International Conference on Computer Vision. 2023.
Area