Blog

私がPFNに入ってから知った、もっとも好きな技術トピックの一つである、MN-Core™向け再計算のご紹介をします。再計算(recomputation、rematerializationやcheckpointingなどのキーワードで呼ばれることもあります)は、その名の通り同じ計算を複数回することで、GPUメモリを節約するために再計算を利用するテクニックは広く知られています。PFNでも、再計算を使ったメモリ節約アルゴリズムに取り組み、実際の事業でフル活用しています。
MN-Core向けの再計算は、消費メモリ削減でなく、高速化を主目的としています。再計算で計算する量が増えるにも関わらず、高速化が達成できるというのが、私がとても面白いと思う点です。カラクリを紹介していきます。
MN-Coreは、DRAMとSRAMの二種類のメモリを持ち、使えるリソースをとにかく演算器に費やしているのが特徴のアクセラレータです。演算器がたくさんあることと、最高級DRAMを使っていないことから、主記憶のバンド幅と演算性能の比を示すB/F比が極端に低い設計になっています。高B/F比を指向した富岳とは、対照的な設計です。一般的に、B/F比は高ければ良いというものではないものの、高い方が使いやすいとされていて、B/F比の低いアクセラレータをうまく使いこなし、一方でエンドユーザには使いにくさを見せない、というのはかなりチャレンジングな課題で、ソフトウェアエンジニアとしては、頑張りどころであると考えています。なにしろ、うまく使いこなせば、とんでもない性能が出るのです。
その前提で、具体的な深層学習の計算を考えてみます。
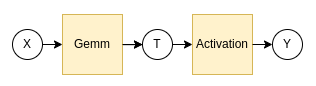
図1: 典型的な深層学習の計算グラフの一部
図1のような、深層学習モデルの計算の一部を切り出したものを例として考えます。XからTが作られ、TからYが作られる、というようなシンプルな例で、この計算中はX,T,YをMN-CoreのSRAMに保持できる、という前提で考えます。このような計算は、MN-Coreがそのありあまる演算器をいかんなく発揮できるため、非常に高速に実行することができます。
深層学習では、多くの場合、誤差逆伝播(backpropagation)のための計算がセットでついてきます。図1に対する逆伝播の計算を図2で示します。
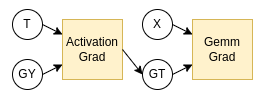
図2: 図1に対応する誤差逆伝播の計算グラフ
ここで、GY,GTはY,T,Xと同じサイズなので、SRAMに保持できるのですが、XとTはSRAMに保持し続けられるとは限りません。図1は深層学習モデルの一部を切り出したものであったため、Yを計算した後、モデルの他の部分の計算をしている間に使用しないX,Tを保持し続けるのは不可能な場合が多いからです。なので、XとTをDRAMに置くことを考えると、全体のグラフは図3のようなものになります。
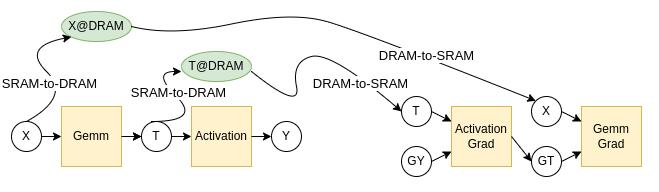
図3: SRAM⇔DRAMの移動を加えた計算手順
これで、実行可能な計算手順となりました。しかし、前述の通り、MN-CoreのB/F比は非常に低いため、このような計算を実行すると、SRAMとDRAMの間のコピーが律速し、演算器が遊ぶ状況になってしまいます。ここで再計算の登場となります。再計算を利用した計算手順例が図4となります。
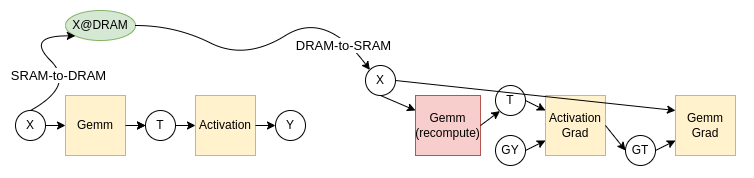
図4: SRAM⇔DRAMの移動を再計算で置き換えた計算手順
仮に、SRAM-to-DRAMとDRAM-to-SRAMのコストを3、GemmとGemmGradのコストを2、ActivationとActivationGradのコストを1とすると、再計算をしない図3はコスト18、再計算を利用した図4はコスト14となるので、高速化に成功した、ということになります。MN-CoreのB/F比だと、DRAM-to-SRAM(T)をやっている間にGemmを6回できる、というような場合も珍しくないので、SRAMとDRAM間のコピーを再計算によって削減するのは、非常に重要なテクニックとなっています。表1に、とあるCNNモデルとGNNモデルで再計算を使ってスケジュールした場合としない場合の性能差を示しています。かなり効果の大きい最適化であることがわかります。
| モデル | 再計算なし | 再計算あり | 性能向上率 |
| CNN | 30.504 msec | 20.847 msec | 46% |
| GNN | 18.127 msec | 15.882 msec | 14% |
余談ですが、PFN社内では、SRAM-to-DRAMのコピーを「アップロード」、DRAM-to-SRAMのコピーを「ダウンロード」と呼んでいます。コピーにかかる時間が相対的に大きいことと、MN-Coreが画像処理をする深層学習モデルをターゲットにデザインされていることをうまくとらえていて、社内で愛されているスラングとなっています。
今回示した例はとてもシンプルでしたが、普段我々が扱っている計算グラフは、10000程度のノードがあり、かつ複雑に分岐しているようなものになっています。さらに話をややこしくすることとして、MN-CoreのSRAMは複数種類あり、また、Gemmなどの計算カーネル実装も「SRAMを潤沢に使うが高速なモード」と「少し遅いがSRAM消費が少ないモード」「入力をinplaceで書き変えて出力とするモード」などというように複数種類準備できるということがあります。また、DRAMへのコピーと計算カーネルの実行は、同時に行なえる場合があることも考慮しなければなりません。我々の再計算スケジューラは
- 計算順序を工夫して、SRAMにある値をなるべく再利用する
- 再計算を挿入し、DRAMへのコピーを抑える
- SRAM消費と速度のトレードオフを考慮して、適切な計算カーネル実装を選択する
- DRAMへのアクセスを分散し、計算中にコピーできるようにする
と、かなりややこしい組合せ最適化問題を解くことになります。現在では、それなりに満足のできる実装ができているものの、まだまだ最適でないと考えられ、また、収束が非常に遅く、ワークロードによっては20時間以上かけて最適化しているようなケースさえあります。ですので、アルゴリズムが得意な人々はぜひ、入社し、圧倒的改善をなしとげていただきたい、というようなことを思っています。PFNではMN-CoreやGPU向けのコンパイラエンジニアを募集しています!
とにかく演算器をたくさん乗せ、バンド幅律速でない計算は超高速にこなせるようにしつつ、バンド幅が必要になる計算は足りないバンド幅を再計算で補って適用可能範囲を広げる、というMN-Coreの思想は、最初に理解した時は「なるほどー」と思ったものでした。
歴史的には、多少のゆり戻しが時々あるものの、プロセッサのB/F比は時とともに低くなっています。このトレンドがまだまだ続くのであれば、主記憶のバンド幅というのは、演算器の性能に比して、どんどん貴重なものとなっていきます。演算器の性能によってバンド幅を「買う」ことができる再計算技術は、今後もより重要性が増していくかもしれません。
今回紹介したような大域的な計算順序の変更を伴う最適化は、GCC/Clangのような、古典的なコンパイラでは実現が非常に困難なものでした(注1)。深層学習では、ユーザがtorchやnumpyなどのインターフェイスを使って、抽象度の高い記述をしているため、古典的なコンパイラではなかなか実現できなかった、計算全体を見渡した大域的な最適化を行なうことができる、というところが非常に面白いところだと思っています。もう一つ、古典的なコンパイラではやりづらかった大域的な最適化として、ユーザのデータを計算の都合で勝手に並び変えるというものがあります。この話は以前したこともあるのですが、次回以降のブログで、あらためてご紹介します。
注1: 再計算自体は、たとえばこの論文やこの論文のように古典的なコンパイラでレジスタ割り当て問題に関連して研究されてきましたが、基本的には局所的な最適化であると理解しています。