Blog
(読んでいただいた方からの指摘を受けて訂正しました.またtwitterでも感想や指摘を頂きました.ありがとうございます.)
はじめに
こんにちは,大野(@delta2323_)です.今日はルベーグの収束定理についてお話をしたいと思います.
物理や応用数学の分野では極限を直感的に扱って,ざっくりと計算を進める事があります.しかし,気をつけないと実は正当化できないという計算を無意識のうちにおこなってしまいかねません.一方,そのような罠にはまった事がある人が,式変形の度に直感的な議論が正しいかに気を揉み,計算がなかなか進まないのも問題です.
では,数学に近い人が極限の定義に戻って式の妥当性を逐一詳しく検証しているかというとそうではありません.確かに,極限の厳密な定義は\(\epsilon – \delta\)論法を用いて行われ,「わからなくなったら\(\epsilon – \delta\)にもどれば証明できるだろう」と考える事が多いと思います(プログラマーが分からなくなったらソースを読むように!).しかし,そこまで細かい事を考えなくても,ルベーグ積分論の中には,比較的簡単な条件をチェックする事で極限と和や極限と積分を交換する方法,つまり,直感的な式変形を正当化する為の簡便な手続きがあります.今回はそれを紹介しようと思います.
本当はルベーグ積分を勉強してその定理の証明を追うのが本筋だと思います(個人的にはその定理の証明を追うためにルベーグ積分論を勉強してもよいくらいだと思っています).しかし今回はブログのエントリーですので,手軽に扱えるように定理を少し書き変えて紹介したいと思います.
以降扱う主要な定理は基本的に結論の式は全て同じで,次のような形をしています.
\(\displaystyle{ \lim_{n \to \infty} \int_{I} f_{n}(x)dx = \int_{I} \lim_{n \to \infty} f_{n}(x)dx}. \)
この式に現れる\(I\)や\(f_{n}\)や\(f\)が定理によってどのように異なるかに注目して議論を追ってみてください.
関数の値域についての注意
今回の話では,関数の値域は\(\infty\)を含まないとします.例えば,\(f(x) = \frac{1}{x}\)と書いた場合,解釈は2通り考えられます.
- \(f\)の定義域は\(\mathbb{R} \setminus {0}\)で,\(x = 0\)では\(f\)は定義されていない
- \(f\)の定義域は\(\mathbb{R}\)全体で,\(f(0) = \infty\)とする
ルベーグ積分の一般論ではこのような例は同一視して扱う事が多いですが,今回のエントリーではこの2つを区別し,連続関数と言った場合には上のスタンスをとることにします.
一番安全な場合
和と積分が交換できなくなるような状況が起こるのは,何らかしらの点で無限が絡む場合です.まずはそのような面倒な状況が起こらない場合を考えてみます.
\(I = [a, b] (a \leq b)\) を数直線上の区間とします.例えば \([0, 2pi], [-pi, pi], [0, 1] \) などがこのような区間の例です.逆に\(I = \mathbb{R}, [0, \infty )\)等は最初は考えません.また,この段階では\([0, 4)\)や\((1, 3)\)のようなどちらかに開を含むような区間も考えません.それの種明かしは後述します.
この範疇でのルベーグの収束定理を述べてみます.
象徴的に\(f = \displaystyle{ \lim_{n to \infty} f_{n}}\)と書いたとすると,これを定理の結論の式に代入する事で,ちょうど積分と極限が両辺で交換された形の式ができあがります.
反例を作る
上の定理では,区間\(I\), 関数列\({f_{n} }_{n=1}^{\infty}\), 関数\(f\)それぞれについて条件がありました.これらの条件はどれを削っても収束しなくなる可能性があります.この節では上に挙げた定理について反例を作って実際に和と極限が交換できない場合がある事を確認してみます.もっと強い事が言える定理を知りたい場合は次の節まで飛んでください.
反例1:区間が有限ではない場合
まず\(I\)が有限な区間ではなく,無限の区間の時の反例を示します.つぎのような状況設定を考えます.
- \(I = [0, \infty). \)
- \(f_{n} (x) = \max ( \min(x – (n-1), -x + n), 0 ).\)
- \(f(x) = 0.\)
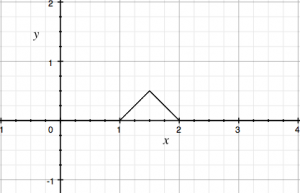
とします.\(f_{n}\)は式で書くと複雑ですが,例えば\(n=2\)の場合を図示すると,下図のようになります.
\(n\)を大きくすると,山が右に移動していきます.
\(f_{n}\)は連続関数で,\(f_{n}\)は\(f\)に各点収束します.すなわち,\(I\)が閉区間である事を除いて,定理の条件は満たされています.しかし,定理の結論が満たされていません.実際に試してみると,
- (左辺)\(\displaystyle{= \lim_{n to \infty} \int_{I} f_{n}(x)dx = \lim_{n to \infty} 1/4 = 1/4 .} \)
- (右辺)\(\displaystyle{= \int_{I} \lim_{n to \infty} f_{n}(x)dx = \int_{I} f(x)dx = \int_{I} 0 dx = 0 . } \)
のようになります.確かに反例となっています.
反例2:区間が閉区間でないとき
区間\(I\)が無限に飛んでしまうと,定理が成り立たない例を見つけました.今度は長さが有限だったとしても,閉区間でないと定理が成り立たないかもしれない事を確認します.
- \(I = (0, 1]. \)
- \(f_{n} (x) = \max(-n^{2}x +n, 0).\)
- \(f(x) = 0.\)
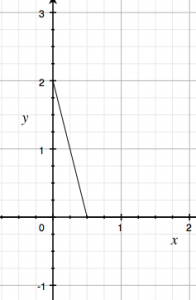
とします.図で書くと,\(n\)が増えるほど,\(y\)軸をのぼり上がって行くようなグラフになります.下図は\(n=2\)の場合での\(f_{n}\)です.
デルタ関数を,この\(f_{n}\)の極限として構成するという方法があります.しかし,今回の話では\(” f(0) = \infty”\)という物議をかもしそうな代物は避けて議論を進めます.具体的には定義域を\((0, 1]\)として,\(1/0\)という計算はしていません.
この条件設定でも,区間が閉区間である以外の定理の条件は満たしています.しかし,先ほどと同じように,
- (左辺)\(\displaystyle{= \lim_{n to \infty} \int_{I} f_{n}(x)dx = \lim_{n to \infty} 1 = 1,} \)
- (右辺)\(\displaystyle{= \int_{I} \lim_{n to \infty} f_{n}(x)dx = \int_{I} f(x)dx = \int_{I} 0 dx = 0 } \)
となり,両者は一致しません.
収束定理を拡張する
それでは,今述べた定理を拡張してみます.前のバージョンの収束定理では,\(I\)が有限の閉区間しか定理の対象になっていない点が扱いづらいです.例えば何かの量を全区間で積分するというのは良くある話なので,積分範囲として\((-\infty, \infty)\)のようなものがあってほしいです.また,今回の拡張で,先ほどは扱えなかった開を含むような区間もターゲットにできるので,今回の拡張に含みます.今回は積分範囲は次のような形を考えます
\(I = [a, b], (a, b), (a, b], [a, b), (-\infty, b], (-\infty, b), (a, \infty), [a, \infty), (-\infty, \infty) .\)
区間は無限に伸びている可能性がありますが,\(f(\infty)\)のような値は定義する必要はない点に気をつけてください.
もっと複雑な定義域を考える時には,有限個の区間に分けて各々で定理を適用すればよいです.無限個の区間にしか分ける事が出来ない場合は・・・今回は考えない事にします.
さて,この条件下でのルベーグの収束定理を述べてみます.
太字になっている部分が前のバージョンの定理と異なる部分です.
この定理が何を主張しているか?
まず定理が主張している事を理解しましょう.一つ目の主張は,\(f\)が可積分である事,つまり\(f\)の絶対値を取って積分を取ると有限になる事です.この主張を用いると,
\(\displaystyle{ left| \int_{I} \lim_{n to \infty} f(x)dx right| \leq \int_{I} \lim_{n to \infty} |f(x)| dx < \infty}\)
という計算が出来ます.この式は,\(|f|\)だけでなく,\(f\)自体も積分したら有限である事を主張しています.定理の二つ目の主張はこの有限の値が具体的にいくつかという事を計算する為の具体的な方法を示しています.
この定理の仮定から暗に主張されている事
次に定理の仮定について考えてみます.この定理を使う為の条件としていろいろと仮定していますが,実はこれら仮定したことで,定理の結論以外の事も暗に示されています.
例えば,定理の仮定には書かれていませんが,すべての\(n\)について,\(f_{n}\)は可積分(つまり,\(\displaystyle{\int_{I} f_{n}(x)dx < \infty} \))でなければなりません.これを示してみましょう.
\(n\)を一つ固定します.定理の仮定から,すべての\(x\)について,\(|f_{n}(x)| < g(x)\)となるような\(I\)上の連続関数\(g\)があります.積分するという操作によって大小関係は変わらないので,これを\(I\)上で積分すると,
\(\displaystyle{ \int_{I} |f_{n}(x)| dx \leq \int_{I} g(x) dx}\)
となります.定理の仮定から右辺は有限の値なので.それより小さい左辺も有限の値です.
「可積分」 という条件について
区間が無限に伸びる可能性が出た為に,積分した結果が無限になる可能性が出てきました.そのような可能性をうまく統制する為に,「積分した結果は有限でなければならない」という形の条件が何カ所かに出てきます.
先ほどのルベーグの収束定理1でこのような条件は出てこなかったのは,この積分して有限になるという条件は自動的に満たされるからです.その事を次の定理を使って証明してみましょう.
「最大値」という時には\(\infty\)を取らないのが一般的だと思いますが,その事を強調する為に,「有限の」という言葉を付け加えています.この定理を用いると,\(f\)の可積分性が示されます:\(f\)を\([a, b]\)上の連続関数とすると,この定理から\(f\)は最大値\(M (< \infty)\)を取ります.従って,
\(\displaystyle{ \int_{I} |f(x)| dx \leq \int_{I} M dx = M(b-a) < \infty }\)
となり,有限に関する条件は自動的に満たされる事が分かります.
2つの定理の間の関係
収束定理として2つ挙げましたが,2つ目の定理は1つ目の定理を完全に含んでいます.従って,内容的には2つ目の定理さえ知っていれば,1つ目の定理は新しい事は何も含んでいません.
前述の反例達の再考
先ほど区間がルベーグ収束定理1の場合で反例を2つ挙げました.これらは積分と極限が交換しないので,この新しい定理を適用できてしまっては困ります(もし適用できたとしたら積分と極限は交換できなければなりません).
ということは2つ目の定理の仮定も満たしていない事が分かります.結論を言うと,反例1も反例2も条件を満たすような\(g\)を作る事が出来ません.気になる方は証明してみてください.
2つ目の定理の反例
せっかくよりより広い範囲に定理が使えるようになったので,この定理についての反例を考えてみます.状況設定は次の通りです.
- \(I = (-\infty, \infty).\)
- \(f_{n}(x) = \displaystyle{ \frac{1}{n} \cos x }.\)
- \(f(x) = 0.\)
任意の\(x in \mathbb{R} \)について,\(\displaystyle{ \lim_{n \to \infty} f_{n} (x) = 0 }\)
なので,\(f_{n}\)は\(f\)に各点収束しています.しかし,\(f_{n}\)自体は全区間に渡っての積分をする事はできません.つまり,ルベーグの収束定理の結論の式の左辺をそもそも立式することができません.
連続関数とは限らない場合の収束定理
今まではすべて連続関数の範疇で考えていました.しかし,物理や工学等で出てくる関数は連続関数とは限りません.例えば,矩形波等は収束定理の中に組み込みたいです.連続関数でなかったとしても,せめてリーマン積分ができるならばよしとしたいです.
ルベーグの収束定理の主張の中で扱われている積分はルベーグ積分である事が多く,またルベーグの収束定理はその範疇で扱われる事が多いです.リーマン積分とルベーグ積分の概念は一部で重なります.
残念ながら,この定理は定義域\(I\)が閉区間ではない場合は正しいとは限りません.例えば定義域を\(I = [0, \infty)\)とし,この上の関数\(\displaystyle{f = \frac{\sin x}{x}}\)はリーマン積分(この場合広義リーマン積分)は可能ですが,ルベーグ積分は可能ではありません
では最後に不連続の場合も許容するルベーグの収束定理を紹介します.
まとめ
今回のエントリーでは,極限を取るという操作と積分をとるという操作が交換する為には,どのような条件が必要かという話をしました.