RBFEPとは

近年、タンパク質の立体構造に基づいて有望な低分子化合物を設計するStructure-Based Drug Design (SBDD)の分野では、標的タンパク質に対する化合物の結合能(≒薬理活性)の予測を行う結合自由エネルギー計算が注目を集めています。とくに共通骨格をもつ2つの化合物間の結合自由エネルギーの差(相対結合自由エネルギー; ΔΔG_bind)を計算するRelative Binding Free Energy Perturbation (RBFEP, 図1)の技術の発展は著しく、多くのタンパク質系に対して入力した化合物の結合能を誤差 1.0 kcal/mol 以下の精度で予測可能になりつつあります。この程度の精度があれば、化合物を実際に合成する前に、計算機で合成するべき化合物を絞り込むことが可能になるため、ヒット最適化からリード最適化における創薬研究を大幅に効率化することが可能となります。

一方で、RBFEPは創薬に適用される計算技術の中でも、とくに計算コストが高いことで知られています。RBFEPは分子動力学シミュレーション(Molecular Dynamics Simulation; MD)を応用した技術ですので、その高速な実行にはGraphic Processing Unit (GPU)の利用が不可欠です。RBFEPを実際の創薬現場で活用するとなると、1創薬テーマあたり週に数十〜百の化合物の結合能を予測することが求められ、GPUとしては少なくとも数十機が必要となります。これだけのGPUリソースを確保することは投資面や運用面において大きな課題として残されており、RBFEPの恩恵にあずかれる研究者はまだまだ少ないのが実情となっています。

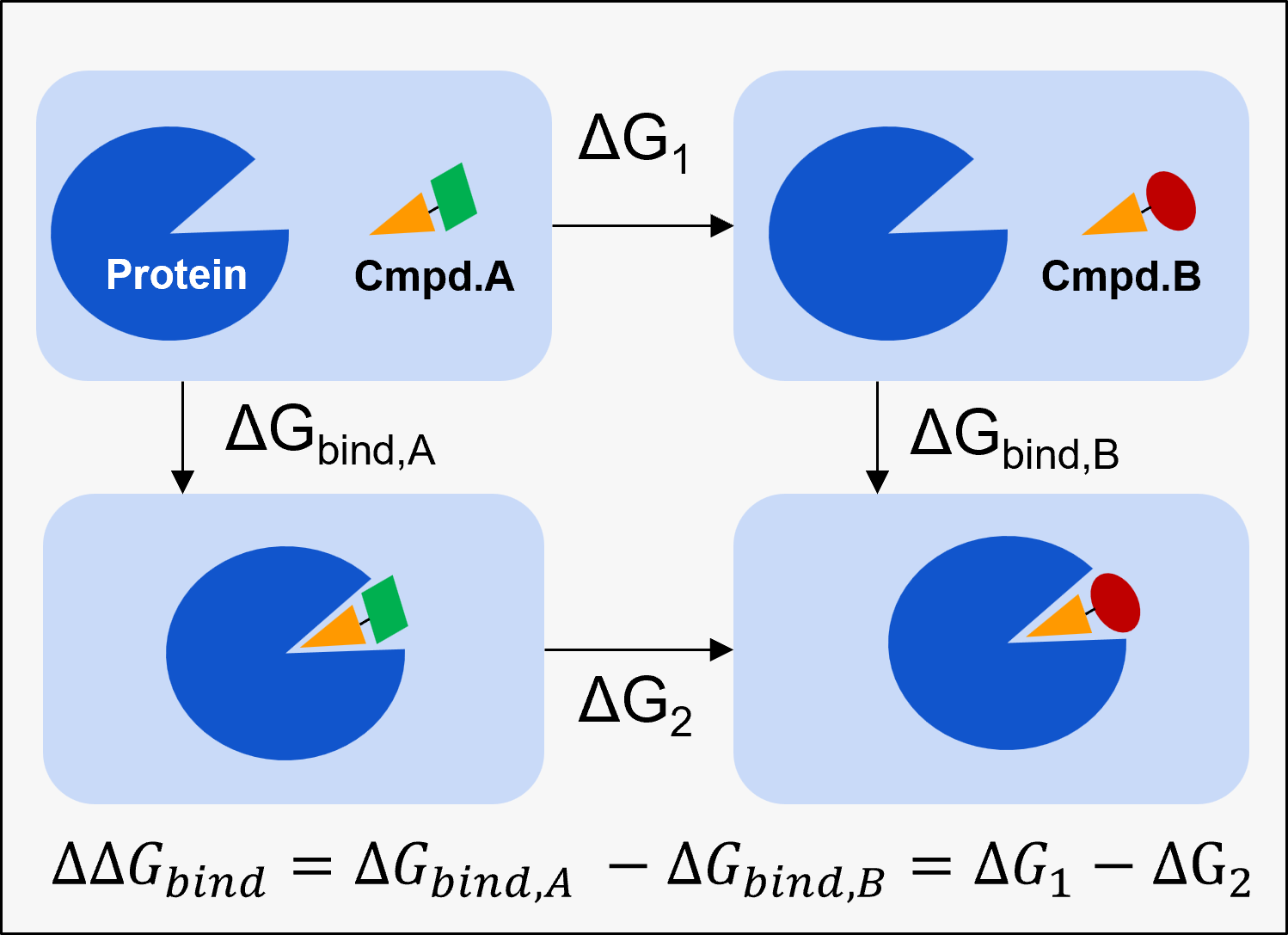
[図1] RBFEPの概要。共通の骨格をもつ化合物Aを化合物Bにアルケミカルに変換する過程の自由エネルギー変化をタンパク質結合状態(ΔG₁)および非結合状態(ΔG₂)で計算することで、化合物Aと化合物Bの結合自由エネルギーの差(ΔΔG_bind)を計算する方法。このΔΔG_bindを多数の化合物ペアで計算した後、各化合物の結合自由エネルギー(ΔG_bind)を推定する。

P-FEP提供開始

さて、このたびPreferred Networks (PFN)では、創薬研究者向けにP-FEPと呼ばれるRBFEPの受託サービスを提供することとなりました。PFNは、GPUを大量に搭載したスーパーコンピューターを保有しており [1]、P-FEPではRBFEPのすべての計算をこの自社クラスタ上で実行します。そのため、お客様には計算機リソースを用意していただくことなく、多量の化合物のRBFEPをいつでも高速に実行していただくことが可能となっております。また、タンパク質系のセットアップ等におきましても弊社の熟練の研究者が代行させていただくことも可能となっており、計算化学に基づいた化合物デザインにご興味のあるメディシナルケミストの方々にもご利用いただきやすいサービスとなっています。

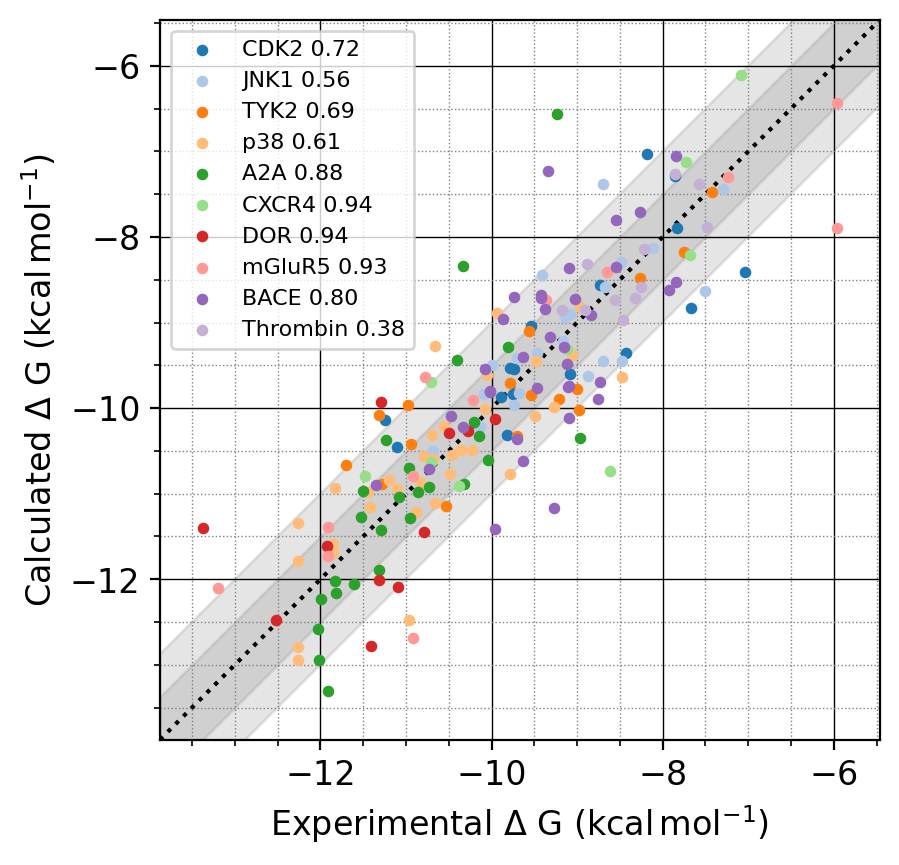
本ブログ記事は、P-FEPの精度や特徴について、その一部を紹介することを目的としています。まずは、RBFEPの精度の指標としてよく使われている公開ベンチマークセット [2-6]に対するP-FEPの精度を紹介いたします。図2は、多くの創薬テーマの標的となっているキナーゼや、膜タンパク質のGPCRを含む10のタンパク質系に対するP-FEPの計算結果を示しています。ΔΔG_bindから推定したΔG_bind (計算値)と実験結果の誤差 (RMSE)はいずれのタンパク質に対しても1.0 kcal/mol以下を示しており、P-FEPは非常に高い精度でΔG_bindを予測可能であることを示しています。

[図2] 10タンパク質に対するP-FEPの計算結果。凡例には標的タンパク質名とΔG_bindの実験値と計算値の誤差を表すRMSE [kcal/mol]を併記した。

続いて、P-FEPの特徴として、精度向上のために取り組んでいるいくつかの試みを紹介したいと思います。まず以下に、P-FEPにおけるΔG_bind計算の手順を示します。

1. 計算したい化合物の3次元構造(結合ポーズ)を用意
2. 各化合物に力場パラメーターを設定
   1. Off-site Charge (Virtual Site)が利用可能
   2. Neural Network Potential (NNP)のひとつであるPreferred Potential (PFP) [7]による力場パラメーターのオーダーメイドが可能
3. アルケミカル変換マップを作成し、ΔΔG_bindを計算する化合物ペアを決定 [8]
4. 各化合物ペアのΔΔG_bindを計算
   1. 化合物間の最大共通部分構造を抽出
   2. タンパク質結合状態および非結合状態で、化合物Aから化合物Bに変換する過程の中間状態を作成
   3. REST2を用いてMDを実行し [9]、各中間状態の平衡状態のトラジェクトリを取得
   4. MBAR法でΔΔG_bindを計算 [10]
5. 全化合物ペアのΔΔG_bindから各化合物のΔG_bindを推定 [11]

上に示しました手順の全体的な流れは一般的なRBFEPと共通していますが、P-FEPではこれらすべての手順において、弊社独自の技術を用いた新規実装もしくは改良を行っており、丁寧な作り込みを行っています。この後に続くセクションでは、手順1と手順2に関連するP-FEPの特徴を簡単に説明させていただきます。

化合物の初期構造(結合ポーズ)の予測

RBFEPでは入力に用いる化合物の3次元初期構造(結合ポーズ)が非常に重要で、最終的に推定されるΔG_bindの精度に大きく影響することが知られています。P-FEPでは、2つの化合物の共通部分構造の判定(手順4-1)に、入力された3次元構造を使用します。ゆえに、間違った3次元構造を初期構造として入力すると、例えば現実世界では空間的に近い位置に存在するべき原子同士が、シミュレーション上では常に遠く離れた位置に配置されてしまうといったことが起きてしまいます。逆も同様です。このような場合の多くでは、手順4-3の平衡状態の達成が困難となってしまい、結果的に不正確なΔΔG_bindおよびΔG_bindの算出に繋がってしまいます。

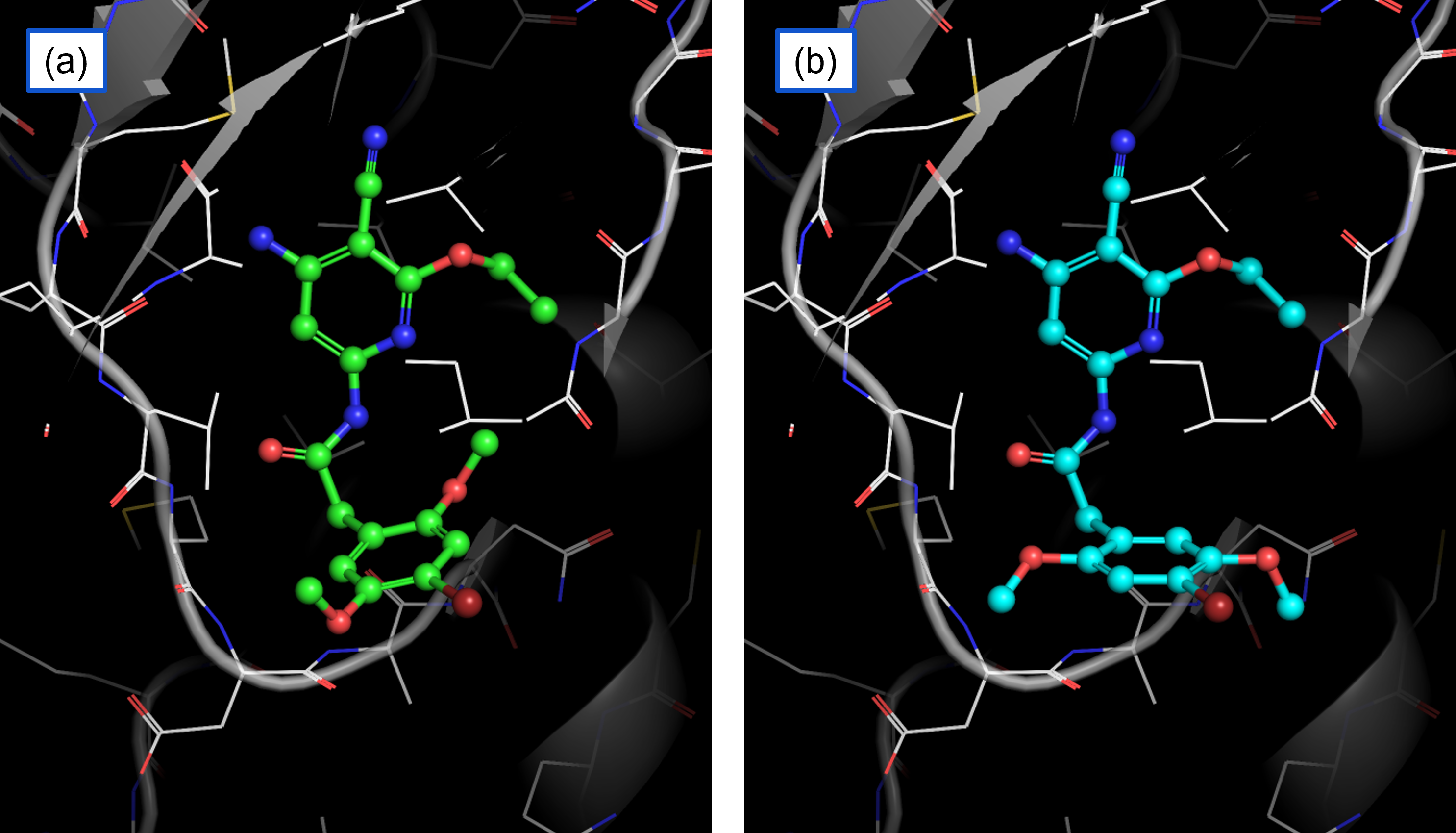
P-FEPでは手順1の際に、分子ドッキングやMDを組み合わせた独自のシミュレーション技術を使用することで、正しい初期構造の生成に努めています。ここではJNK1を用いた一例でその威力を説明します。図3-aはJNK1と化合物17124のX線結晶構造(PDB: 2GMX)を表示したもので、これは公開ベンチマークセット [2]のテンプレートとして使用されている複合体構造になります。まずは、正しい初期構造を使用することの重要性を確認するために、17124のフェニル基部分をあえて反転させた初期構造(図3-b)を用いて、P-FEPを実行しました。その結果を図4-aに示します。その他の化合物の初期構造はデータセットに用意された構造をそのまま使用しました。図4-aで示しているとおり、17124のΔG_bindの予測精度は低く、正しい初期構造を使用することの重要性を示唆する例となっています。

続いて、PFN独自のシミュレーション技術を用いて、すべての化合物の初期構造を生成し直してからΔG_bindを予測した結果を図4-bに示します。化合物17124のΔG_bindを正しく予測できるようになったことに加えて、全体的な予測精度も向上したことがわかりました。生成された結合ポーズも、X線結晶構造(図3-a)と相違ないことが確認できました。

今回の例の場合、図3-aと図3-bにおける17124の相互作用様式を観察してみても、17124のフェニル基上の官能基がタンパク質と明白な相互作用を形成しているようには見えません。これは研究者の手動モデリングや、簡易的な計算化学手法では正しい結合ポーズを予測するのが困難な状況であることを示唆しています。にも関わらず、PFN独自のシミュレーション技術は、短時間で安定な結合ポーズを正しく判定できており、その有用性を示すことができました。

[図3] JNK1に対する17124の結合ポーズ。(a) X線結晶構造(PDB: 2GMX)。(b) 実験のためにフェニル基をあえて反転させた結合ポーズ。

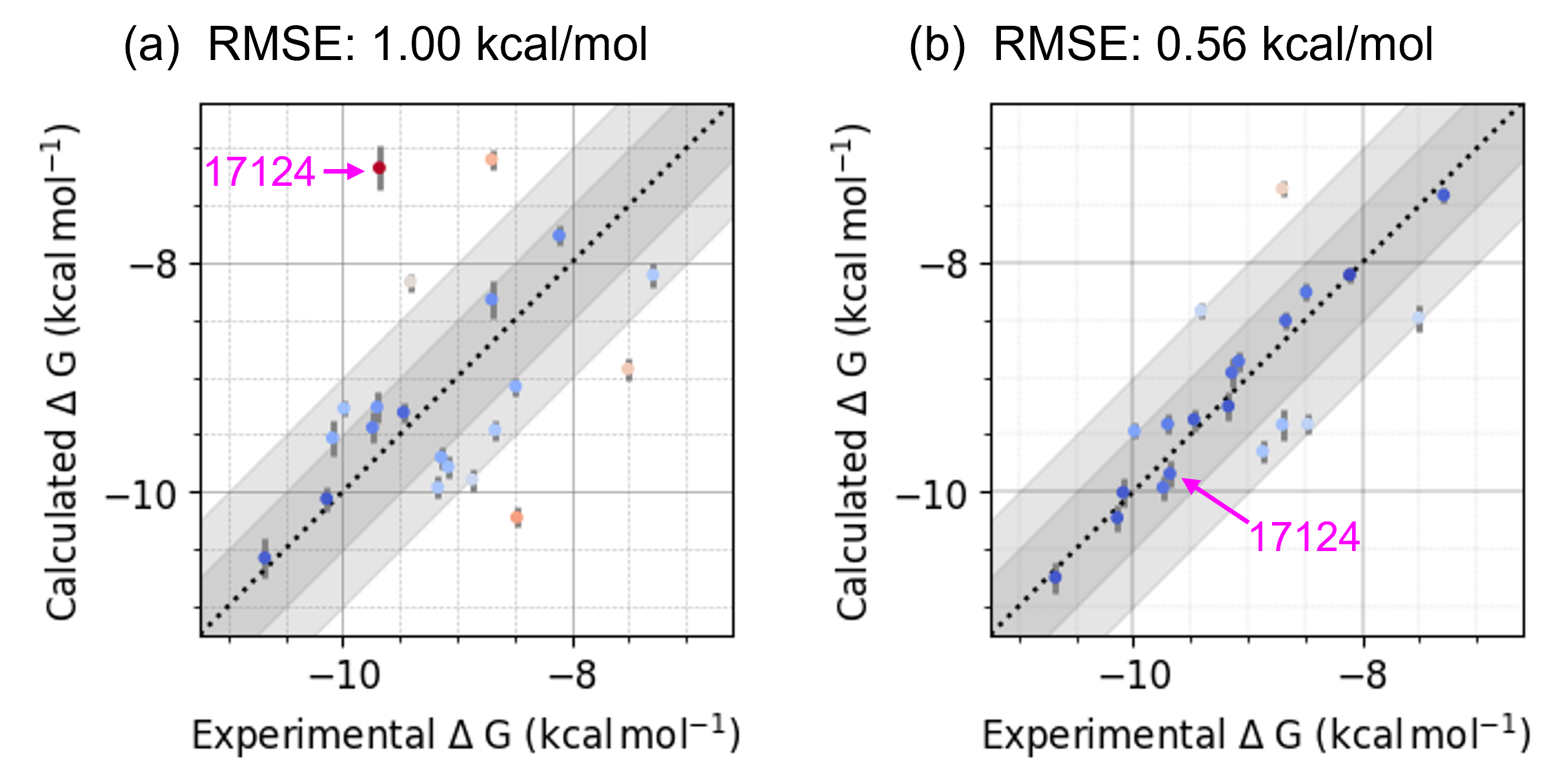
[図4] JNK1に対するP-FEPの計算結果。(a) 化合物の初期構造にデータセットの構造を用いるが、17124のみフェニル基を反転させた構造(図3-a)を使用した場合。 (b) すべての化合物の初期構造を独自のシミュレーション技術により生成した場合。

PFP-distiller: NNPによる力場パラメーターの改良

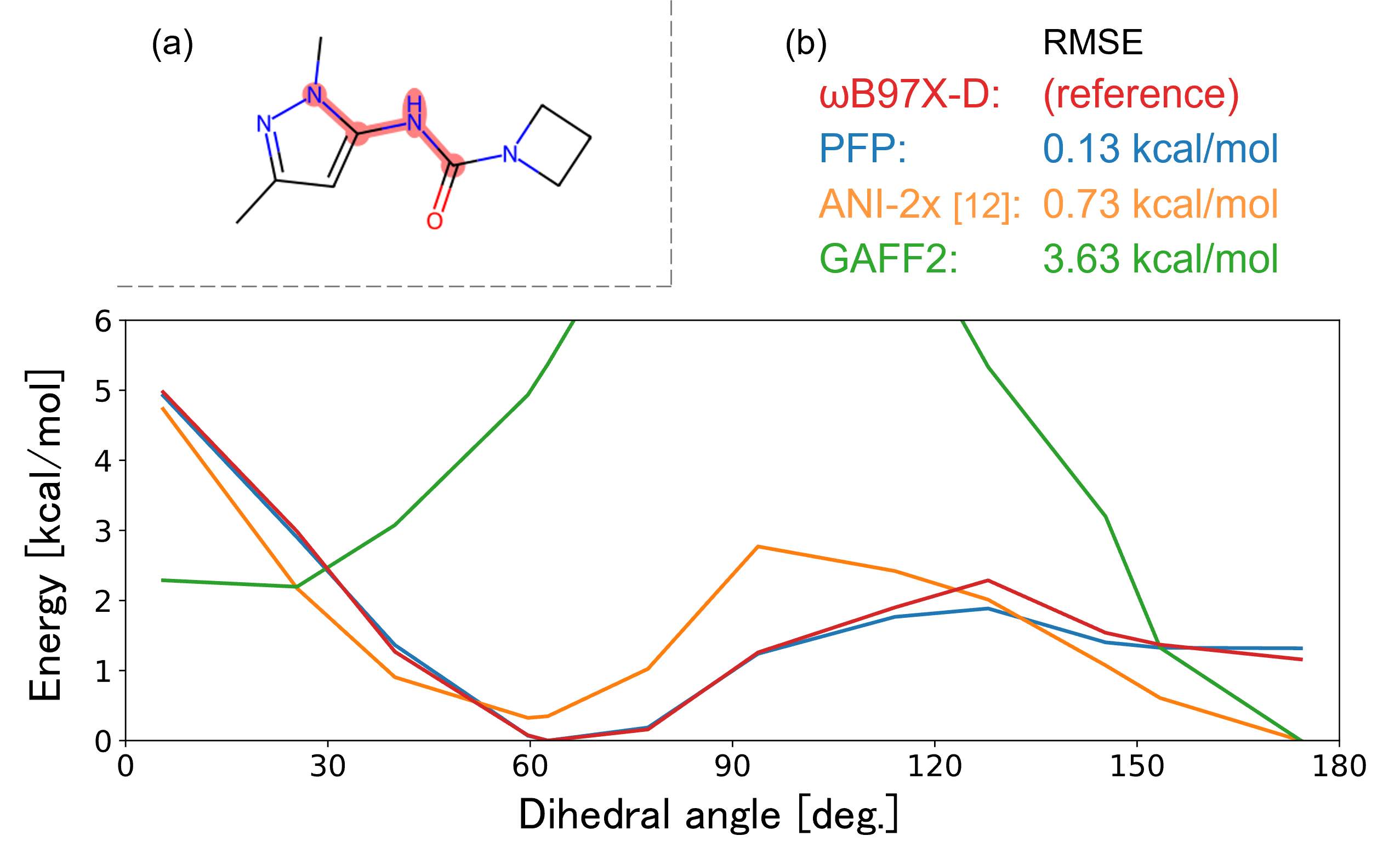
一般的に低分子化合物に使われる力場は、複雑な化合物に対しては精度が不十分であることが知られています。図5に一例として、各種方法の回転可能結合の回転障壁プロットを示します。ここでは低分子化合物用の力場としてGAFF2を、リファレンスとして低分子化合物に対してよく使われる量子化学(QM)計算のωB97X-D法を使用しました。図より、GAFF2とωB97X-D法から計算されるエネルギーは大きく異なることがわかります。このような力場の精度不足は、RBFEPのΔG_bind予測の精度低下の一因として考えられています。

このような問題に対して、精度不足と考えられる部分構造の力場パラメーターをQM計算を用いて新たに作成し、データベース化することで、力場を補完するといった試みが行われています。しかし、どのような場合に新規パラメーターを作成するべきかの判断が非常に難しいことが課題となっています。また、力場パラメーターは部分電荷にも影響されうることから、汎用的なパラメーターは存在しないという考えもあります。以上のことを考慮すると、計算したい化合物ひとつひとつに対して、力場パラメーターをオーダーメイドすることが理想的であると考えられます。しかしQM計算は計算コストが高く、数百配座のエネルギーや力を計算するだけでも長時間を要するため、このようなオーダーメイドのパラメーター作成も現実的とは考えられていませんでした。

[図5] (a) 回転障壁プロットの対象となる化合物と二面角。(b) 各手法の回転障壁。

PFNとENEOS株式会社はNeural Network Potential (NNP)であるPreferred Potential (PFP)を共同開発しています [7, ※]。PFPは、化合物のエネルギーや力をQM計算相当の精度で、かつ非常に短時間に計算できることが特徴で、力場パラメーターのオーダーメイドに適した方法であると考えられます。図5では、PFPが実際にωB97X-D法のエネルギーを他のNNPと比べても、非常によく再現できることを示しています。

P-FEPでは、PFP-distillerと呼ばれる仕組みを用いて、化合物ごとにオーダーメイドした力場パラメーターをRBFEPに使用することができます。PFP-distillerは、PFPで計算した数万の配座のエネルギーと力に合うように、化合物ごとに力場パラメーターを最適化することで高精度な力場パラメーターを作成します。その際、原子核と離れた位置に点電荷を配置するVirtual Siteを使用することも可能となっており、例えばハロゲン属元素のσホール周辺の静電ポテンシャルを精度良く再現することができます。

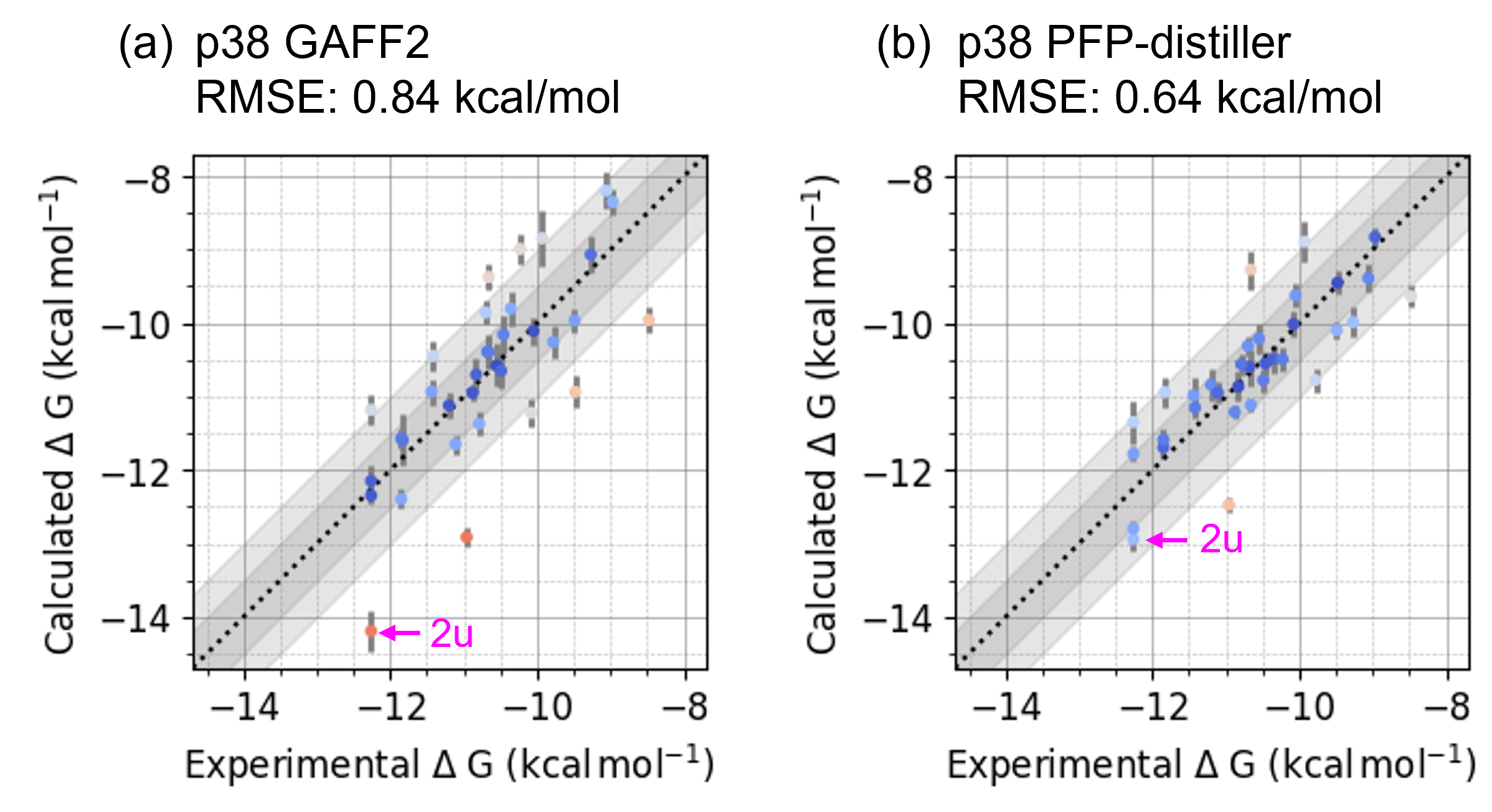
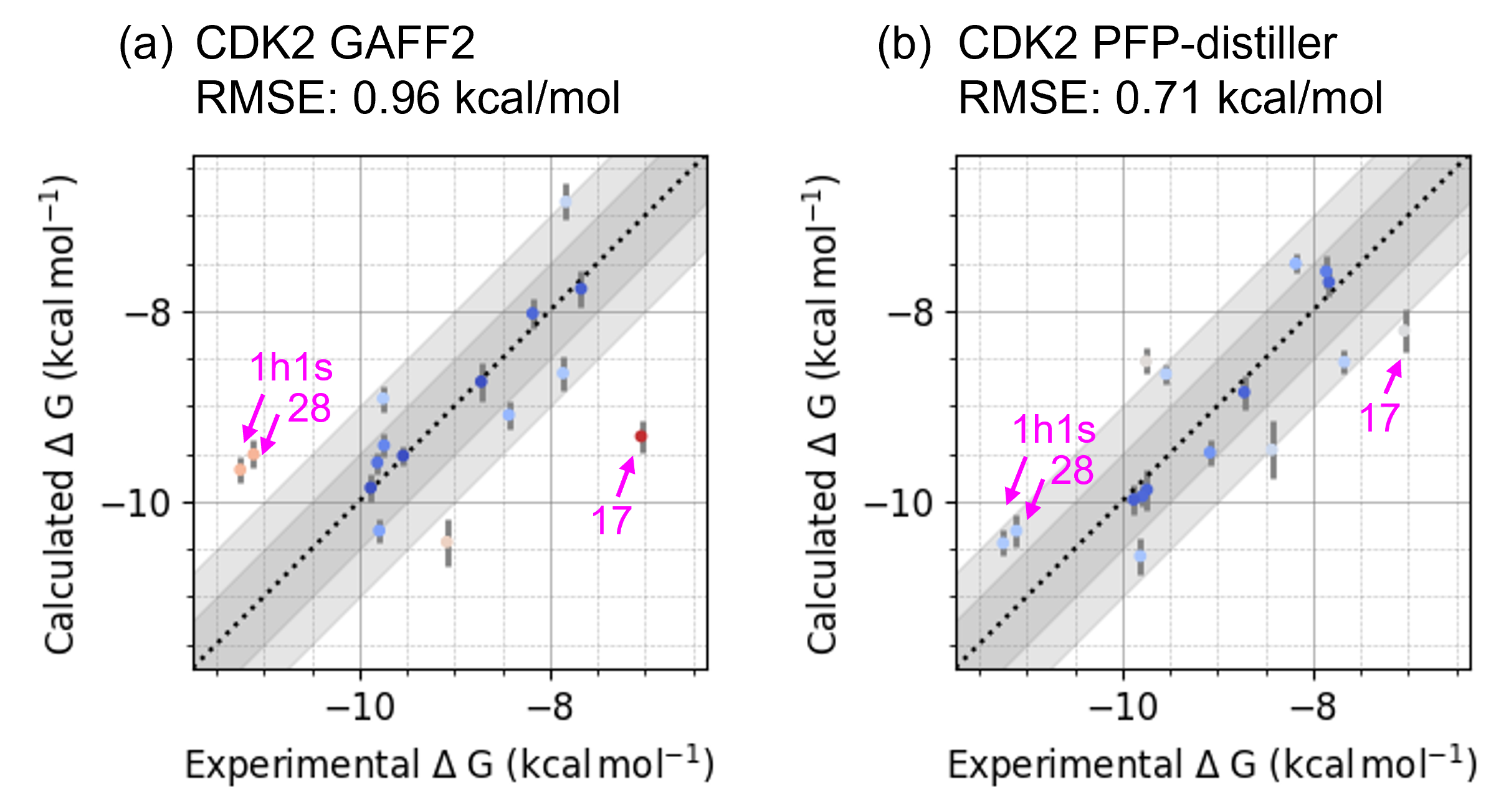
続いて、GAFF2およびPFP-distillerで作成したオーダーメイド力場パラメーターを用いてP-FEPを実行した結果を比較します。図6にはp38に対する結果を、図7にはCDK2に対する結果を示しました。両タンパク質とも、GAFF2を用いた場合でもΔG_bindのRMSEは0.84 kca/mol (図6-a)ならびに0.96 kcal/mol (図7-a)で良好と言えるものの、いくつかのOutlierが存在することが確認できます。

p38において最大のOutlierである化合物2uは、データセットの中で唯一スルホンアミド基を有する化合物です。CDK2データセットでは、化合物1h1sと化合物28のみがスルホンアミド基を有しており、いずれもOutlierであることが確認できます。これらの結果から、GAFF2はスルホンアミド基に対して精度不足であることが示唆されます。CDK2のもう1つのOutlierである化合物17は、データセット中唯一ブロモ基を有した化合物であり、GAFF2ではσホール周辺の静電ポテンシャルの表現が不正確であることが懸念となります。

PFP-distillerを使用した結果では、これら4つのOutlierに対する予測精度はいずれも改善しており、全体的な計算精度の指標であるRMSEも改善していることが確認できます(図6-b、図7-b)。このようにP-FEPでは、QM計算相当の精度を持つポテンシャルを用いて低分子化合物の力場パラメーターをオーダーメイドすることで、精度の高いΔG_bindの予測結果を提供することが可能となっております。

PFP-disitillerはまだ発展途上の技術ですので、引き続き、開発・検証を進め、さらに有用な技術として提供できるように努めています。

※PFPが搭載された汎用原子レベルシミュレータMatlantis™は、材料分野の研究開発向けに(株)Preferred Computational Chemistryが販売とサポートを行っております。

[図6] p38に対するP-FEPの精度。(a) GAFF2を使用した場合。(b) PFP-distillerによるオーダメイド力場パラメーターを使用した場合。

[図7] CDK2に対するP-FEPの精度。(a) GAFF2を使用した場合。(b) PFP-distillerによるオーダメイド力場パラメーターを使用した場合。

タンパク質ごとに条件検討をすることの重要性

これまでにP-FEPの特徴として、RBFEPの精度向上に向けた取り組みを2点紹介しました。しかしながら、計算化学の本当に難しい点は、これらの技術が必ずしもすべてのタンパク質において有用ではなく、各タンパク質や化合物骨格に対して、最適な計算条件が異なるというところにあります。P-FEPでは、大規模に計算を行う前に、10前後の既知化合物を用いて実験条件をもっともよく再現できる計算条件をできる限り探索します。そうすることで、未知の化合物に対する予測精度をできるだけ向上させ、高品質の予測結果を提供することに努めています。

今後の展開

今回、PFNがローンチするサービスはRBFEPを主体としたサービスになりますが、RBFEPは共通骨格をもつ化合物間でしか結合能を比較できないといった制限があるため、創薬研究者の需要を必ずしも満たすものではありません。そこで今後は、任意の化学構造のΔG_bindを計算可能なAbsolute Binding Free Energy Perturbation (ABFEP)のような技術を提供し、RBFEPと組み合わせることで、より広範なニーズに応えることを目標として、現在、実装および検証に注力しております。

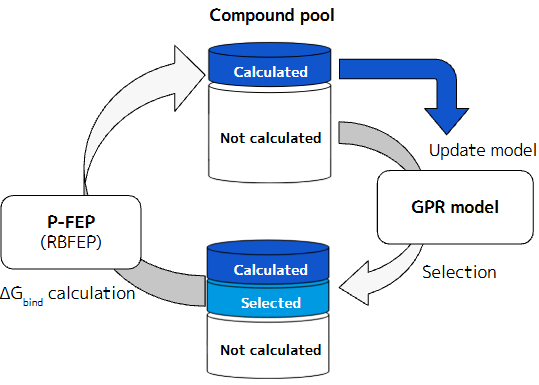
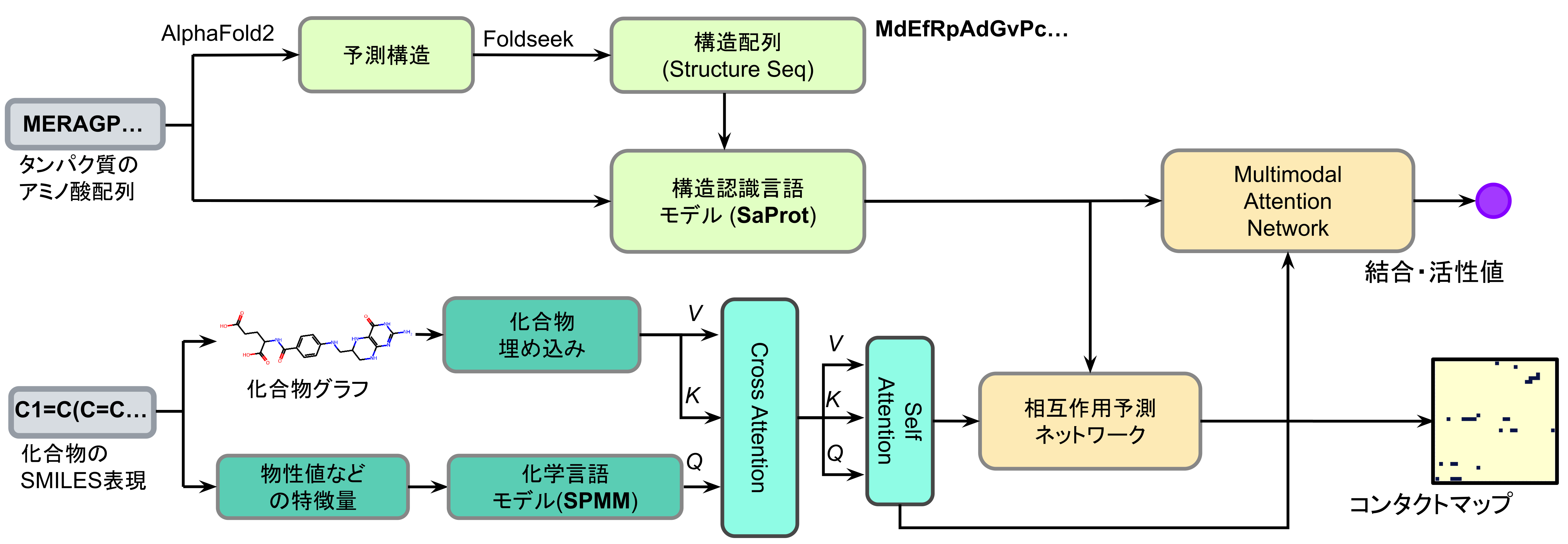
また、強い活性化合物の取得に最短経路でたどり着くためには、やはり人工知能(AI)の活用が有効だと考えています。現在PFNでは、RBFEP(もしくはABFEP)の計算値や薬剤としての望ましい性質(drug-likness)等を学習しながら、次に計算するべき化学構造を提案するAIの技術開発も並行して進めています。

おわりに

P-FEPに興味を持っていただけた方や、今後の案内を希望される方は、弊社ホームページ 「ビジネスに関連するお問い合わせ」、もしくはメール drug-info[=]preferred.jp (アットマークに変換) にて「P-FEPの案内希望」と添えましてご送信いただけますと幸いです。

P-FEPの詳細やその他タンパク質のベンチマークにつきましては、現在作成中のホワイトペーパーでもご確認いただけます。公開しましたら、こちらのブログにてアナウンスさせていただきます。

引き続き、PFNならびにP-FEPにご注目いただけますと幸いです。

References

[1] https://projects.preferred.jp/supercomputers/
[2] Wang L, et al. Accurate and reliable prediction of relative ligand binding potency in prospective drug discovery by way of a modern free-energy calculation protocol and force field. J. Am. Chem. Soc. 2015;137(7):2695-2703.
[3] Schindler CEM, et al. Large-Scale Assessment of Binding Free Energy Calculations in Active Drug Discovery Projects. J. Chem. Inf. Model. 2020;60(11):5457-5474.
[4] Deflorian F, et al. Accurate Prediction of GPCR Ligand Binding Affinity with Free Energy Perturbation. J. Chem. Inf. Model. 2020;60(11):5563-5579.
[5] Lenselink EB, et al. Predicting Binding Affinities for GPCR Ligands Using Free-Energy Perturbation. ACS Omega. 2016;1(2):293-304.
[6] Guo Y, et al. A Benchmark for Accurate GPCR Ligand Binding Affinity Prediction with Free Energy Perturbation. ChemRxiv. 2023. doi:10.26434/chemrxiv-2023-mhp2x
[7] Takamoto S, et al. Towards universal neural network potential for material discovery applicable to arbitrary combination of 45 elements. Nat. Commun. 2022;13(1):2991.
[8] Liu S, et al. Lead optimization mapper: automating free energy calculations for lead optimization. J. Comput. Aided Mol. Des. 2013;27(9):755-770.
[9] Wang L, et al. Replica exchange with solute scaling: a more efficient version of replica exchange with solute tempering(REST2). J. Phys. Chem. B. 2011;115(30):9431-9438.
[10] Shirts MR, et al. Statistically optimal analysis of samples from multiple equilibrium states. J. Chem. Phys. 2008;129(12):124105.
[11] Xu H. Optimal Measurement Network of Pairwise Differences. J. Chem. Inf. Model. 2019;59(11):4720-4728.
[12] Devereux C, et al. Extending the Applicability of the ANI Deep Learning Molecular Potential to Sulfur and Halogens. J. Chem. Theory Comput. 2020;16(7):4192-4202.