岡野原です。
ブログの更新がとまっていましたが、また少しずつ更新してきたいと思います。
今回はtrie(トライ)の最近の話をしたいと思います。
trieはキー集合を扱うためのデータ構造の一種です。例えば、単語集合からなる辞書であったり、クロールしたURL情報を扱ったり、最近だと、KVS(Key Value Store)のようにキーを介してデータを保存、読み込みをしたりと様々な場面で利用されます。
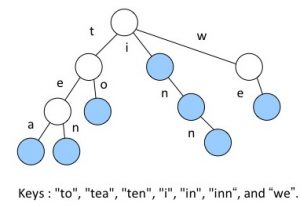
trieは図にあるように、木構造で各枝に文字が付随しており、根から葉へのパス上に付随する文字をつなげた文字が各キーに対応します。
同じようにキー集合を格納するデータ構造としてハッシュを利用する方法があります。キーからハッシュ値を計算し、その場所に文字列へのポインタを格納しておくデータ構造です。ハッシュを利用した場合とtrieを利用した場合の一番の大きな違いは、trieの場合だと、ある文字列から始まるキーを全て列挙する、いわゆる接頭辞探索ができることです。例えば”te”で始まる文字列を網羅的に調べることができます。木をたどって、”te”の下にある葉を全て列挙するだけです。hashはこの操作を効率的に行うことはできません。同様に辞書式順序でxよりも大きく、yよりも小さいキーを全て列挙するといったこともtrieは効率的に実現できますが、hashだとできません。
trieの大きな問題点として、木構造を格納する必要があり作業領域量が大きいという問題がありました。そのまま木構造を素直にポインタベースで実装してしまうと、元のキー集合に対しその数倍の作業領域量を必要とする場合も少なくありません。
この問題は簡潔木を利用することで解決できます。このアイディアを実装したものが
tx,
uxなどです。私もお世話になっているGoogle IMEもtxのクローンであるrxを利用することで大規模辞書を効率的に管理しています。
木構造を圧縮すると、元のキーをそのまま格納するよりも小さく格納できるようになり、データ圧縮としても利用することができます。trieでは文字列の先頭部分(接頭辞、prefixと呼びます)を一つのパスとして表現することができるためです。しかも、通常のデータ圧縮とは違って、データ全体を復元しなくてもあるキーのみを復元するということができます。
簡潔木を利用したtrieについての情報は既にある程度広まってきているので、今回は簡潔木を利用しないtrieの最新情報についていくつか紹介します。
XBWを利用したtrie
[1] “Structuring labeld trees for optimal succinctness, and beyond”, P. Ferragina, and et. al. FOCS 2005
[2] “Succinct Dictionary Matching With No Slowdown”, D. Belazzougui, CPM 2010
[3] “Faster Compressed Dictionary Matching”, W. K. Hon, and et. al. SPIRE 2010
ラベル付木に対する簡潔データ構造であるxbwは[1]により最初に紹介されました。その後[2], [3]の論文で、さらにxbwはシンプルになり高速化されています。
xbwについて簡単に説明します。
ノードから根に向かって辿った時の文字列をつなげた文字を、そのノードのreverse prefix pathと呼ぶことにします。次に全ノードをreverse prefix pathの辞書式順序でソートします。複数のノードが同じreverse prefix pathを持つ場合がありますが(trieの場合は無いが)、その時は木中の幅優先探索の順序順で順番を決定するとします。最後に各ノードの子に付随する文字をその順に格納します。これがxbwです。先ほどのtrieの場合の例を以下の図に示します。列reverse prefix pathは各ノードから根に向かうパスであり、末尾は特殊文字$がつけてあります。この$は他のどの文字よりも小さいとします。列childrenにそれぞれのノードに対応する子に付随する文字を格納します。ここで#とあるのはそこが終端ノードであることを示しています。この#は他のどの文字よりも大きいとします。children内部での順序は関係ありませんので集合で表すことにします。例えばchildren[1] = {t, i, w}, children[3] = {a, n}です。
結論を先に言うと、このchildrenの列だけを使って先程のtrieを完全に表現することができます(reverse prefix pathはいらない)。
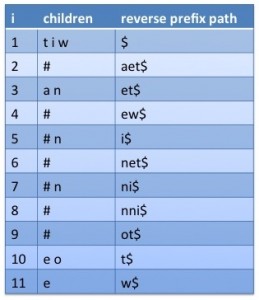
実際に節点をchildrenの情報だけを使って辿ってみましょう。
rank(i, c)をchildren[1…i-1]中に含まれる文字cの出現数と定義します。また、C(c)を全てのchildren中で”c”より小さい文字の出現個数とします。例えばこの図の例ですとですとC(a)=0, C(e)=2, C(i)=4…となります。
まず、図中の根のノードに着目してみます。先程の表では、i=1となります。ここからラベル”t”を辿った場合、次に行くべきノードのreverse prefix pathは”t$”です。このノードは”t”で始まるreverse prefix pathを持つノードの中では最小のはずです。よって”t$”を持つノードはC(t)+1 = 10となります。
では、次にこのノードからラベル”e”を辿るとすると、その節点は”et$”をreverse prefix pathとして持つはずです。”e”で始まるreverse prefix pathを持つノードの数は、children[1…9]の中で”e”を持っている数に一致します。なので、”et$”に対応するノードの番号はC(e)+rank(10, e)+1=3となります。
このように、現在iの位置にいる時に文字cを辿った先のノード番号は
C(c)+rank(i, c)+1
として求められます。C(i, c)+1は文字”c”から始まるreverse prefix pathを持つノードが始まる添字番号であり、rank(i, c)はその中での順番です。
既にお気づきの方も多いと思いますが、これはBWT (Burrows Wheeler Transform, BlockSorting) におけるLF-mappingと同じ考えです。bwt(block sorting)は一本鎖のパスからなる木に対するxbwであり、xbwはbwtの自然な拡張になっています。
さて、このchildrenのテーブルをどのように効率的に格納し、rankを高速に求められるかが問題です。BWTの場合はここが文字列になっていたため、wavelet treeを利用することができました。今回は各位置に複数の文字が存在します。[1]では、ビットベクターと組み合わせることによって、集合を文字列にしてしまい、文字列に対するrank操作の問題に還元しました。[2], [3]では、各文字ごとに、転置ファイルのようにその位置に文字cが出現したかどうかをbit vectorで記録し、bit vectorに対するrank操作としてこれを実現します。どちらも、trieに対するk次経験エントロピーに漸近するサイズで格納できるということが示されています。
さらに、[3]では、このxbwを利用してAC法が実現できることが示されています。
木を潰したtrie
[4] “On searching compressed string collections cache-obliviously”, P. Ferragina, and. et. al. PODS 2008
もう一つ面白いtrieがFerraginaらによって提案されています。
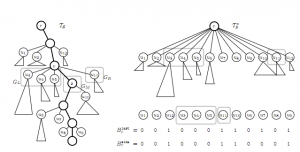
論文にはcache-obliviouslyとありますが、注目すべきはcentroid path decompositionです。従来のtrieは遷移するノード数分だけランダムアクセスが発生しており問題になっていました。特にデータをディスクなどに格納している場合、アクセス回数が操作時間に直結するために問題になります。centroid path decompositionは元々の木を縦方向にぐしゃっとつぶします。
イメージだけでも掴んでもらうために、図を論文から借りてきました。左側の元のtrieの太い線に対応するpathをぐしゃっと一つのノードに潰します。このpathの付随するノードは、このpathの左上から順に右上まで反時計回りの順に大小関係が決まります。そのノードにはheavy pathのラベル列と、そのパスから分岐しているノードが何文字目からどのどの文字で分岐しているかの情報を記録しておきます。この情報により潰した後でも木を辿ることができます。
実際どのようにして潰すpathを決めるかについて説明します。
各ノードについて、その子の中で、最も子孫の葉の数が多い子を、そのノードのheavy childと呼びます。次に、各ノードについて、そのノードから葉までheavy childrenのみを辿っていくpathをheavy pathと呼びます。これを利用したcentroid path decompositionは次のように実行されます。まず最初に根に対応するheavy pathをたどってそのpathを一つのノードに潰します。次にそのpathから分岐して伸びている各ノードについて再帰的に同じようにheavy pathを辿って、そのpathを一つのノードに潰すというのを繰り返します。
この操作により、キーの種類数がK、文字種類数がSの時、木の高さは高々 O(log K)個になり、平均して O(log K / log S)個になります。どんなに高い木でもその順序関係を損なうことなく、木の高さを減らすことができ、アクセス回数を減らすことができます。
各節点での分岐数は増えるため、各節点での計算量は増えますが、アクセス回数が減らせることによりメリットは大きい場合が多いです。
この木に対する簡潔データ構造も論文中に提案されています。
Weak Prefix Search
[5] “Fast prefix search in little space, with applications”, D. Belazzougui, and et. al. ESA 2010
最後に紹介するのがweak prefix searchをサポートしたtrieです。
クエリ文字列pに対し、そのクエリ文字列が辞書中のどれかのキーの接頭辞である場合、そのキーの辞書中の辞書式順序の順位を返す操作をweak prefix searchと呼びます。
もし、クエリ文字列が辞書中のどれかのキーの接頭辞で無い場合、結果は保証せずランダムになります。
よって、weak prefix searchはbloom filterのようにone sided errorを許したデータ構造です。例えば、キー集合が{abc, abef, bcde}の時、abcに対しては1, abeを入力したら2、abcdeならランダムな値が返ってきます。
これまでもweak prefix searchを備えたデータ構造はString B-tree (blind trie)などがこうした機能を有していました。
weak prefix searchは従来のtrieよりも弱い操作です(従来のtrieであれば、無い場合は無いと返すことができる)が、その分作業領域量は少なく抑えることができます。この論文では、
この問題を解くために必要なデータ構造は、従来のキーを格納するよりはるかに少ない作業領域量だけあればよいことを示しました。具体的にはキーの数がK、キーの平均長がLの時、必要な作業領域料はO(K log L)ビットになります。従来だとK Lビット だったのと比べると大きな違いです。
この論文ではz-fast trieを改良したHollow z-fast prefix trieとrange locatorを組み合わせてweak prefix searchを実現します。2-fattest numberなどいろいろ面白いアイディアを利用しています。
最後に
これまで話してきたtrieは実はいずれも動的なキーの追加・削除をサポートせず、前もって与えられたキー集合を扱っていました。
キーの追加・削除をサポートした上で、データをコンパクトに保ちつつ、高速な操作を実現するようなtrieは実現できるのか? これについてはまた紹介します。